
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЯЗКОСТИ ЖИДКОСТИ
РОССИЙСКОЙ ФЕДЕРАЦИИ МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ (МИИТ) _____________________________________________________________ Кафедра «Физика-2»
Утверждено редакционно-издательским советом университета
МЕТОДИЧЕСКИЕ УКАЗАНИЯ к лабораторным работам по дисциплине «Физика»
Работы 7, 11, 12, 80, 82
Под редакцией В.А. КОЗЛОВА Москва - 2005
УДК 537.8 М-54
Методические указания к лабораторным работам по дисциплине «Физика». Работы 7, 11, 12, 80, 82 // Под общ. ред. В.А. Козлова. - М.: МИИТ, 2005. - 44 с.
Методические указания содержат описания лабораторных работ по общему курсу физики, предназначенных для студентов первого и второго курсов всех специальностей. Выполнение работы № 80 планируется в порядке УИРС.
© Московский государственный университет путей сообщения (МИИТ), РАБОТА №7
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЯЗКОСТИ ЖИДКОСТИ
Цель работы: экспериментальное определение коэффициента вязкости (коэффициента внутреннего трения) жидкости по методу Стокса. Приборы и принадлежности: стеклянный цилиндрический сосуд с вязкой жидкостью (с глицерином, касторовым или вазелиновым маслом); мелкие шарики из твердого материала (свинца, стали, стекла); микрометр; секундомер; масштабная линейка.
Введение
Вязкость (внутреннее трение) - свойство текучих тел (жидкостей и газов)оказывать сопротивление перемещению одной их части относительно другой. Она оказывает существенное влияние на протекание многих процессов и ее необходимо учитывать при решении практических задач в различных областях науки и техники: гидро-, аэродинамике, гидравлике, механике трущихся поверхностей (рельс - колесо) и т. д.
Возникновение сопротивления, обусловленное вязкостью, поясним на следующем примере. Представим себе две пластины А и В (рис. 1), пространство между которыми заполнено жидкостью. Пластина В под действием тангенциальной (касательной) силы F движется с постоянной скоростью, пластина А - неподвижна. Слой жидкости, ближайший к пластине В, как бы «прилипает» к ней и движется с той же скоростью, а слой, непосредственно прилегающий к пластине А, - неподвижен. Мысленно разобьем жидкость на плоско-параллельные слои, перемещающиеся с различными скоростями. На рис.1 показана зависимость скорости слоя u(z) от расстояния z до пластины А. Рассечем мысленно жидкость, заключенную между пластинами А и В, на две части площадкой S, параллельной скорости течения жидкости. Молекулы, находящиеся справа от S, обладают большей скоростью, а следовательно и большим импульсом, чем слева. Переходя из пространства BS в AS, молекулы передают часть своего упорядоченного импульса молекулам, с которыми они сталкиваются в левой части (AS). Аналогично, более медленные молекулы, попадая из левой части (АS) в правую, при столкновении отнимают часть упорядоченного импульса у молекул, расположенных в правой части (BS). В итоге жидкость в правой части испытывает как бы тормозящую силу, направленную против скорости u. Таким образом можно объяснить возникновение сил внутреннего трения. Для пояснения этого факта некоторые авторы проводят следующую аналогию. Две железнодорожные платформы движутся по параллельным рельсам с различными скоростями. Грузчики, находящиеся на платформах, перебрасывают мешки с песком со своей платформы на соседнюю. Ясно, что в результате этого быстрее движущаяся платформа будет тормозиться, а медленнее движущаяся - ускоряться. Основной закон вязкого трения был установлен И. Ньютоном:
где F - тангенциальная сила, вызывающая сдвиг слоев жидкости друг относительно друга, S - площадь слоя, по которому происходит сдвиг, h - коэффициент вязкости (внутреннего трения) жидкости.
Согласно формуле (1), h - коэффициент вязкости жидкости численно равен тангенциальной силе, приходящейся на единицу площади, необходимой для поддержания разности скоростей равной единице, между двумя параллельными слоями жидкости, расстояние между которыми равно единице. В СИ h измеряется в Па× с (в СГС - пуаз). В условиях установившегося ламинарного течения при неизменной температуре T коэффициент вязкости - постоянная величина, независящая от градиента скорости. Коэффициент вязкости имеет различные значения для разных жидкостей. Так, например, h глицерина (при температуре t = +20°C) в 1, 5 тыс. раз больше, чем у воды. Для данной жидкости коэффициент h зависит от параметров, характеризующих ее внутреннее состояние, и в первую очередь от температуры, понижаясь с ростом Т. Так, вязкость воды при изменении температуры от 0°C до +100°C уменьшается от 1, 8× 10-3 до 2, 8× 10-4 Па× с. Особенно сильно зависит от температуры вязкость масел; так, например, вязкость касторового масла при повышении температуры от +18°С до +40°С падает почти в четыре раза. Коэффициент внутреннего трения жидкости может быть найден путем измерения силы трения, возникающей при падении твердого тела (например, шарика) в этой жидкости. Различие скоростей слоев жидкости возникает потому, что в результате взаимного притяжения между частицами жидкости и падающего шарика ближайший к нему слой движется с его же скоростью, а остальные - со все уменьшающейся u. Слой жидкости, примыкающий к стенкам сосуда, имеет скорость, равную нулю. Величину силы трения можно определить следующим образом. На твердый шарик, падающий в жидкости, действует три силы: - Сила тяжести P, направленная вертикально вниз и равная P = где r - радиус шарика; r1- плотность материала шарика при данной температуре; g - ускорение свободного падения.
- Подъемная сила Архимеда FA, направленная вертикально вверх и равная весу жидкости, вытесненной шариком, FA= (здесь r2 - плотность жидкости при данной температуре).
- Сила трения Fтр, направленная в сторону, обратную скорости движения (в нашем случае вертикально вверх), и пропорциональная при малых скоростях величине скорости. Как показал Стокс, эта сила при движении твердого тела, имеющего шаровую форму, равна Fтр = 6phu, (4) где u- скорость движения шарика; h - искомый коэффициент внутреннего трения.
F = P - FА- Fтр.
Силы P и FА постоянны, а Fтр растет с увеличением скорости шарика. Это приводит к тому, что равнодействующая данных сил будет уменьшаться до тех пор, пока не станет равной нулю:
F = P - FА- Fтр = 0.(5)
Начиная с этого момента, шарик будет двигаться равномерно. Подставляя значения действующих сил, а также формулы (2), (3) и (4) в выражение (5), получим условие равномерности движения шарика в виде
откуда может быть определено значение h. Подставляя в это уравнение скорость установившегося равномерного движения u = l¤t (здесь l - путь, который проходит шарик за время t) и учитывая, что диаметр шарика d = 2r, получаем окончательное выражение для расчета коэффициента внутреннего трения жидкости: Порядок выполнения работы Прибор, как было сказано выше, представляет собой вертикальный стеклянный цилиндр, наполненный исследуемой жидкостью. На цилиндре снаружи имеются две метки (кольца) в верхней и нижней частях. Эти метки определяют некоторый участок пути равномерно движущегося шарика (рис. 2). Верхняя метка должна быть ниже уровня жидкости на 20-25 см, чтобы шарик, подходя к метке, уже двигался равномерно. Шарики надо опускать ближе к оси цилиндра. Перед опусканием шариков в жидкость следует определить их размеры. Ввиду того, что шарики далеко не идеальной формы, с целью уменьшения ошибки измерения диаметр каждого из них измеряется микрометром не менее пяти раз в различных направлениях. Все результаты измерений записываются в таблицу. Затем каждый шарик бросают в жидкость и измеряют время t, за которое он проходит путь l между метками в сосуде. Для измерения времени служит секундомер, который включается в момент прохождения шариком верхней метки и выключается в момент прохождения шариком нижней метки. Длина пути, то есть расстояние между метками измеряется при помощи масштабной линейки. Опыт необходимо провести не менее чем с пятью разными шариками и вычислить среднее арифметическое значение коэффициента внутреннего трения жидкости hср. Значения плотностей материалов шариков и жидкости берутся из справочных таблиц. Результаты всех измерений и вычислений заносятся в таблицу с указанием системы единиц и размерностей.
Таблица
МЕТОДОМ КЛЕМАНА - ДЕЗОРМА Цель работы. Определение величины отношения теплоемкости воздуха при постоянном давлении к теплоемкости при постоянном объеме. Приборы и принадлежности. Стеклянный (или металлический) баллон, водяной манометр, насос (ручной или электрический в металлическом баллоне). Введение
Первый закон термодинамики утверждает, что количество теплоты DQ, сообщенное газу, расходуется на изменение внутренней энергии газа DU и на работу А, совершаемую газом:
DQ =DU + A.
Теплоемкостью газа называется величина равная количеству теплоты, необходимой для нагревания данной массы газа на один кельвин.
С = lim DQ/DT = dQ/dT. DT®0 Теплоемкость единицы массы газа называется удельной теплоем-костью. Теплоемкость одного моля называется молярной теплоемкостью. Приращение внутренней энергии идеального газаDU, при изменении температуры DТ, определяется выражением:
DU = m /m ´ i /2´ R DT,
где i - число степеней свободы, т.е. число независимых параметров определяющих положение и ориентацию молекулы в пространстве, m - молярная масса газа. Число степеней свободы можно вычислить по формуле
i = 3N - К,
где N – количество атомов образующих молекулу, а К – число жестких связей между этими атомами. При постоянном объеме А = 0. В этом случае DQ = DU. Теплоемкость газа при постоянном объеме Cv=
Работа газа при постоянном давлении
A = p ´ DV = m /m ´ R DT.
Таким образом, теплоемкость газа при постоянном давлении Cp= m /m ´ (i /2 ´ R + R).
Отношение теплоемкостей для данной массы идеального газа зависит от числа атомов в молекуле и определяется числом степеней свободы.
g = Cp/ Cv= ( i + 2) / i .(1)
Приведенная формула верна и для смеси идеальных газов с одинаковым числом степеней свободы.
Порядок выполнения работы
В опыте исследуемым газом является воздух. В начале опыта при закрытом кране надо подкачивать воздух в баллон до тех пор пока разность уровней в коленах манометра не будет равна 25 - 30 см. Через некоторое время (около 2 – 3 минут), когда температура воздуха в баллоне сравняется с температурой окружающей среды, по манометру определяется избыточное давление Dр1 (Dh1пропорционально Dр1). Оно отсчитывается по разности уровней Dh1 в коленах манометра. Газ занимает состояние 1. Затем кран открывают, соединяя баллон с атмосферой и, дождавшись, когда воздух перестанет выходить из баллона, закрывают. (На установке с металлическим баллоном для выхода воздуха из баллона нажимают клапан, помеченный буквой К, а после выхода газа из баллона клапан отпускают). Давление в баллоне упадет до атмосферного, и температура несколько понизится. Через некоторое время (около 2 – 3 минут) благодаря теплообмену температура в баллоне повышается до комнатной. В связи с этим давление в баллоне повысится и установится постоянным. В этот момент надо измерить разность уровней Dh2. Полученные показания Dh1и Dh2занести в таблицу. Весь опыт повторить десять раз.
Таблица
Обработка результатов измерений
Вычислите g по формуле (5), после чего оцените среднее значение < g>: < g > = ( и величину S S =
где n - число измерений. Результаты вычислений представьте в виде:
g = < g > ± Sa
(здесь a - коэффициент Стьюдента). Значение доверительной вероятности выбрать равной 0, 9. Оцените относительную погрешность вычисления g:
dg =(Sa /< g > ) ´ 100 %.
Значение < g > сравните с теоретическим, вычисленным по формуле (1), предполагая, что воздух является смесью двухатомных идеальных газов.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Запишите первый закон термодинамики. 2. Запишите формулу для расчета изменения внутренней энергии идеального газа. 3. Выведите выражения для молярной и удельной теплоемкости идеального газа при постоянном объеме и при постоянном давлении. 4. Рассчитайте молярные теплоемкости при постоянном объеме и при постоянном давлении для одноатомного и многоатомного идеальных газов. 5. Какой процесс называется адиабатическим? Что происходит с температурой газа при адиабатическом расширении и при адиабатическом сжатии и почему? 6. Объяснить различие между рассчитанными теоретически и полученными экспериментально значениями g. 7. Объясните, почему теплоемкость газа при постоянном давлении больше теплоемкости газа при постоянном объеме.
СПИСОК ЛИТЕРАТУРЫ
1. Савельев И.В. Курс общей физики, т. 1. М.: Наука, 1987, - 423 с. 2. Расчет погрешностей в лабораторных работах физического практикума. Методические указания к вводным занятиям в физическом практикуме / Н.А.Гринчар, Ф.П.Денисов, Б.А.Курбатов, В.А.Никитенко, А.П.Прунцев; Под общ. ред. Ф.П.Денисова. - М.: МИИТ, 1995. - с. 32.
РАБОТА №12 Введение
Известно, что звуковая волна в воздухе – продольная, и представляет собой совокупность распространяющихся в пространстве чередующихся областей разряжения и сжатия воздуха. Именно на эти разряжения и сжатия реагирует, в частности, барабанная перепонка уха человека.
Таким образом, скорость волны равна u= dL/dt. Однако, сами частицы во всем слое длиной dl будут двигаться со скоростью u = dl/dt, что соответствует скорости движения самого поршня. Поскольку поршень движется равномерно, то u = const. Массу dm частиц газа, которым передан импульс поршнем, можно представить в следующем виде: dm =r× S× dl = rSu× dt (где r - плотность газа). Это означает, что
Согласно второму закону Ньютона сила, действующая на газ со стороны поршня, равна скорости изменения его импульса: F = dp/dt, причём
Поскольку u = const, то F = u где F - сила давления поршня. Если учесть, что эта сила связана с избыточным давлением Dp, которое создаётся поршнем, соотношением F = Dp× S, то из (3) получим:
Dр = r× u× u. (4)
Отметим, что здесь рассматривается случай небольших сжатий, и отличиями площади S поперечного сечения трубы и плотности r воздуха в «несжатой» и в «сжатой» областях можно пренебречь. В случае объемной деформации газа формула закона Гука записывается следующим образом [3]: Dр = - K× Здесь р - давление - аналог напряжения, K - модуль объемной упругости среды - аналог модуля Юнга, DV/V - относительная объемная деформация - аналог относительного сжатия. Объем газа, деформируемый за время Dt, легко подсчитать как:
V = u× S× Dt. (6)
Саму деформацию объема можно представить в виде
DV= - S× u× Dt.(7)
Знак «-» показывает, что при увеличении скорости поршня среда сжимается, а при уменьшении - расширяется. Учитывая выражения (6) и (7), можно переписать формулу закона Гука: Dр = K× Теперь, используя выражение (4), из уравнения (8) получим, что скорость uзвука звуковой волны: uзвука = Воспользовавшись формулой (5), приходим к выражению: K = - V
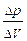 = - V× = - V×  . (10) . (10)
Поскольку V× r = m = const, то К = r uзвука =
Ньютон предположил, что закон изменения давления и плотности газа в звуковой волне соответствует закону Бойля-Мариотта: выполняется условие uзвука =
Это и есть формула Ньютона. Формулу Ньютона можно преобразовать, используя закон Клапейрона– Менделеева (выразив давление р газа через его плотность r):
р = где R = 8, 31 Дж/(моль× К) – универсальная газовая постоянная, m – молярная масса газа, Т – его температура. В результате получаем:
uзвука =
Пользуясь этой формулой, можно вычислить, чему равна молярная масса воздуха m (если знать, чему равны uзвука, T и R). Однако, как показали дальнейшие исследования, различные области газа, по которому распространяется звуковая волна, имеют неодинаковую температуру (на это впервые указал П. Лаплас в 1816 году). Применим его подход к рассмотрению структуры звуковой волны. Звуковая волна представляет собой чередующиеся в пространстве области разрежения и сжатия воздуха. Для сжатия воздуха внешние силы должны совершить работу над газом, в результате чего его температура в этой области будет несколько выше, чем в соседних. В разреженных же областях газ наоборот совершает работу и при этом охлаждается. Процесс сжатия-разрежения идет достаточно быстро, и температура не успевает выравниваться. Теплообменом можно пренебречь, поскольку теплопроводность воздуха в обычных условиях достаточно мала. Сказанное означает, что процесс сжатия-разрежения надо считать адиабатическим, а не изотермическим. Дифференцируя уравнение Пуассона для адиабатического процесса р× Vg= сonst, в котором g = Сp /СV (отношение молярных теплоемкостей газа при постоянных давлении и объеме), можно записать:
dр× V g+g× р× V g-1× dV =0, или dр× V +g× р× dV =0. (14)
Если учесть, что r × V = const, то можно перейти к уравнению вида:
g× р× dr =r× dр, то есть
Тогда, используя уравнение (15) и закон Клапейрона – Менделеева, формула для скорости звуковой волны в газе будет выглядеть так:
uзвука =
Измерив температуру Т воздуха, и приняв во внимание, что его можно с хорошей точностью считать двухатомным идеальным газом, (в этом случае показатель степени в уравнении Пуассона легко рассчитывается теоретически: g = 1, 4), для определения m по формуле (16) остаётся найти только скорость uзвука звуковой волны.
Порядок выполнения работы
Подать на " X" пластины осциллографа такое же напряжение со звукового генератора, каким возбуждается звуковая волна. Подать на " Y" пластины осциллографа напряжение с микрофона. Частоту генератора выбрать в пределах от 1 до 2 кГц. Занести выбранное значение в таблицу 1. 2. Настроить осциллограф (см. указания на стенде) и наблюдать на экране стабильный эллипс. Замерить расстояние от источника до приемника х1 и занести его значение в таблицу. 3. Смещая приемник, наблюдать поворот эллипса на 360°. Замерить при этом расстояние от источника до приемника (х2= х1+ Dх). 4. Повторить измерения по пп. 2, 3 не менее четырёх раз. 5. Выполнить измерения по пп. 2, 3, 4 на другой частоте и результаты занести в таблицу 2. 6. Измерить температуру воздуха с помощью термометра.
МЕТАЛЛОВ МЕТОДОМ ОХЛАЖДЕНИЯ
Цель работы. Ознакомление с относительным методом определения теплоемкости металлов. Вычисление теплоемкости неизвестного металла путем анализа кривых временного спада температуры для эталонного и исследуемого образцов. Приборы и принадлежности. Исследуемый образец, термопара, милливольтметр, секундомер, нагревательная печь, миллиметровая бумага и калька (заготавливается студентом).
Введение
Одной из важнейших задач физического эксперимента является определение параметров, характеризующих физические свойства объектов исследований. К необходимым параметрам по праву можно отнести теплоемкость. Теплоемкостью какого-либо тела называется величина равная количеству теплоты, которую нужно сообщить телу, чтобы повысить его температуру на один градус. Если сообщение телу количества теплоты dQ повышает его температуру на dT, то теплоемкость по определению равна: Стела = Эта величина измеряется в джоулях на кельвин (Дж/К) [1]. Теплоемкость весьма сложным образом может зависеть, в общем случае, от способа изменения температуры тела. Для газов, например, существенно, ведется ли нагревание (охлаждение) при постоянном объеме или при постоянном давлении [1]. Зависимость ее от температуры также сложна. Выбор конкретной физической модели, объясняющей ход зависимости С(T) может быть связан, кроме того, с родом материала (газ, твердое тело, жидкость), диапазоном температур и т.д. [2]. В частности, для металлов с простыми кристаллическими решетками и в определенном диапазоне температур (не слишком низких и не слишком высоких) достаточно хорошо «работает» теория Дебая. Однако к телам более сложной структуры формула Дебая не применима [3]. Очевидно, что получение значений теплоемкости при произвольной температуре для неизвестного материала является сложной и в то же время очень важной научно-технической задачей. В данной лабораторной работе используется оригинальный метод ее определения, предложенный сотрудниками НИИФ МГУ Я. А.Туровским и Г.М. Бартеневым в начале 40-х годов. Он был разработан для решения специальных задач, связанных с определением температурной зависимости теплоемкости металлов при высоких температурах [4][1]. Известно, что тело, нагретое до температуры выше температуры окружающей среды, со временем остывает, то есть, - отдает некоторое количество теплоты. Количество этого тепла, отданного за единицу времени, может быть выражено соотношением
где S - площадь поверхности тела, Tпов - температура поверхности тела; To - температура окружающей среды, a - коэффициент теплоотдачи[2]. Это же количество тепла может быть выражено через теплоемкость твердого тела:
где c - удельная теплоемкость материала (удельной теплоемкостью называется количество теплоты, которое необходимо сообщить единице массы тела, чтобы повысить ее температуру на один градус), r - плотность вещества, V - объем тела. Согласно закону сохранения энергии мы можем приравнять правые части выражений (1) и (2), т.е.:
Для дальнейших выкладок сделаем допущение, что теплоемкость и плотность вещества не зависят от объема, а коэффициент теплоотдачи постоянен по поверхности. Умножим и разделим левую часть равенства (3) на величину объема, а правую часть на величину поверхности. Тогда:
Величина
среднее значение разности Vcr При этом мы пренебрегаем малым изменением объема тела по сравнению с общим объемом тела в процессе охлаждения. Для эксперимента берутся два образца, изготовленные из различных материалов. В таком случае имеем следующую систему уравнений[3]:
VХ cХ rХ При изготовлении с достаточной степенью точности обеспечена идентичность объемов, формы образцов и площади поверхности. То есть можно считать, что VЭ » VХ, а SЭ » SХ. Учитывая эту особенность, легко можно получить соотношение для искомой теплоемкости: cХ = cЭ
cХ = cЭ Величины rХ, rЭ указаны на установке, cЭ - выбирается на основании данных таблицы (Приложение № 2). Относительно последнего допущения (aХ = aЭ) надо отметить, что оно может и не выполняться, поскольку коэффициент теплоотдачи является сложной функцией геометрических характеристик тела, температуры, скорости течения окружающего воздушного потока, плотности вещества и т.д. [7]. В данном опыте полностью устранить все указанные расхождения не удается. Равенства коэффициентов теплоотдачи можно пытаться достичь путём специальной обработки обеих поверхностей (например, - хромируя их [4] непосредственно перед измерениями). Но такое покрытие также теряет свои свойства со временем, поэтому в условиях учебной лаборатории выполняемые расчеты носят оценочный характер.
Описание установки
Корпус печки закреплён на направляющих рельсах 8. На этих рельсах установлен подвижный рейтер 9, на котором закреплен фарфоровый стержень с образцом. Рейтер фиксируется на рельсах винтом 10.
Порядок выполнения работы
Предварительные замечания. Так как на начальном этапе измерений температура образца спадает довольно быстро, то до включения установки следует заранее определить цену деления милливольтметра, заготовить таблицу 1, имеющую графы для занесения не менее 30 показаний; опробовать работу секундомера. Снятие показаний целесообразно, по тем же причинам, делать вдвоем. Например, один студент диктует отсчет показаний термо-эдс в делениях шкалы милливольтметра, а второй делает отсчет времени и записывает оба показания в таблицу. Внимание. Запрещается брать нагретый образец в руки и помещать любые предметы в отверстие печи.
1. Измерения. Для проведения измерений необходимо фарфоровый стержень с образцом 3 ввести в канал печки 2. С этой целью следует раскрепить винт 10, фиксирующий рейтер на рельсах и, перемещая его вдоль рельс, направить стержень с образцом в канал печки. После перемещения рейтера по рельсам 8 до упора 11 завернуть винт, фиксирующий рейтер 10. Контактные провода, идущие от термопары 5 необходимо подключить к милливольтметру 6. После этого включить в сеть кабель питания печки 7. Спустя некоторое время можно будет отметить рост показаний милливольтметра. Примерно через 15 - 20 минут они достигнут 9 - 10 мВ (порядка 200°С). В этот момент следует: - отключить кабель питания печки; - раскрепить винт 10 и вывести образец из зоны нагрева. Внимание: указанная процедура должна быть проделана быстро.
В ходе эксперимента фиксируются показания секундомера и соответствующие им значения напряжения, снимаемого с термопары; результаты заносятся в таблицу 1. Каждое очередное измерение проводится после уменьшения показаний милливольтметра на 0, 2 мВ (t1 - при 9, 0 мВ, t2 - при 8, 8 мВ, t3 - при 8, 6 мВ и т.д.). В интервале значений от 4 до 2 мВ показания можно снимать реже. Таблица 1 Популярное:
|
Последнее изменение этой страницы: 2016-08-31; Просмотров: 1101; Нарушение авторского права страницы