Связь момента импульса твёрдоготела с угловой скоростью еговращения. Тензор инерции. Главные и центральные оси инерции. Оси свободного вращения.

Момент импульса. Тензор инерции. Момент импульса тела относительно неподвижной точки – важнейшее понятие в динамике вращательного движения твердого тела. Он определяется так же, как и для системы материальных точек:

Здесь Dp_i=m_iv_i – импульс элементарной массы dm_i в лабораторной системе XYZ, а r_i – радиус-вектор массы dm_i с началом в той неподвижной точке, относительно которой вычисляется момент импульса тела. С учетом постоянства расстояний между точками абсолютно твердого тела вектор момента импульса L удается связать с вектором угловой скорости w.Рассмотрим, к примеру, две одинаковые точечные массы m, укрепленные на концах невесомого стержня АВ (рис. 2.3). Стержень с массами вращается с угловой скоростью w вокруг вертикальной оси, проходящей через середину стержня и перпендикулярной ему. В этом случае:

L=mr_i´ v_i+ mr₂´ v₂=2mr²w, здесь учтено, что: r₁ =r₂ =r, а v₁=v₁=wr.

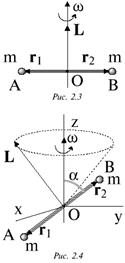Существенно, что в этом примере век тор L направлен так же, как и w. К сожалению, так бывает не всегда. В этом можно убедиться на примере, показанном на рис. 2.4. Получим выражение для L в случае твердого тела произвольной формы, закрепленного в некоторой точке О. Пусть r_i – радиус-вектор элементарной массы Dm_i твердого тела, а w –угловая скорость. Тогда:

Векторы r_i, w и L можно проектировать как на оси лабораторной системы XYZ, так и на оси системы xyz, жестко связанной с твердым телом (поскольку точка О неподвижна, начала обеих систем можно совместить). Преимущество системы xyz заключается в том, что в ней проекции r i являются постоянными величинами (в системе XYZ они зависят от времени), и выражения для компонент L оказываются проще.

ываются центробежными моментами инерции. Если J_xy=J_yx, J_xz=J_zx, J_zy=J_yz, то тензор наз. симметричным.

Если оси Ox, Oy, Oz совместить с главными осями инерции, то тензор инарциипримет дигональный вид. Величины J_xx=J_x, J_yy=J_y, J_xx=J_z в этом случае наз. главными моментами инрции тела, причём: L_x=J_xw_x и т. д. Эти оси также называются главными осями тензора инерции. Они жестко связаны с телом.

Направление главных осей тела часто можно определить, пользуюсь соображениями симметрии. Так, например, главные оси однородного прямоугольного параллелепипеда параллельны его рёбрам. К телам такого рода относится, например цилиндр.

Оси свободного вращения. Вращательное движение – это такое, при котором две точки тела остаются всё время неподвижными. Прямая, проходящая через эти точки, называется осью вращения. Все точки твердого тела, лежащие на оси вращения, неподвижны. Другие точки твердого тела движутся по окружностям в плоскостях, перпендикулярных оси вращения. Центры этих окружностей лежат на оси вращения. Вращательное двизение твердого тела является плоским.

Вопрос 2.

Колебания системы с двумя степенями свободы. Нормальные колебания(моды). нормальные частоты. Примеры.

Если система обладает несколикими слепенями свободы, то при малых отклонениях от положения равновесия возможны колебания сразу по всем степеням свободы. Обычный маятник может колебаться в двух взаимо перпендкудярных вертикальных плоскостях, проходящих через точку подвеса. Поэтому он имеет две степени свободы. Наличие связи раздичных степеней свободы между собой придает колебанию системы со многими степенями свободы новые физические закономерности.

Связанной системой называется система со многими степенями свободы, между которыми имеется связи, обеспечивающие возможность обмена энергией между различными степенями свободы. Примером связанной системы с двумя степенями свободы могут служить два маятника, соединенных между собой пружиной.

Несмотря на сложность движения двух связанных маятников, оно всегда может быть представлено как суперпоизция четырех гармонических колебаний, частоты которых называются нормальными частотами связанной системы. Число нормальных частот равно числу степеней свободы. В приведенном примере имеем две степени свободы. И можно представить колебание как суперпозицию двух колебаний.

ω I S^I₁(t)=S20sin(ω _I*t+φ _I)

S^I₂(t)=S₁₀sin(ω _I*t+φ _I)

ω I, S^I20/S^I10=1 – первая мода

ω I=√ (k/m)

ω II S^II₁(t)=S^II20*sin(ω _II*t+φ _II)

S^II₂(t)=S^II_10*sin(ω _II*t+φ _II)

ω II, S^II20 / S^II₁₀= -1 – вторая мода

ω II=√ ((k+2k1)/m)

S₁(t)=S^I10*sin(ω _I*t+φ _I)+S^II10*sin(ω _II*t+φ _II)

S₂(t)=S^I20*sin(ω _I*t+φ _I)+S^II20*sin(ω _II*t+φ _II)

ω I, ω II, S^I20/S^I10, S^II20 / S^II₁₀}à известны

Начальные условия S1(0), S1^'(0)

S₂(0), S₂^'(0) } → S^I10; φ _I

S^II10; φ _II

Еслимаятинки отклонить одинаково в одну сторону, то они колеблются с некоторой частотой ω 1, которая называется нормальной. Частота колебаний маятников, отклоненных одинаково в противоположных направлениях, является другой нормальной частотой ω 2.

Если ω _I≈ ω _II, |ω _I– ω _II| < < ω _I≈ ω _II,тогда отчетливо будут наблюдаться биения. Биение – колебание, которое происходит с медленой частотой и является суммой двух гармонических колебаний с близкими частотами. Это колебание с изменяющейся амплитудой. Оно лишь приблизительно гармоническое с частотой ω _I≈ ω _II, а его амплитуда изменяется с частотой |ω _I– ω _II|. T_биен=2p/(ω _I– ω _{II ).}

_Δω =ω _I– ω _II

< ω > =(ω _I+ω _II)/2

S₁(t)=2*S₁(t)*(cos( _Δω /2)t) *cos(< ω > t)

S₂(t)=2*S₁(t)*(sin(_Δω /2)t) *cos(< ω > t)

Билет 20.

Вопрос 1.

Закон сохранения момента импульса системы тел и его связь с изотропностью пространства. Примеры.

Момент импульса материальной точки. Пусть положение некоторойматериальной тоски относительно точки О, принятой за начало координат, характеризуется радиусом-вектором r. Моментом импусльса материальной точки относительно О называется вектор

L=r´ p.

Моментом импульса системы материальных точек относительно тоски О, принятой за начало, называется сумма моментов импульса, материальных точек, составляющих систему.

Закон сохранения момента импульса. Этот закон справедлив лишь для изолированных систем. Для них момент внешних сил М равен нулю и уравнение моментов принимает вид

dL/dt=0

Интегрируя это уравнение получаем

L=const,

L_x=const, L_y=const, L_z=const

Это равенство выразает закон сохранения момента импульса:

момент импусльса изолированной системы не изменяется при любых процессах, происходящих внутри системы.

Может случится, что система не является полностью изолированной, но на некоторое направление, например на ось z, проекция момента сил равна нулю. Тогда уравнение моментов озапишится в проециях в следующем виде:

dL_x/dt=M, dL_y/dt=M, dL_z/dt=0. L_z=const.

Поэтому закон сохранения момента импульса можно применять не только к полностью изолированным системам, но и к частичнро изолированным.

Связь закона сохранения момента импульса с изотропностью пространства. Под изотропностью пространстав понимается эквивалентность различных направлений в пространстве. Это означает, что если имеется некоторая изолированная физическая система, то развитие событий в ней зависитот того, как она ориентирована в пространстве. В применениии к изилированной системе материальных точек отсюда следует, что угловое перемещение системы на δ φ не изменит её внутреннего состояния и его внутренних движений. Поэтому полная работа внутренних сил при угловом перемещении должна быть равна нулю. При угловом перемещении δ φ материальная точка, характеризуемая радиусом вектором r_i , испытывает смещение δ r_i =δ φ *r_i. Равенство нулю полной работы внутренних сил при угловом перемещении системы на δ φ выражается в виде

½ *∑ ∑ (δ r_i∙ F_ji+δ r_i∙ F_ij)=0. (1)

Следовательно можно написать:

δ r_i∙ F_ji+δ r_i∙ F_ij=(δ φ ´ r_i)∙ F_ji+( δ φ ´ r_i)∙ F_ij=δ φ ∙ (r_i´ F_ji)+δ φ ´ (r_i´ F_ij)=δ φ ∙ [(r_i-r_j)´ F_ji], (2)

гдево внимание известное из векторной алгебры правило о циклической перестановке сомножетелей в смешанном векторном произведении и третий закон Ньютона. Пожставляя (2) в (1), находим ½ *∑ _i∑ _jδ φ ∙ [(r_i-r_j)*F_ji]=0. Поскольку угловое перемещение δ φ произвольно , получаем равенство ∑ _i∑ _j(r_i-r_j)*F_ji=0. Можно сказать, что полученное равенство следует из изотропности пространства. А это означает, что закон сохранения момента импульса изолированной системы материальных точек обусловлен фундаментальным свойством пространства в инерциальных система – его изотропностью.

Вопрос 2.

1 2 34