КИНЕМАТИКА МАТЕРИАЛЬНОЙ ТОЧКИ И ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА.
МЕХАНИКА.
КИНЕМАТИКА МАТЕРИАЛЬНОЙ ТОЧКИ И ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА.
1. Скорость 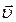 точки.
точки.
Перемещением материальной точки за время  называется вектор
называется вектор 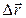 , соединяющий начальное и конечное положение этой точки. Путь
, соединяющий начальное и конечное положение этой точки. Путь 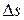 - расстояние, пройденное точкой по траектории за время
- расстояние, пройденное точкой по траектории за время  (рис.1).
(рис.1).
Рис.1.
Средней скоростью движения за время  называется величина
называется величина
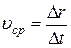 . (1)
. (1)
Скорость точки (ее также называют мгновенной скоростью)
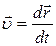 , (2)
, (2)
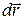 - перемещение за малое время
- перемещение за малое время 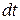 . Вектор
. Вектор 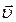 направлен по касательной к траектории движения, т.к. при
направлен по касательной к траектории движения, т.к. при 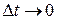 вектор
вектор 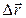 , секущий траекторию, становится касательным к ней вектором
, секущий траекторию, становится касательным к ней вектором 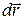 .
.
Т.к. модуль перемещения 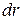 и расстояние
и расстояние 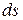 , пройденное за малое время, совпадают, то модуль вектора скорости равен производной от пути
, пройденное за малое время, совпадают, то модуль вектора скорости равен производной от пути 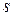 по времени
по времени 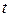
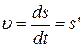 . (3)
. (3)
Соответственно путь 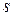 , пройденный за время
, пройденный за время 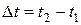 , равен интегралу от скорости
, равен интегралу от скорости  по времени
по времени 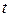
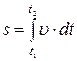 . (4)
. (4)
Движение материальной точки также описывают с помощью ее координат 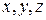 . В этом случае, чтобы определить скорость
. В этом случае, чтобы определить скорость  , сначала вычисляют проекции скорости на оси x, y, z, которые равны производным от соответствующих координат по времени
, сначала вычисляют проекции скорости на оси x, y, z, которые равны производным от соответствующих координат по времени
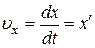 ,
, 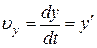 ,
, 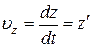 . (5)
. (5)
Тогда величина скорости
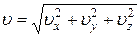 . (6)
. (6)
2. Ускорение 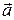 точки.
точки.
Ускорение характеризует быстроту изменения скорости
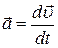 , (7)
, (7)
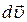 - изменение вектора скорости за малый промежуток времени
- изменение вектора скорости за малый промежуток времени 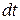 .
.
Ускорение 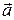 можно разложить на тангенциальное (его еще называют касательным) ускорение
можно разложить на тангенциальное (его еще называют касательным) ускорение 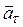 и нормальное (центростремительное) ускорение
и нормальное (центростремительное) ускорение 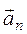 ,
,
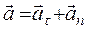 . (8)
. (8)
Тангенциальное ускорение 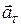 возникает, если скорость меняет величину, оно равно производной от скорости
возникает, если скорость меняет величину, оно равно производной от скорости 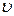 по времени
по времени 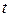 ,
,
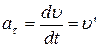 . (9)
. (9)
При движении с постоянной по величине скоростью 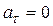 .
.
Нормальное ускорение
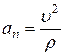 , (10)
, (10)
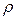 - радиус кривизны траектории в данной ее точке. Радиус кривизны
- радиус кривизны траектории в данной ее точке. Радиус кривизны 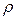 равен радиусу окружности, дуга которой совпадает с участком траектории.
равен радиусу окружности, дуга которой совпадает с участком траектории.
Для траектории, представляющей собой прямую линию, 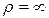 и
и 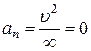 . Т.е. нормальное ускорение возникает только при искривлении траектории движения, когда вектор скорости
. Т.е. нормальное ускорение возникает только при искривлении траектории движения, когда вектор скорости 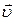 меняет свое направление.
меняет свое направление.
Если траектория точки – окружность, то радиус кривизны равен радиусу окружности, 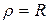 , и
, и 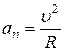 .
.
Тангенциальное ускорение 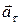 направлено по касательной к траектории; направление
направлено по касательной к траектории; направление 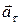 совпадает с направлением вектора скорости
совпадает с направлением вектора скорости 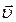 при ускоренном движении и противоположно ему при замедленном. Нормальное ускорение
при ускоренном движении и противоположно ему при замедленном. Нормальное ускорение 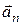 перпендикулярно
перпендикулярно 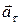 и направлено в сторону вогнутости траектории (рис.2). Т.к. векторы
и направлено в сторону вогнутости траектории (рис.2). Т.к. векторы 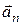 и
и 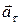 перпендикулярны, то величина полного ускорения
перпендикулярны, то величина полного ускорения
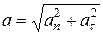 . (11)
. (11)
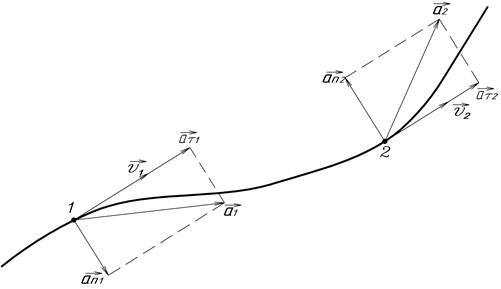
Рис.2.
При координатном способе задания движения, чтобы определить ускорение, сначала вычисляют его проекции на оси x, y, z
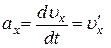 ,
, 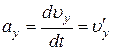 ,
, 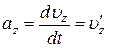 . (12)
. (12)
Величина ускорения в этом случае
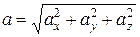 . (13)
. (13)
Формулы прямолинейного равноускоренного движения.
Если тело (материальная точка) движется вдоль оси х с постоянным ускорением, проекция которого на эту ось равна 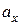 , то зависимость координаты тела
, то зависимость координаты тела 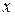 от времени
от времени 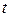 описывается уравнением
описывается уравнением
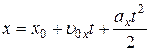 . (14)
. (14)
Проекция 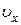 скорости в момент
скорости в момент 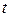 равна
равна
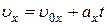 . (15)
. (15)
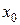 - начальная координата и
- начальная координата и 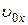 - проекция скорости на ось х в момент времени
- проекция скорости на ось х в момент времени 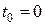 .
.
Формулы равноускоренного движения используются при решении задач на падение тел вблизи поверхности Земли, т.к. такое движение происходит под действием силы тяжести с постоянным ускорением 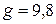 м/c2 (ускорение свободного падения тел).
м/c2 (ускорение свободного падения тел).
Поступательное движение тела.
Поступательным называется движение, при котором любая прямая, проведенная в теле, перемещается параллельно самой себе. Т.к. при поступательном движении траектории, скорости и ускорения всех точек тела совпадают, то для описания движения тела достаточно рассмотреть движение любой его точки.
Формулы равноускоренного вращения.
Если угловое ускорение  постоянно, то
постоянно, то
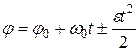 (24)
(24)
и
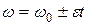 , (25)
, (25)
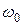 и
и 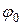 – угловая скорость и угол поворота тела в начальный момент
– угловая скорость и угол поворота тела в начальный момент 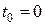 ,
,
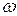 и
и 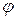 – в момент времени
– в момент времени 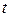 . При ускоренном вращении в уравнениях (24) - (25) выбирается знак «+», а при замедленном – знак «-».
. При ускоренном вращении в уравнениях (24) - (25) выбирается знак «+», а при замедленном – знак «-».
ДИНАМИКА.
ЗАКОНЫ НЬЮТОНА.
Законы Ньютона.
В основе классической механики лежат законы Ньютона.
1-й закон: если сумма сил, действующих на тело, равна нулю ( 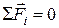 ), то тело или покоится, или движется прямолинейно и равномерно.
), то тело или покоится, или движется прямолинейно и равномерно.
2-й закон: произведение массы 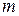 тела на его ускорение
тела на его ускорение 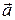 равно сумме сил, действующих на тело,
равно сумме сил, действующих на тело,
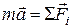 . (26)
. (26)
3-й закон: с какой силой первое тело действует на второе, с такой же по величине и обратной по направлению силой второе тело действует на первое.
Системы отсчета, в которых справедливы законы Ньютона, называются инерциальными.
СИЛЫ В МЕХАНИКЕ.
Гравитационная сила.
Две точечные массы  и
и 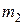 , расположенные на расстоянии
, расположенные на расстоянии 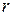 друг от друга, притягиваются с силой
друг от друга, притягиваются с силой
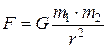 , (27)
, (27)
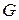 =6, 67·10-11 м3/(кг·с2) – гравитационная постоянная. Уравнение (27) представляет собой закон всемирного тяготения.
=6, 67·10-11 м3/(кг·с2) – гравитационная постоянная. Уравнение (27) представляет собой закон всемирного тяготения.
2. Сила тяжести.
Силой тяжести тела массой 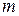 называется сила притяжения его к Земле
называется сила притяжения его к Земле
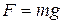 , (28)
, (28)
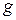 – ускорение свободного падения.
– ускорение свободного падения.
Вследствие суточного вращения Земли и несферичности ее формы величина 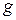 различается от 9, 78 м/с2 на экваторе до 9, 83 м/с2 на полюсах. В среднем на поверхности Земли
различается от 9, 78 м/с2 на экваторе до 9, 83 м/с2 на полюсах. В среднем на поверхности Земли
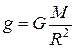 =9, 8 м/с2,
=9, 8 м/с2,
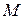 и
и 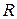 - масса и радиус Земли.
- масса и радиус Земли.
На высоте  над поверхностью Земли
над поверхностью Земли
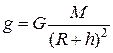 . (29)
. (29)
Вес тела.
Вес представляет собой силу, с которой тело действует на горизонтальную опору или на подвес.
По величине вес и сила тяжести совпадают только в том случае, если опора неподвижна. Например, вес тела, находящегося в движущемся вверх с ускорением лифте, превышает его силу тяжести.
Сила трения.
При скольжении тела действующая на него сила трения
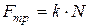 , (30)
, (30)
 - коэффициент трения,
- коэффициент трения, 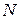 - сила реакции опоры (рис. 4 ).
- сила реакции опоры (рис. 4 ).
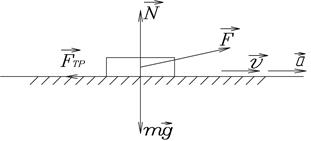
Рис.4.
Сила упругости.
Сила упругости, действующая на тело со стороны деформированной (сжатой или растянутой) пружины, равна по величине
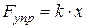 , (31)
, (31)
 - коэффициент упругости (жесткость) пружины,
- коэффициент упругости (жесткость) пружины, 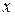 - величина деформации пружины.
- величина деформации пружины.
Момент инерции тела.
Моментом инерции 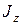 тела относительно какой-либо оси z называется сумма произведений масс точек этого тела на квадраты расстояний от этих точек до оси
тела относительно какой-либо оси z называется сумма произведений масс точек этого тела на квадраты расстояний от этих точек до оси
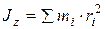 , (42)
, (42)
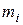 - масса
- масса 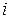 -той точки,
-той точки, 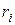 - кратчайшее расстояние от
- кратчайшее расстояние от 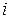 -той точки до оси z.
-той точки до оси z.
Для сплошных тел момент инерции определяется через интеграл
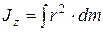 , (43)
, (43)
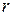 - расстояние от элемента
- расстояние от элемента 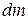 массы тела до оси z.
массы тела до оси z.
Моменты инерции однородных тел простой геометрической формы обычно рассчитывают по формуле (43), а сложной определяют экспериментально. В таблице 1 приведены моменты инерции некоторых тел.
Теорема Штейнера. Если для какого-либо тела известен его момент инерции 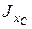 относительно оси
относительно оси 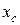 , проходящей через центр масс
, проходящей через центр масс  тела, то момент инерции этого тела относительно оси
тела, то момент инерции этого тела относительно оси 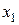 , параллельной
, параллельной 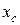 , равен
, равен
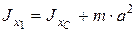 , (44)
, (44)
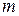 - масса тела,
- масса тела, 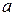 - кратчайшее расстояние между осями
- кратчайшее расстояние между осями 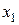 и
и 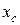 .
.
Условия равновесия тел.
Из 2-го закона Ньютона 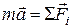 и основного уравнения динамики вращательного движения
и основного уравнения динамики вращательного движения 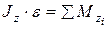 следуют условия равновесия тел: для покоящегося тела
следуют условия равновесия тел: для покоящегося тела
1) сумма действующих на тело сил должна быть равной нулю,
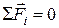 ,
,
или, если использовать проекции сил, то
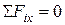 и
и 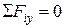 ; (46)
; (46)
2) сумма моментов сил относительно любой точки тела должна быть равна нулю
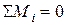 . (47)
. (47)
Таблица 1. Моменты инерции некоторых тел.
4. Момент импульса 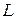 .
.
Моментом 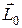 импульсаматериальной точки массой
импульсаматериальной точки массой 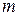 , движущейся со скоростью
, движущейся со скоростью 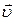 , относительно какой-либо точки отсчета
, относительно какой-либо точки отсчета 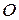 , называют векторное произведение
, называют векторное произведение
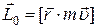 ,
,
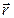 - радиус-вектор материальной точки (рис.7),
- радиус-вектор материальной точки (рис.7), 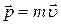 - ее импульс.
- ее импульс.
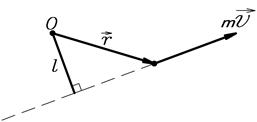
Рис.7.
Величина момента импульса материальной точки
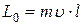 , (48)
, (48)
где 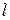 -кратчайшее расстояние от линии вектора
-кратчайшее расстояние от линии вектора 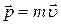 до точки
до точки 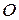 .
.
Для вращающегося тела момент импульса 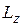 относительно оси вращения
относительно оси вращения 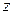
равен
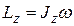 , (49)
, (49)
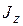 - момент инерции тела относительно оси
- момент инерции тела относительно оси 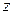 и
и 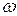 - его угловая скорость.
- его угловая скорость.
Скорость изменения момента импульса системы тел равна сумме моментов сил, приложенных к этой системе
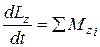 .
.
Тогда
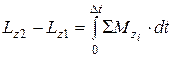 . (50)
. (50)
Если моменты сил постоянны, то уравнение (50) можно записать в виде
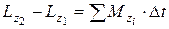 , (51)
, (51)
т.е. изменение момента импульса системы тел относительно какой-либо оси 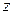 равно сумме моментов сил, действующих на эту систему, умноженной на время
равно сумме моментов сил, действующих на эту систему, умноженной на время 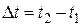 .
.
Отсюда следует закон сохранения момента импульса: момент импульса 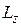 системы тел относительно оси
системы тел относительно оси 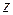 сохраняется, если сумма моментов сил
сохраняется, если сумма моментов сил 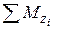 , действующих на эту систему, равна нулю.
, действующих на эту систему, равна нулю.
РАБОТА И ЭНЕРГИЯ.
Работа силы.
Работа 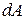 , выполняемая силой
, выполняемая силой 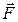 при малом перемещении
при малом перемещении 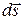 тела, определяется следующим образом
тела, определяется следующим образом
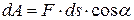 , (52)
, (52)
или
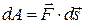 ,
,
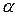 - угол между направлениями силы и перемещения. Если сила
- угол между направлениями силы и перемещения. Если сила 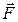 перпендикулярна перемещению
перпендикулярна перемещению 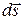 , т.е.
, т.е. 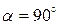 , то работа силой не совершается, т.к.
, то работа силой не совершается, т.к. 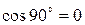 .
.
Полная работа на пути 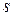
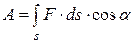 . (53)
. (53)
Если тело движется прямолинейно и действующая на тело сила 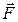 постоянна, то есть
постоянна, то есть  и
и 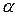 не меняются, то работа силы на пути
не меняются, то работа силы на пути 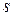 равна
равна
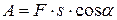 . (54)
. (54)
Единица измерения работы 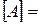 Дж (Джоуль).
Дж (Джоуль).
· Работу силы тяжести 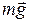 можно подсчитать по упрощенной формуле
можно подсчитать по упрощенной формуле
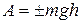 , (55)
, (55)
 - величина перемещения тела вдоль действия силы тяжести, «
- величина перемещения тела вдоль действия силы тяжести, « 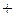 » выбирается при движении тела вниз, «-» - при движении тела вверх.
» выбирается при движении тела вниз, «-» - при движении тела вверх.
· Работа силы упругости 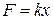 равна
равна
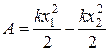 , (56)
, (56)
 - коэффициент упругости пружины,
- коэффициент упругости пружины, 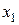 и
и 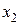 - ее начальная и конечная деформации.
- ее начальная и конечная деформации.
Силы, работа 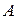 которых не зависит от траектории движения тела, а определяется его начальным и конечным положением, называются консервативными. В механике к таким силам относятся сила тяжести
которых не зависит от траектории движения тела, а определяется его начальным и конечным положением, называются консервативными. В механике к таким силам относятся сила тяжести 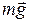 и сила упругости
и сила упругости 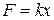 .
.
Мощность 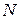 представляет собой работу, произведенную в единицу времени, т.е.
представляет собой работу, произведенную в единицу времени, т.е.
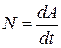 , (57)
, (57)
где 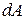 - работа, совершенная за время
- работа, совершенная за время 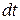 . Единицей измерения мощности является Ватт (Вт).
. Единицей измерения мощности является Ватт (Вт).
Работа момента силы.
При вращении, когда тело поворачивается на малый угол 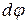 , момент
, момент 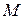 силы совершает работу
силы совершает работу
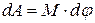 . (58)
. (58)
При повороте на угол 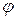 работа равна
работа равна
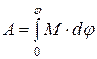 .
.
Если момент силы не зависит от угла поворота, то
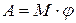 . (59)
. (59)
Механическая энергия.
Энергия является мерой способности тел совершать работу. Механическая энергия складывается из кинетической и потенциальной. Первая обусловлена движением тела, вторая - видом сил, действующих на тело и положением тела в пространстве.
Для материальной точки и поступательно движущегося тела кинетическая энергия равна
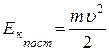 , (60)
, (60)
для вращающегося телаона представляет собой сумму кинетических энергий отдельных точек тела
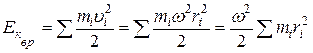 .
.
В итоге, для вращающегося тела,
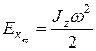 . (61)
. (61)
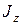 - момент инерции тела относительно оси вращения,
- момент инерции тела относительно оси вращения, 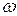 - его угловая скорость.
- его угловая скорость.
Потенциальной энергией обладают тела, находящиеся под действием консервативных сил. Если тело перемещается консервативными силами из точки 1 в точку 2, то изменение потенциальной энергии 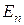 тела определяется как работа этих сил
тела определяется как работа этих сил
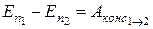 . (62)
. (62)
Из (62) можно найти только изменение потенциальной энергии, ее величина может быть определена лишь с точностью до постоянного слагаемого. Поэтому начало отсчета потенциальной энергии может быть выбрано произвольно.
Консервативная сила  по величине равна скорости изменения потенциальной энергии в направлении
по величине равна скорости изменения потенциальной энергии в направлении 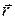 действия силы,
действия силы,
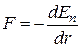 . (63)
. (63)
Знак минус в уравнении (63) отражает тот факт, что консервативная сила 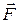 всегда направлена в сторону убыли потенциальной энергии.
всегда направлена в сторону убыли потенциальной энергии.
Если тело находится под действием силы тяжести, его потенциальная энергия

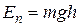 , (64)
, (64)
 - высота расположения тела над уровнем отсчета.
- высота расположения тела над уровнем отсчета.
Если на тело действует сила упругости, его потенциальная энергия
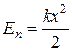 , (65)
, (65)
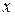 - величина деформации пружины.
- величина деформации пружины.
Давление
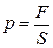 ,
, 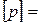 Па (Паскаль). (69)
Па (Паскаль). (69)
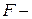 сила, действующая перпендикулярно площадке
сила, действующая перпендикулярно площадке 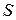 .
.
Законы гидростатики.
1. Закон Паскаля. Давление, оказываемое на жидкость, передается во все ее точки, по всем направлениям, без изменения.
2. Гидростатическое давление. Гидростатическим называется давление, обусловленное весом жидкости. Величина гидростатического давления
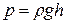 , (70)
, (70)
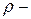 плотность жидкости,
плотность жидкости, 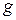 - ускорение свободного падения,
- ускорение свободного падения,  - высота столба жидкости. Уровни равного давления в жидкости всегда горизонтальны.
- высота столба жидкости. Уровни равного давления в жидкости всегда горизонтальны.
3. Закон Архимеда. На тело, погруженное в жидкость (газ), действует выталкивающая сила Архимеда
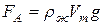 , (71)
, (71)
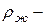 плотность жидкости,
плотность жидкости, 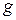 - ускорение свободного падения,
- ускорение свободного падения, 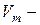 объем тела, погруженного в жидкость.
объем тела, погруженного в жидкость.
Законы гидродинамики.
Уравнение Бернулли.
Жидкость называется идеальной (невязкой), если можно пренебречь силами трения между ее слоями.
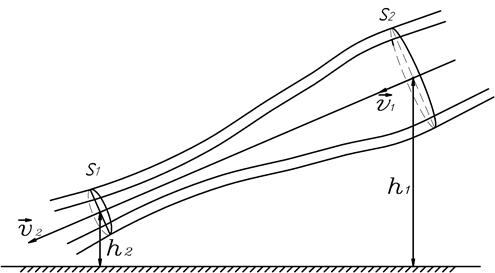
Рис.8.
Для идеальной жидкости при ламинарном течении выполняется уравнение Бернулли
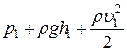 =
= 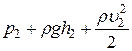 , (73)
, (73)
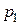 и
и  - статическое давление (давление жидкости на площадку, расположенную вдоль линии тока) в сечениях 1 и 2 трубки тока (рис. 8);
- статическое давление (давление жидкости на площадку, расположенную вдоль линии тока) в сечениях 1 и 2 трубки тока (рис. 8);
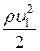 и
и 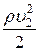 - динамическое давление в этих сечениях, обусловленное движением жидкости;
- динамическое давление в этих сечениях, обусловленное движением жидкости;
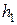 и
и 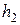 - высоты, на которых расположены сечения;
- высоты, на которых расположены сечения;
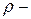 плотность жидкости.
плотность жидкости.
Замедление времени.
Пусть 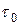 - длительность события в точке, неподвижной относительно системы отсчета x, y (время
- длительность события в точке, неподвижной относительно системы отсчета x, y (время 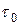 называют « собственным временем»). Обозначим через
называют « собственным временем»). Обозначим через 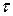 длительность этого же события в системе x’y’, относительно которой система x, y движется со скоростью
длительность этого же события в системе x’y’, относительно которой система x, y движется со скоростью  . Интервалы времени
. Интервалы времени 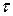 и
и 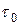 связаны соотношением
связаны соотношением
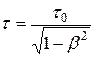 , (74)
, (74)
где 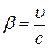 . Всегда параметр
. Всегда параметр 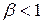 и
и 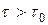 , т.е. длительность события, происходящего в определенной точке, является наименьшей в системе отсчета, относительно которой эта точка неподвижна.
, т.е. длительность события, происходящего в определенной точке, является наименьшей в системе отсчета, относительно которой эта точка неподвижна.
Сокращение длины.
Обозначим через 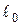 длину тела в системе отсчета, относительно которой тело покоится, а через
длину тела в системе отсчета, относительно которой тело покоится, а через 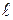 - длину в системе, относительно которой оно движется со скоростью
- длину в системе, относительно которой оно движется со скоростью  . Тогда
. Тогда
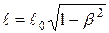 . (75)
. (75)
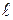 <
< 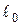 , т.е. длина тела наибольшая в системе отсчета, относительно которой тело неподвижно. Сокращение длины происходит только в направлении движения тела, поперечные движению размеры тела не зависят от скорости его движения и одинаковы во всех инерциальных системах отсчета.
, т.е. длина тела наибольшая в системе отсчета, относительно которой тело неподвижно. Сокращение длины происходит только в направлении движения тела, поперечные движению размеры тела не зависят от скорости его движения и одинаковы во всех инерциальных системах отсчета.
5. Зависимость массы 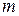 тела от скорости его движения.
тела от скорости его движения.
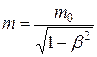 , (76)
, (76)
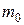 -масса покоя тела, т.е. масса в системе отсчета, относительно которой тело покоится.
-масса покоя тела, т.е. масса в системе отсчета, относительно которой тело покоится.
6. Импульс 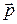 частицы.
частицы.
Импульс релятивистской частицы
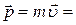
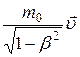 .
.
Основной закон релятивистской динамики материальной точки
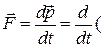
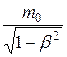
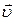 ),
),
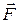 - результирующая всех сил, приложенных к этой точке.
- результирующая всех сил, приложенных к этой точке.
МЕХАНИКА.
КИНЕМАТИКА МАТЕРИАЛЬНОЙ ТОЧКИ И ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА.
1. Скорость 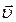 точки.
точки.
Перемещением материальной точки за время  называется вектор
называется вектор 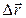 , соединяющий начальное и конечное положение этой точки. Путь
, соединяющий начальное и конечное положение этой точки. Путь 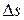 - расстояние, пройденное точкой по траектории за время
- расстояние, пройденное точкой по траектории за время  (рис.1).
(рис.1).
Рис.1.
Средней скоростью движения за время  называется величина
называется величина
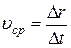 . (1)
. (1)
Скорость точки (ее также называют мгновенной скоростью)
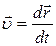 , (2)
, (2)
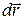 - перемещение за малое время
- перемещение за малое время 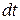 . Вектор
. Вектор 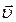 направлен по касательной к траектории движения, т.к. при
направлен по касательной к траектории движения, т.к. при 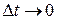 вектор
вектор 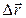 , секущий траекторию, становится касательным к ней вектором
, секущий траекторию, становится касательным к ней вектором 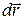 .
.
Т.к. модуль перемещения 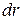 и расстояние
и расстояние 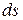 , пройденное за малое время, совпадают, то модуль вектора скорости равен производной от пути
, пройденное за малое время, совпадают, то модуль вектора скорости равен производной от пути 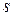 по времени
по времени 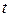
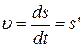 . (3)
. (3)
Соответственно путь 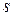 , пройденный за время
, пройденный за время 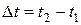 , равен интегралу от скорости
, равен интегралу от скорости  по времени
по времени 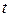
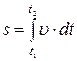 . (4)
. (4)
Движение материальной точки также описывают с помощью ее координат 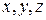 . В этом случае, чтобы определить скорость
. В этом случае, чтобы определить скорость  , сначала вычисляют проекции скорости на оси x, y, z, которые равны производным от соответствующих координат по времени
, сначала вычисляют проекции скорости на оси x, y, z, которые равны производным от соответствующих координат по времени
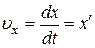 ,
, 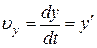 ,
, 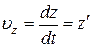 . (5)
. (5)
Тогда величина скорости
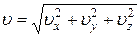 . (6)
. (6)
2. Ускорение 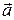 точки.
точки.
Ускорение характеризует быстроту изменения скорости
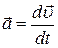 , (7)
, (7)
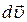 - изменение вектора скорости за малый промежуток времени
- изменение вектора скорости за малый промежуток времени 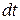 .
.
Ускорение 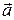 можно разложить на тангенциальное (его еще называют касательным) ускорение
можно разложить на тангенциальное (его еще называют касательным) ускорение 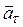 и нормальное (центростремительное) ускорение
и нормальное (центростремительное) ускорение 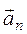 ,
,
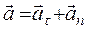 . (8)
. (8)
Тангенциальное ускорение 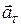 возникает, если скорость меняет величину, оно равно производной от скорости
возникает, если скорость меняет величину, оно равно производной от скорости 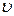 по времени
по времени 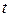 ,
,
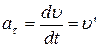 . (9)
. (9)
При движении с постоянной по величине скоростью 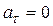 .
.
Нормальное ускорение
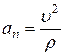 , (10)
, (10)
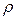 - радиус кривизны траектории в данной ее точке. Радиус кривизны
- радиус кривизны траектории в данной ее точке. Радиус кривизны 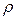 равен радиусу окружности, дуга которой совпадает с участком траектории.
равен радиусу окружности, дуга которой совпадает с участком траектории.
Для траектории, представляющей собой прямую линию, 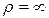 и
и 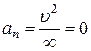 . Т.е. нормальное ускорение возникает только при искривлении траектории движения, когда вектор скорости
. Т.е. нормальное ускорение возникает только при искривлении траектории движения, когда вектор скорости 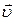 меняет свое направление.
меняет свое направление.
Если траектория точки – окружность, то радиус кривизны равен радиусу окружности, 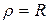 , и
, и 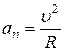 .
.
Тангенциальное ускорение 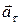 направлено по касательной к траектории; направление
направлено по касательной к траектории; направление 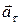 совпадает с направлением вектора скорости
совпадает с направлением вектора скорости 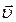 при ускоренном движении и противоположно ему при замедленном. Нормальное ускорение
при ускоренном движении и противоположно ему при замедленном. Нормальное ускорение 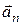 перпендикулярно
перпендикулярно 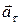 и направлено в сторону вогнутости траектории (рис.2). Т.к. векторы
и направлено в сторону вогнутости траектории (рис.2). Т.к. векторы 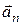 и
и 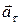 перпендикулярны, то величина полного ускорения
перпендикулярны, то величина полного ускорения
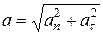 . (11)
. (11)

Рис.2.
При координатном способе задания движения, чтобы определить ускорение, сначала вычисляют его проекции на оси x, y, z
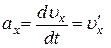 ,
, 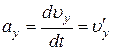 ,
, 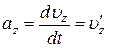 . (12)
. (12)
Величина ускорения в этом случае
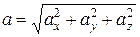 . (13)
. (13)
Популярное:

