РАЗРАБОТКА КИНЕМАТИЧЕСКОЙ СХЕМЫ

ПРИКЛАДНАЯ МЕХАНИКА

Задания и методические указания к выполнению

курсового проекта (спец. 190100); курсовой работы (спец.210200)

Факультет машиностроительный

Направления и специальности подготовки дипломированных специалистов:

653700 – приборостроение

190100 – приборостроение

657900 – автоматизированные технологии и производства

210200 – автоматизация технологических процессов и производств

Направления подготовки бакалавров:

551500 – приборостроение

552900 – технология, оборудование и автоматизация

Санкт-Петербург

Утверждено редакционно-издательским советом университета

УДК 621.01 (07)

Прикладная механика: Задание и методические указания к выполнению курсового проекта (спец. 190100), курсовой работы (спец.210200).

– СПб: СЗТУ, 2003 – 38 с.

Задания и методические указания разработаны на основании государственных образовательных стандартов высшего профессионального образования по направлениям подготовки дипломированных специалистов: 653700, 657900 (специальности: 190100, 210200) и направлениям подготовки бакалавров: 551500, 552900.

Курсовой проект (курсовая работа) предусматривает решение комплексной задачи по проектированию механизмов контрольно-измерительного автомата. В процессе выполнения работы студенты знакомятся с последовательностью расчетов, приобретают навыки кинематического и динамического анализа и синтеза механизмов, оформляют чертежи и пояснительную записку.

Рассмотрено на заседании кафедры теоретической и прикладной механики 26.12 2002; одобрено методической комиссией машиностроительного факультета от 23 июня 2003 года.

Рецензенты: кафедра теоретической и прикладной механики СЗТУ

(заведующий кафедрой В.В.Гурецкий, д-р техн. наук, проф.); А.В. Троицкий, д-р техн. наук, проф., нач. лаборатории ЦНИИ им. А.Н. Крылова.

Составители: К.У. Кутыев, канд. техн. наук, доц;

А.И. Иванов, канд. техн. наук, доц;

О.А. Румянцев, канд. техн. наук, доц.

ВВЕДЕНИЕ

Курсовой проект (курсовая работа) предусматривает решение комплексной задачи, охватывающей основные разделы дисциплины «Прикладная механика». В процессе выполнения задания студент должен познакомиться с последовательностью расчетов агрегатов, машин, механизмов и деталей общего назначения; приобрести навыки структурного, кинематического и динамического исследования агрегата в целом; выполнить инженерные расчеты механизмов контрольно-измерительного автомата; приобрести навыки оформления чертежей и пояснительной записки.

I. ЗАДАНИЕ НА КУРСОВОЙ ПРОЕКТ

(КУРСОВУЮ РАБОТУ)

По заданной кинематической схеме и исходным данным спроектировать механизмы поворота стола контрольно-измерительного автомата (КИА), рис.1…5.

Кинематическая схема включает планетарную зубчатую передачу, коническую зубчатую пару, мальтийский и кривошипно-ползунный механизмы.

Каждый студент выполняет курсовой проект (курсовую работу) по индивидуальному заданию, вариант которого определяется двумя последними цифрами шифра.

Производительность автомата, схема планетарной передачи, число сателлитов и некоторые параметры механизмов выбираются по предпоследней цифре шифра студента по табл.1.

Моменты сил сопротивления, моменты инерции, а также другие данные определяются последней цифрой шифра по табл.2.

В содержание курсовой работы студентов специальности 210200 не входят расчеты по разделам и подразделам: 6.1.3, 6.2.3, 8, 9, а также сокращается соответствующая им графическая часть.

Допускается выбор темы задания, имеющей практическое значение для организации, в которой работает студент. В этом случае студент должен предварительно согласовать содержание и получить разрешение руководителя на выполнение курсового проекта (курсовой работы) по выбранной теме.

В табл. 1 и 2 приняты следующие обозначения:

– производительность КИА (количество контролируемых деталей за один час);

– передаточное отношение конической зубчатой пары;

– число пазов мальтийского креста;

Рис.1 Рис.2

Рис.3 Рис.4

ИСХОДНЫЕ ДАННЫЕ Т а б л и ц а 1

Параметры Един. измерения ВАРИАНТЫ (предпоследняя цифра шифра)

СХЕМА ПЕРЕДАЧИ НА РИСУНКЕ

Дет./час

1, 75 1, 60 1, 50 1, 35 1, 25 1, 45 1, 55 1, 65 1, 70 1, 40

1/c

ИСХОДНЫЕ ДАННЫЕ Т а б л и ц а 2

Параметры Един. измерения ВАРИАНТЫ (последняя цифра шифра)

4, 5 4, 9 4, 4 5, 2 5, 0 4, 8 4, 7 4, 6 4, 2 5, 1

5, 2 5, 5 4, 9 5, 6 5, 6 5, 4 5, 6 5, 5 4, 8 5, 8

Н

2, 5 2, 8 3, 3, 2 3, 5 3, 4 3, 3 3, 1 2, 8 3, 3

1, 5 1, 4 1, 2 1, 0 0, 9 1, 2 1, 1 1, 3 1, 4 1, 2

2, 5 2, 4 2, 3 2, 6 2, 5 2, 7 2, 8 2, 6 2, 7 2, 8

1, 3 1, 4 1, 3 1, 5 1, 6 1, 7 1, 6 1, 3 1, 5 1, 3

м 0, 22 0, 24 0, 20 0, 25 0, 21 0, 23 0, 22 0, 24 0, 25 0, 23

0, 11 0, 14 0, 15 0, 12 0, 13 0, 12 0, 11 0, 14 0, 13 0, 15

0, 08 0, 05 0, 08 0, 05 0, 07 0, 06 0, 05 0, 06 0, 07 0, 07

0, 07 0, 05 0, 06 0, 05 0, 08 0, 07 0, 06 0, 05 0, 08 0, 07

0, 11 0, 10 0, 12 0, 13 0, 11 0, 14 0, 12 0, 13 0, 13 0, 12

0, 40 0, 35 0, 40 0, 32 0, 38 0, 40 0, 30 0, 31 0, 35 0, 34

0, 03 0, 02 0, 03 0, 02 0, 03 0, 02 0, 03 0, 02 0, 03 0, 02

– число сателлитов планетарной передачи;

– частота вращения ведущего вала 1;

– момент сил сопротивления транспортирующего устройства (рис.5);

– моменты сил трения в опорах валов 4 и 5 (рис.5);

– сила сопротивления при выталкивании деталей со стола;

– моменты инерций вращающихся масс относительно осей валов соответственно 3, 4, 5 (рис.5);

момент инерции относительно оси выходного вала планетарной передачи;

– межосевое расстояние мальтийского механизма (рис.6);

– размеры вала 4;

– диаметр делительной окружности конического колеса, установленного на валу 4;

– отношение длины r кривошипа к длине l шатуна кривошипно-ползунного механизма;

– коэффициент неравномерности вращения вала 4.

2. ОПИСАНИЕ РАБОТЫ КИА

Многопозиционные КИА предназначены для контроля и сортировки деталей в процессе обработки в условиях автоматизированного крупносерийного и массового производства. В таких автоматах для повышения их производительности контроль параметров деталей осуществляется на нескольких позициях одновременно. На первой позиции выполняется загрузка, а на последней – выталкивание деталей. На измерительных позициях контролируются последовательно различные параметры одной и той же детали.

На рис.5 изображена кинематическая схема четырехпозиционного автомата для измерения и контроля нескольких параметров деталей. Движение звеньев автомата осуществляется от ведущего вала 1 электродвигателя, связанного при помощи муфты с водилом Н планетарной передачи. От сателлита 2 с двумя зубчатыми венцами вращение передается на выходной вал передачи. Далее через соединительную муфту движение передается на вал 3, связанный цепной передачей с транспортирующим устройством (на рис.5 часть устройства показана пунктирными линиями). От вала 3 через коническую зубчатую пару вращение передается на вал 4 кривошипа мальтийского механизма. Для уменьшения неравномерности вращения на валу установлен маховик «М». Поворот вала 4 от входа цевки кривошипа в паз до выхода из паза называется углом рабочего поворота . При этом крест со столом поворачивается на угол .

Рис.5

Рис.6

ЦИКЛОГРАММА РАБОТЫ КИА Т а б л и ц а 3

СОСТОЯНИЕ ПОКОЯ

ХОЛОСТОЙ ПОВОРОТ

РАБОЧИЙ ПОВОРОТ

ПОВОРОТ

ПЕРЕМЕЩЕНИЕ НА ПОЗИЦИИ

ОБРАТНЫЙ ХОД

ПОЛЗУН

ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА

ДЕТАЛИ

МАЛЬТИЙСКИЙ КРЕСТ

КРИВОШИП С ЦЕВКОЙ

0

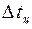
В момент выхода цевки из паза вращение креста и стола прекращается. Неподвижное положение креста и стола фиксируется цилиндрической поверхностью диска кривошипа, которая при повороте скользит по сегментному вырезу креста. На конце вала 4 имеется другой кривошип «К», который посредством шатуна 6 связан с ползуном 7. По истечении времени после остановки креста (см. табл. 3) при прямом ходе ползуна происходит выталкивание детали «Д» (см. рис.5). При неподвижном столе осуществляются следующие операции: контроль и измерение деталей на нескольких позициях, загрузка деталей на стол из бункера-накопителя и выталкивание при помощи ползуна 7 проконтролированной детали в лоток (бункер и лоток на рисунке не показаны). Продвижение деталей от предыдущих к последующим позициям осуществляется при повторяющихся циклических поворотах стола. Вокруг стола размещены измерительные станции (на рис.5 не показаны), которые работают с одинаковой длительностью контроля. Время цикла (см. табл.3) соответствует длительности одного оборота кривошипного вала 4. За каждый цикл в лоток сбрасывается одна проконтролированная деталь и подается из бункера на стол новая. При этом полный контроль (включая загрузку и выталкивание) одной детали на многопозиционном автомате выполняется за (здесь – число пазов креста).

ЗАДАЧИ ПРОЕКТИРОВАНИЯ КИА

По исходным данным необходимо:

1. Разработать кинематическую схему автомата.

2. Выполнить его структурный анализ.

3. Выполнить кинематический анализ КИА, включающего планетарную передачу, мальтийский и кривошипно-ползунный механизмы.

4. Выполнить динамический анализ КИА с целью выбора электродвигателя и определения момента инерции маховика.

5. Произвести расчеты элементов механизмов КИА.

6. Выполнить графическую часть.

7. Оформить пояснительную записку.

Ниже приводятся методические указания к выполнению курсового проекта (курсовой работы).

СТРУКТУРНЫЙ АНАЛИЗ

При структурном анализе выявляются и исключаются избыточные связи, которые могут привести к неработоспособности конструкции. Анализ выполняется по кинематической схеме, в которой кинематические пары должны быть изображены по ГОСТ с указанием всех геометрических связей, соответствующих виду и классу пар. При анализе не следует учитывать так называемые локальные связи. Например, если в реальной конструкции вал устанавливается на двух опорах, то при структурном анализе по кинематической схеме необходимо считать, что вал образует со стойкой вращательную пару 5-го класса.

При нумерации звеньев на кинематической схеме рекомендуется обозначить ведущее звено первым, а стойку – последним номером. Для обозначения кинематических пар рекомендуется использовать заглавные буквы латинского алфавита.

В тексте пояснительной записки следует перечислить все звенья с указанием наименований элементов, входящих в эти звенья, все кинематические пары с указанием вида и класса. Затем необходимо определить степень подвижности по формуле Чебышева

где – число подвижных звеньев; – число кинематических пар соответственно 5-го и 4-го классов.

Примеры составления кинематических схем и структурного анализа механизмов приведены в [1], с.23...41; [3], с.14...21; [4], с.28...52.

Мальтийского механизма

Перед построением планов скоростей и ускорений необходимо изобразить мальтийский механизм в выбранном масштабе.

Построение следует выполнить для трех положений мальтийского механизма:

а) для момента входа цевки кривошипа в паз креста, т.е. при ;

б) для момента поворота кривошипа на ¼ рабочего угла, т.е. при ;

в) для момента поворота кривошипа на ½ рабочего угла, т.е. когда ось кривошипа совмещается с линией, соединяющей оси валов 4 и 5.

При построении планов скоростей и ускорений считаются заданными угловая скорость , угол рабочего поворота вала кривошипа , число пазов креста , межосевое расстояние и длина кривошипа .

Используя результаты построения планов необходимо определить угловые скорости и угловые ускорения вала креста для указанных выше трех положений.

В качестве примера рассмотрим построения планов скоростей и ускорений для положения кривошипа, изображенного на рис.7, а.

Будем рассматривать точку В как точку, принадлежащую одновременно кривошипу и кресту. Движение точки В, принадлежащей кривошипу, считаем абсолютным. Точка В, принадлежащая кресту находится в сложном движении – в переносном вращательном с крестом и относительном прямолинейном вдоль паза креста.

Построение планов скоростей ведем по следующему векторному уравнению:

где – вектор абсолютной скорости точки В, равный по модулю и направленный перпендикулярно АВ; – вектор переносной скорости точки В, равный по модулю и направленный перпендикулярно ВС; – вектор относительной скорости точки В, направленный параллельно ВС.

Выполним построение плана скоростей при положении кривошипа, когда он повернулся на ¼ рабочего угла. От полюса (рис.7, б) отклады-

а)

б) в)

Рис.7

ваем от резок , изображающий в определенном масштабе вектор скорости . При этом , причем если изменяется в м/c, то масштабный коэффициент – в . ( показывает, сколько единиц скорости приходится на 1 мм отрезка ). Затем из точки проведем прямую перпендикулярно ВС, а через точку b –прямую параллельно ВС. Точка их пересечения k является концом вектора и началом вектора . Определим модуль вектора из плана с учетом масштабного коэффициента , т.е. (м/c). Так как скорость зависит от угловой скорости креста, то величина угловой скорости (1/c). Здесь – расстояние от точки В до центра вращения креста в м.

При построении плана скоростей для первого положения мальтийского механизма следует иметь в виду, что , а для третьего положения – .

Строим план ускорений мальтийского механизма. При рассмотрении ускорения точки В, принадлежащей кресту, следует учесть, что при переносном вращательном движении и относительном перемещении вдоль паза возникает также ускорение Кориолиса. Поэтому построение плана ускорений ведем по следующему уравнению

,

где – вектор абсолютного ускорения, равный нормальному ускорению точки В (при ), принадлежащей кривошипу, равный по модулю и направленный по АВ от точки В к точке А; – вектор нормального ускорения в переносном вращательном движении точки В, принадлежащей кресту, равный по модулю и направленный от точки В к точке С; – вектор касательного ускорения в переносном движении, направленный перпендикулярно СВ; – вектор относительного ускорения точки В, направленный вдоль паза креста по СВ; – вектор ускорения Кориолиса, равный по модулю и имеющий направление вектора , повернутого на в направлении угловой скорости (см. рис.7, а, в).

Выполним построение плана ускорений по векторному уравнению, в котором известны векторы по направлениям и модулям. Для векторов известны лишь линии их действия.

От полюса откладываем отрезок , который изображает на плане в определенном масштабе вектор . Масштабный коэффициент ускорений . показывает, сколько единиц ускорения в приходится на 1мм отрезка . Далее из полюса строим отрезок , изображающий вектор в том же масштабе, и через точку п проводим отрезок пк перпендикулярно , который изображает вектор ускорения Кориолиса . Так как известны линии действия векторов , то через точку к проводим прямую, параллельную СВ, а через точку b – прямую, перпендикулярную СВ. Точка их пересечения r дает конец вектора и начало вектора .

Определим модуль вектора из плана с учетом масштабного коэффициента, т.е. ( ). Затем вычислим угловое ускорение

( ).

При построении плана ускорений для первого положения мальтийского механизма обратим внимание на то, что , , и что для третьего положения , , .

Методика построения планов скоростей и ускорений звеньев механизмов приведена в [1], с.70...72, 75...80; [3], с.33...38; [4], с.79...96.

6.2. Кинематический анализ планетарной передачи

При проектировании планетарной передачи выбирается схема, число сателлитов к, передаточное отношение и модуль зацепления т (для всех заданий следует принять ).

Условия проектирования

При проектировании передачи необходимо удовлетворить следующим требованиям:

1. возможности размещения нескольких сателлитов с зазорами между ними (условию соседства);

2. соосности входного и выходного валов передачи (условию соосности);

3. возможности установки нескольких сателлитов при сборке при условии их нормального зацепления с центральными колесами (условию сборки).

Кроме того, в зависимости от вида кинематической схемы могут быть дополнительные требования (получение наименьших габаритных размеров, наибольших передаточных отношений и др.).

Условие соседства нескольких сателлитов будет выполнено, если

, (3)

где – диаметр окружности выступов венца сателлита, – расстояние между осями центрального колеса и сателлита, мм.

Условие соосности входного и выходного валов передачи при одинаковых модулях зацепления и колесах, изготовленных без смещения исходного контура, будет выполнено, если:

1. – для передачи на рис.1;

2. – для передачи на рис.2; (4)

3. – для передачи на рис.3;

4. , – для передачи на рис.4.

Здесь – числа зубьев соответственно колес а, b, f, q.

Условие сборки будет обеспечено в передачах, изображенных на рис.1, 2, 3, если конструктивно сделать так, что относительное положение двух зубчатых колес каждого сателлита устанавливается независимо друг от друга при монтаже.

В передаче, изображенной на рис.4, для обеспечения условия сборки необходимо или чтобы числа зубьев колес и в каждой ступени были кратны числу сателлитов к, или чтобы равнялось целому числу.

Выбор числа зубьев

1. Передаточное отношение передачи с ведущим водилом (рис.1) определяется по формуле

. (5)

Если принять , то для обеспечения соосности и минимальных габаритов рекомендуется .

Так как передаточное отношение простой передачи (при оставленном водиле н)

, (6)

то подставляя в (6) числа зубьев , выраженные через z, получим уравнение

. (7)

Решая это уравнение, после подстановки заданного значения определим z. Из двух значений z после округления до целого числа следует принять наибольшее.

2. Передаточное отношение передачи с ведущим центральным колесом а (рис.2) определяется по формуле

. (8)

Если принять , то на основании условия соосности числа зубьев колес b и q определяются по формулам

, .

После вычисления и их следует округлить до целых значений (соблюдая условие соосности).

3. Передаточное отношение передачи с ведущим водилом (рис.3) определяется по формуле

. (9)

Так как , то

. (10)

Для получения рациональных габаритных размеров передачи при рекомендуется принять , . На основании условия соосности в этом случае . При заданном значении после подстановки принятых значений и в формулу (9) определим значение .

С целью уточнения заданного передаточного отношения планетарной передачи рекомендуется изменять числа зубьев колес в числителе и знаменателе выражений (5), (6), (8) и (9), не забывая проверять условие соосности.

4. В двухступенчатой передаче, изображенной на рис.4, рекомендуется принять , , . Тогда передаточное отношение передачи с ведущим центральным колесом равно

, (11)

откуда

Принимая (желательно, чтобы было кратно числу сателлитов), предварительно определим

Для обеспечения сборки необходимо уточнить число зубьев так, чтобы оно было либо кратно числу сателлитов, либо равнялось целому числу.

Число зубьев сателлита определяется из условия соосности по формуле . После округления до целого числа необходимо уточнить и , соблюдая условие соосности и условие равенства целому числу.

Отклонение полученного передаточного отношения после уточнения чисел зубьев колес в указанных передачах не должно превышать 3...5% от заданного.

5. После выбора чисел зубьев необходимо определить основные размеры планетарной передачи:

Межосевые расстояния

(для схем на рис. 1, 2, 4),

(для схемы на рис. 3),

диаметры делительных окружностей колес ,

(здесь m – модуль зацепления, z – число зубьев соответствующего колеса),

диаметры окружностей выступов колес .

На основании полученных данных следует проверить условие соседства нескольких сателлитов (по формуле 3) и условие соосности входного и выходного валов передачи (по формулам 4).

Кинематический анализ, метода расчета параметров и выбора чисел зубьев колес планетарных передач приведены в [1], с. 406...410, 413...426; [3], с. 241...246, 252...255; [4], с. 154...166.

6.2.3. Построение плана скоростей планетарной передачи

Построение плана скоростей выполняется при заданной угловой скорости ведущего звена и известных геометрических размерах планетарной передачи. По планам скоростей определяются угловые скорости ведомого звена и сателлита.

Перед построением планов скоростей следует изобразить кинематическую схему планетарной передачи в выбранном масштабе.

Допускается строить план скоростей с изображением одного сателлита и центральных колес.

На рис.8 изображена схема планетарной передачи с ведущим центральным колесом а.

Сначала строим план линейных скоростей колес и водила. Для этого на вертикальную линию, изображенную справа от схемы, переносятся характерные точки О, Р, , Q. Точки Р и Q совпадают с полюсами

зацеп

ления. Точка

совмещена с осью сателлита.

Рис.8

12	Поделиться: