Простой процент: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.

Простой процент: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.

Простой процент определяется как произведение капитала, процентной ставки и времени: 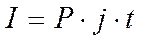, где P – первоначальный капитал, j – номинальная годовая процентная ставка, t – срок депозита (в годах), I – простой процент (в денежном выражении). Сумма первоначального капитала и наросшего процента называется наращенной суммой (S). Итак, . Наращенную сумму часто обозначают FV. 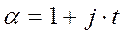Коэффициент наращения показывает наращенную сумму в расчете на одну денежную единицу первоначального капитала (a.) .Приведенной (текущей) стоимость -первоначальный капитал, обеспечивающий наращенную сумму S, обозначают PV= Коэффициентом дисконтирования показывает текущую стоимость одной денежной единицы наращенной суммы, т.е. то количество денег, которое нужно положить на счет в настоящий момент времени для того, чтобы обеспечить одну денежную единицу наращенной суммы. Обозначаем буквой d. Итак, .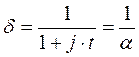

Сложный процент: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.

Процент называется сложным, когда после начисления процента начальный капитал вместе с наросшим процентом снова кладется на счет в банке, в следующем периоде времени процент нарастает не только с первоначального капитала, но также и с процента, наросшего в первом периоде. Наращенная сумма, . Время между двумя последовательными капитализациями (начислениями) процента называется периодом капитализации процента , m- число капитализаций процента в течение года. Коэффициент наращения a (показывающий наращенную сумму в расчёте на одну денежную единицу первоначального капитала), находится по формуле: 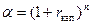. Текущая стоимость – это первоначальный капитал, обеспечивающий заданную наращенную сумму. . Коэффициент дисконтирования d (показывающий текущую стоимость в расчете на одну денежную единицу наращенной суммы). .

 

Смешанный метод начисления процентов при нецелом числе периодов капитализации: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.

В соответствии со смешанным методом, вначале нужно найти наращенную сумму для целого числа периодов капитализации в сроке депозита. (Здесь через 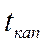обозначен срок депозита, выраженный в периодах капитализации. Заметим, что .) Эта сумма находится по формуле для сложного процента: 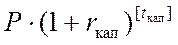. Затем, для оставшейся дробной части срока депозита 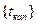начисляется простой процент с капитала (наросшего за целое число периодов капитализации ). Заметим, что 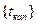периода капитализации – это года. Следовательно, к концу срока депозита наращенная сумма составит: 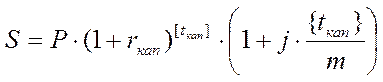. Учитывая, что , формулу можно также записать в виде: .

 

Общий метод начисления процентов при нецелом числе периодов капитализации: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.

В соответствии с общим методом, наращенная сумма ищется по формуле , где- S наращенная сумма, Р- первоначальный капитал, , m- число капитализаций процента в течение года.

 

Эквивалентные процентные ставки: экономический смысл, критерий эквивалентности.

Две номинальные годовые процентные ставк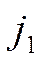и и (с числом капитализаций процента в году и , соответственно) называются эквивалентными, если при одном и том же начальном капитале они обеспечивают одинаковый процент за равные промежутки времени. При конечных и условие эквивалентности номинальных годовых процентных ставок и запишется следующим образом: , в случае, если , 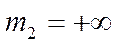условие эквивалентности имеет вид: .

Стоимость последовательности платежей в произвольный момент времени: экономический смысл и нахождение.

Стоимость последовательности платежей в произвольный момент времени будем понимать количество денег, которое обеспечивается заданной последовательностью платежей в момент времени . , (10) где r – эффективная процентная ставка для периодов времени, в которых выражены сроки платежей .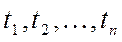

Простой процент: наращенная сумма, текущая стоимость, коэффициенты наращения и дисконтирования.

Простой процент определяется как произведение капитала, процентной ставки и времени: 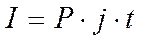, где P – первоначальный капитал, j – номинальная годовая процентная ставка, t – срок депозита (в годах), I – простой процент (в денежном выражении). Сумма первоначального капитала и наросшего процента называется наращенной суммой (S). Итак, . Наращенную сумму часто обозначают FV. 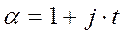Коэффициент наращения показывает наращенную сумму в расчете на одну денежную единицу первоначального капитала (a.) .Приведенной (текущей) стоимость -первоначальный капитал, обеспечивающий наращенную сумму S, обозначают PV= Коэффициентом дисконтирования показывает текущую стоимость одной денежной единицы наращенной суммы, т.е. то количество денег, которое нужно положить на счет в настоящий момент времени для того, чтобы обеспечить одну денежную единицу наращенной суммы. Обозначаем буквой d. Итак, .

1234	Поделиться:

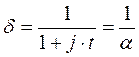Популярное:

1. Измерение АЧХ передаточной функции простой цепи
2. Коэффициенты к ресурсным элементным сметным нормам
3. Коэффициенты распределения второго этапа (ставки драйверов операций)
4. Коэффициенты регрессии. Линии регрессии.
5. Коэффициенты финансово-хозяйственной деятельности должника и показатели, используемые для их расчета
6. Матрицы. Сумма, произведение на число, произведение матриц.
7. Моменты инерции тел простой геометрической формы
8. Номинальная ставка процента - это текущая рыночная ставка, не учитывающая уровень инфляции.
9. Организация производства (понятие, принципы). Коэффициенты наращивания и дисконтирования, их использование при проведении разновременных затрат.
10. Показатели размера и интенсивности вариации (размах, среднее линейное отклонение, простое и взвешенное стандартное отклонение, дисперсия для выборки и ГС, коэффициенты осцилляции и вариации).
11. Предложение капитала. Текущая дисконтируемая стоимость, ставка процента и фактор времени. Текущее и будущее потребление.