Форвардные доходности облигаций: нахождение и экономический смысл.
Под форвардной доходностью 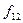 понимают такое значение доходности
понимают такое значение доходности 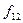 , при котором первая и вторая инвестиционная стратегии обеспечивают одинаковый доход в конце второго года, т.е. при котором
, при котором первая и вторая инвестиционная стратегии обеспечивают одинаковый доход в конце второго года, т.е. при котором  . Итак, форвардная доходность
. Итак, форвардная доходность 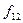 определяется из уравнения (4. Решив это уравнение, получим:
определяется из уравнения (4. Решив это уравнение, получим:  . В случае, если на финансовом рынке отсутствуют бескупонные облигации, то при определении форвардной доходности используются доходности синтетических бескупонных облигаций (чистые доходности).
. В случае, если на финансовом рынке отсутствуют бескупонные облигации, то при определении форвардной доходности используются доходности синтетических бескупонных облигаций (чистые доходности).
Данное выше определение форвардной доходности 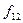 естественным образом обобщается на случай
естественным образом обобщается на случай  . А именно, форвардная доходность
. А именно, форвардная доходность  – это такое значение доходности бескупонных облигаций со сроком погашения в конце периода времени n, найденная с помощью рыночной цены таких облигаций в начале периода
– это такое значение доходности бескупонных облигаций со сроком погашения в конце периода времени n, найденная с помощью рыночной цены таких облигаций в начале периода  , которое обеспечивает одинаковые доходы для следующих двух инвестиционных стратегий:
, которое обеспечивает одинаковые доходы для следующих двух инвестиционных стратегий:
1) Вложить деньги в бескупонные облигации со сроком погашения в конце периода n.
2) Вложить деньги в бескупонные облигации со сроком погашения в конце периода k. Затем, в начале периода  реинвестировать доход в бескупонные облигации со сроком погашения в конце периода n.
реинвестировать доход в бескупонные облигации со сроком погашения в конце периода n.
В соответствии с данным определением, форвардная доходность  находится из уравнения:
находится из уравнения:
 , где
, где  – доходность бескупонных облигаций со сроком погашения в конце периода k, а
– доходность бескупонных облигаций со сроком погашения в конце периода k, а 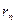 – доходность бескупонных облигаций со сроком погашения в конце периода n.
– доходность бескупонных облигаций со сроком погашения в конце периода n.
В случае, если на финансовом рынке отсутствуют бескупонные облигации, то при определении форвардной доходности используются доходности синтетических бескупонных облигаций (чистые доходности). Решив уравнение, получим:  . Иногда при определении форвардных доходностей удобно использовать аппарат, разработанный в случае непрерывной капитализации процента. Дадим определение (непрерывно капитализируемой) форвардной доходности
. Иногда при определении форвардных доходностей удобно использовать аппарат, разработанный в случае непрерывной капитализации процента. Дадим определение (непрерывно капитализируемой) форвардной доходности  . Форвардная доходность
. Форвардная доходность  – это такое значение (непрерывно капитализируемой) доходности бескупонных облигаций со сроком погашения в момент времени T, найденная с помощью рыночной цены таких облигаций в момент времени
– это такое значение (непрерывно капитализируемой) доходности бескупонных облигаций со сроком погашения в момент времени T, найденная с помощью рыночной цены таких облигаций в момент времени  , которое обеспечивает одинаковые доходы для следующих двух инвестиционных стратегий:
, которое обеспечивает одинаковые доходы для следующих двух инвестиционных стратегий:
3) Вложить деньги в бескупонные облигации со сроком погашения в момент времени T.
4) Вложить деньги в бескупонные облигации со сроком погашения в момент времени  и реинвестировать доход (полученный в момент времени
и реинвестировать доход (полученный в момент времени  ) в бескупонные облигации со сроком погашения в момент времени T.
) в бескупонные облигации со сроком погашения в момент времени T.
В соответствии с данным определением, форвардная доходность  находится из уравнения:
находится из уравнения:
 , где
, где 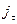 – непрерывно капитализируемая доходность бескупонных облигаций со сроком погашения в момент времени
– непрерывно капитализируемая доходность бескупонных облигаций со сроком погашения в момент времени  , а
, а  – непрерывно капитализируемая доходность бескупонных облигаций со сроком погашения в момент времени T. Очевидным образом уравнение (48) сводится к следующему уравнению:
– непрерывно капитализируемая доходность бескупонных облигаций со сроком погашения в момент времени T. Очевидным образом уравнение (48) сводится к следующему уравнению:  .Решив это уравнение, получим:
.Решив это уравнение, получим:  .
.
Продолжительность портфеля облигаций (вывод формулы).
Поскольку портфель облигаций выплачивает последовательность платежей, продолжительность портфеля облигаций находится по формуле (12) главы 2, т.е.  , (1) где wk – доля текущей стоимости k-го платежа портфеля в текущей стоимости портфеля,
, (1) где wk – доля текущей стоимости k-го платежа портфеля в текущей стоимости портфеля,  – срок выплаты k-го платежа портфеля, n – количество платежей портфеля. Докажем, что для продолжительности портфеля облигаций справедлива формула:
– срок выплаты k-го платежа портфеля, n – количество платежей портфеля. Докажем, что для продолжительности портфеля облигаций справедлива формула:  , (2) где wi – доля текущей стоимости облигаций i-го вида в текущей стоимости портфеля,
, (2) где wi – доля текущей стоимости облигаций i-го вида в текущей стоимости портфеля,  – продолжительность облигации i-го вида, m – количество видов облигаций в портфеле. Введем следующие обозначения.
– продолжительность облигации i-го вида, m – количество видов облигаций в портфеле. Введем следующие обозначения.
 – количество облигаций i-го вида в портфеле,
– количество облигаций i-го вида в портфеле,  – текущая стоимость k-го платежа облигации i-го вида,
– текущая стоимость k-го платежа облигации i-го вида,  – текущая стоимость облигации i-го вида,
– текущая стоимость облигации i-го вида,  – текущая стоимость k-го платежа портфеля,
– текущая стоимость k-го платежа портфеля,  – текущая стоимость портфеля,
– текущая стоимость портфеля,  – доля текущей стоимости k-го платежа облигации i-го вида в текущей стоимости облигации i-го вида.
– доля текущей стоимости k-го платежа облигации i-го вида в текущей стоимости облигации i-го вида.
Очевидно, что имеют место следующие формулы:
 ,
,  ,
,  ,
, 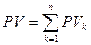 (3)
(3)
 ,
,  ,
,  ,
, 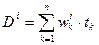 . (4)
. (4)
С учетом формул (3)-(4), имеем


Таким образом, мы доказали формулу (2).
Популярное:

