Гибкая нить (провода, канаты, цепи, ремни).

РАБОЧАЯ ТЕТРАДЬ

 

дисциплины «Техническая механика»

Для студентов- заочников образовательных учреждений

среднего профессионального образования по специальностям:

13.02.11 - Техническая эксплуатация и обслуживание электрического и электромеханического оборудования (по отраслям);

18.02.09 – Переработка нефти и газа;

21.02.01 – Разработка и эксплуатация нефтяных и газовых месторождений;

21.02.02 – Бурение нефтяных и газовых месторождений;

21.02.03 – Сооружение и эксплуатация газонефтепроводов и газонефтехранилищ;

22.02.06 – Сварочное производство;

21.02.11 – Геофизические методы поисков и разведки месторождений полезных ископаемых.

 

Пермь 2014 г

В рабочей тетради приведены задания, отражающие темы типовой программы дисциплины «Техническая механика». Материал изложен в порядке изучения данных тем. Представленные задания способствуют изучению и закреплению знаний в областях теоретической механики, сопротивления материалов и деталей машин, которые необходимы учащимся при дальнейшей работе на производстве.

В начале каждой темы приведены теоретические основы, затем задача на закрепление материала. Многие задания в данной тетради направлены на развитие технического мышления, способствуют развитию навыков работы с технической литературой.

Рабочая тетрадь предназначена для организации самостоятельной работы учащихся учреждений среднего профессионального образования и проведения контроля их знаний преподавателем.

 

Содержание

1. Аннотация_________________________________________2

2. Содержание________________________________________3

3. Статика _________________________________________4-19

4. Кинематика________________________________________20-23

5. Динамика _________________________________________24-28

6. Сопротивление мвтериалов___________________________29-47

Статика:

Вопросы для самоконтроля

1. Назовите разделы теоретической механики и укажите, какие вопросы в них изучают.

Разделы теоретической механики, кинематика, статика, динамика.В них изучают вопросы: Кинематика – часть механики, в которой изучаются зависимости между величинами, характеризующими состояние движения систем, но не рассматриваются причины, вызывающие изменение состояния движения.Статика – это учение о равновесии совокупности тел некоторой системы отсчета.Динамика – часть механики, в которой рассматривается влияние сил на состояние движения систем материальных объектов.

2. Дайте определение материи. Перечислите формы движения материи.

Материя характеризуется такими атрибутами, как: движение, пространство, время, отражение, структурность (внутренняя расчленённость реального мира), системность, взаимодействие, самоорганизация. Физическая и химическая форма движения, биологическая, социальная форма движения. Пять основных форм движения материи, которые соответствуют основным структурным уровням и формам материи:

- Механическое движение – перемещением тел в пространстве;

- Физическое (по существу тепловое) – движение молекул;

- Химическое – движение атомов внутри молекул.

- Органическое или биологическое – развитием белковой формы жизни.

- Социальное движение – все изменения в обществе.

Эта классификация к настоящему времени устарела. В частности, сейчас неправомерно физическое движение сводить только к тепловому. Поэтому современная классификация форм движения материи включает:

- пространственное перемещение (квантово-механическое);

- электромагнитное движение, определяемое как взаимодействие заряженных частиц;

- гравитационную форму движения; сильное (ядерное) взаимодействие;

- слабое взаимодействие (поглощение и излучение нейтрона);

- химическую форму движения (процесс и результат взаимодействия молекул и атомов);

- геологическую форму движения материи (связанную с изменением в геосистемах - материках, слоях земной коры и т. д.);

- космическая форма движения, изучаемая астрофизикой;

- биологическую форму движения (обмен веществ, процессы, происходящие на клеточном уровне, наследственность и т. д.;

- социальную форму движения (процессы, происходящие в обществе).

 

3. В чем общность понятий абсолютно твердого тела и материальной точки и в чем их различие?

Неизменяемая механическая система, состоящая из континуума материальных точек, называется абсолютно твердым телом.

Материальная точка- это часть материи, достаточно малая для того, чтобы в любой момент

времени можно было определить ее положение в абсолютном пространстве как положение

объекта, не имеющего геометрических размеров.

 

4. Дайте определение силы.

 

СИЛА - векторная физическая величина, равная произведению массы тела, на сообщаемое этой силой ускорение. Применяется для описания механического воздействия на данное тело со стороны других тел, приводящего к изменению характера движения тела или его деформации.

5. Какие системы сил называют статически эквивалентными?

 

Эквивалентные системы сил - системы сил, оказывающие одинаковое механическое действие на одно и то же тело.

6. Что такое равнодействующая система сил, уравновешивающая сила?

 

Уравновешенная система сил - система сил, под действием которой те-ло находится в равновесии.
Уравновешивающей силой- сила, равная по модулю равнодействующей и направленная по линии ее действия в противоположную сторону.

 

7. Сформулируйте аксиомы статики.

 

Аксиома 1.Две силы, действующие на абсолютно твердое тело уравновешива-ются только тогда, когда они равны по величине и направлены по од-ной прямой в противоположные стороны.

Аксиома 2. Действие данной системы сил на абсолютно твердое тело не изме-нится, если прибавить к ней или отнять от нее уравновешенную сис-тему сил.

Аксиома 3 Равнодействующая двух сил, приложенных к АТТ в одной точке, равна их геометрической сумме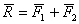 , т.е. выражается по моду-лю и направлению диагонали параллелограмма, построенного на этих силах.Аксиома 4 Всякому действию одного тела на другое соответствует равное по величине, но противоположное по направлению противодействие. Действие и противодействие-это силы, приложенные к двум раз-личным телам, поэтому они не уравновешиваются. Аксиома 5 Если деформируемое тело под действием системы сил находится в равновесии, то при отвердевании его равновесие сохраняется. Под действием сил тело D находится в равновесии. Если трос CB заменить стержнем, то равновесие не нарушится, равновесие не нарушится и в том случае, если трос BD за-менить стержнем, если же стержень АВ заменить тросом - равновесие нарушится.

 

8. Какие тела называются свободными, а какие несвободными?

 

Тело, которое может совершать из данного положения любые перемещения в пространстве, называется свободным.

Тело, перемещениям которого препятствуют какие-нибудь другие, скрепленные или соприкасающиеся с ним тела, называется несвободным.

 

 

9. Что называется связью?

 

Тело называется свободным, если его перемещения в пространстве ничем не ограничены. Если на перемещение точек тела накладываются ограничения, то тело называется несвободным или связанным. Материальные тела, ограничивающие перемещения данного тела называются связями. Сила, с которой связь действует на данное тело, называется реакцией связи. Сила действует на связь, а реакция связи на тело.

10. Что такое реакция связи?

Сила, с которой данная связь действует на тело, препятствующая тем или иным его перемещениям, называется реакцией связи. Реакция связи направлена в сторону противоположную той, куда связь не дает перемещаться телу.

11. Перечислите виды связей и укажите направление соответствующих им реакций.

1.Гладкая плоскость (поверхность) или опора. Реакция N гладкой плоскости (поверхности) или опоры направлена по общей нормали к поверхностям соприкасающихся тел в точке их касания и приложена к этой точке.

Жесткая заделка

Нахождение реакции жесткой заделки сводится к определению составляющих Х_А и Y_A препятствующих линейному перемещению балки в плоскости действия сил, и алгебраической величине момента m_A, препятствующего вращению балки под действием приложенных к ней сил.

 

В результате изучения темы студент должен:

иметь представление об абсолютно твердом теле и материальной точке; о силе равнодействующей и уравновешивающей силах, системах сил;

знать виды связей и их реакции; принцип освобождения от связей.

Тема 1.2. Плоская система сходящихся сил
Эта система эквивалентна одной силе (равнодействующей) и стремится придать телу (в случае, если точка схождения сил совпадает с центром тяжести тела) прямо­линейное движение. Равновесие тела будет иметь место в случае равенства равнодей­ствующей нулю. Геометрическим условием равновесия является замкнутость много­угольника, построенного на силах системы, аналитическим условием — равенство нулю алгебраических сумм проекций сил системы на любые две взаимноперпендикулярные оси. Следует научиться решать задачи на равновесие тел, обратив особое внимание на рациональный выбор направления координатных осей.

 

Вопросы для самоконтроля

1. Геометрический способ нахождения равнодействующей плоской системы схо­дящихся сил.

Тема 1.3. Пара сил

Система пар сил эквивалентна одной паре (равнодействующей) и стремится при­дать телу вращательное движение. Равновесие тела будет иметь место в случае равен­ства нулю момента равнодействующей пары. Аналитическим условием равновесия является равенство нулю алгебраической суммы моментов пар системы. Следует об­ратить особое внимание на определение момента силы относительно точки. Необхо­димо помнить, что момент силы относительно точки равен нулю лишь в случае, если точка лежит на линии действия силы.

Вопросы для самоконтроля
1. Что такое пара сил?

Парой сил называются две равные и параллельные силы, не лежащие на одной прямой и направленные в противоположные стороны. Пара сил имеет важное значение в практике. Так, водитель автомобиля, передавая руками усилия на рулевое колесо, использует пару сил.

2. Что такое момент пары сил, плечо пары сил?

 

Пара сил оказывает вращающее действие, которое может быть оценено моментом пары.

Моментом пары называется вектор с такими признаками:

• он перпендикулярен плоскости пары;
• направлен в ту сторону, откуда вращение, которое осуществляет пара, видно против часовой стрелки;
• его модуль равняется произведению модуля одной из сил пары на плечо пары с учетом знака

 

M(F₁, F₂ ) = F₁h = F₂h

 

где h – плечо пары - расстояние между линиями действия сил пары, т.е. длина перпендикуляра, проведенного из произвольной точки линии действия одной из сил пары на линию действия второй силы.

Момент пары считается положительным, если силы пары стремятся повернуть плоскость, в которой они расположены, против хода часовой стрелки (рисунки 1.1, 1.2 – моменты этих пар сил положительны).

Момент пары сил может быть определен как векторная величина:

M(F₁, F₂ ) = AB⊗ F₂ = BA⊗ F₁

 

т.е. вектор M(F₁, F₂ ) всегда перпендикулярен плоскости, в которой расположена пара сил, и его направление определяется правилом векторного произведения

Поскольку действие пары сил оценивается величиной и направлением вращающего момента, то на плоскости пару сил изображают в любом месте твердого тела, задавая величину и направление вращающего действия (см. на рисунке 1.4 изображение пар сил M₁ и M₂ ).

3. Сформулируйте условие равновесия системы пар сил.

 

Если на твердое тело действует несколько пар сил, как угодно расположенных в пространстве, то последовательно применяя правило параллелограмма к каждым двум моментам пар сил, можно любое количество пар сил заменить одной эквивалентной парой сил, момент которой равен сумме моментов заданных пар сил.
В результате изучения темы студент должен:
иметь представление о вращающем действии пары сил на тело и ее характеристиках; о свойствах пары сил; моменте пары сил;
знать условия равновесия пары сил.
Тема 1.4. Плоская система произвольно расположенных сил
Эта система эквивалентна одной силе (называемой главным вектором) и самой паре (момент, который называют главным моментом) и стремится придать телу в общем случае прямолинейное и вращательное движение одновременно. Изученные ранее системы сходящихся сил и система пар — частные случаи произвольной систе­мы сил. Равновесие тела будет иметь место в случае равенства нулю и главного век­тора, и главного момента системы. Аналитическими условиями равновесия является равенство нулю алгебраической суммы проекций сил системы на оси Х, У, и равенство нулю суммы моментов всех сил относительно любой точки. Следует научиться ре­шать задачи на равновесие тел, в том числе на определение опорных реакций балок и сил, нагружающих стержни, обратив особое внимание на рациональный выбор направления координатных осей и положения центра моментов.

Вопросы для самоконтроля

1. Что такое момент силы относительно точки? Как берется знак момента силы относительно точки? Что называется плечом силы?

 

Моментом силы относительно точки называется векторное произведение радиус-вектора точки приложения силы на вектор силы. Относительно точки (в механике) - кратчайшее расстояние от данной точки ( центра) до линии действия силы, т. е. длина перпендикуляра, опущенного из этой точки на линию действия силы.
2. В каком случае момент силы относительно точки равен нулю?

Если сила и ось лежат в одной плоскости, то момент силы относительно этой оси равен нулю.

 

3. Что такое главный вектор и главный момент плоской системы сил?

Главным вектором системы сил называется вектор R, равный векторной сумме этих сил:

R = F ₁ + F ₂ +... + F _n = F _i.

Для плоской системы сил ее главный вектор лежит в плоскости действия этих сил.

Главным моментом системы сил относительно центра O называется вектор L _O, равный сумме векторных моментов этих сил относительно точки О:

L _O = M _O( F ₁) + M _O( F ₂) +... + M _O( F _n) = M _O( F _i).

 

4. Сформулируйте теорему Вариньона.

 

согласно теореме момент равнодействующей системы сил относительно какого-либо центра равен геометрической сумме моментов составляющих систему сил относительно того же центра.

 

5. Сформулируйте аналитическое условие равновесия плоской системы произ­вольно расположенных сил.

для равновесия плоской системы произвольно расположенных сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на оси координат x и y равнялись нулю, и чтобы алгебраическая сумма моментов этих сил относительно любой точки плоскости также равнялась нулю.

Условие равновесия упрощенно запишем в виде равенств:

Σ X = 0; Σ Y = 0; Σ M = 0.

6. Укажите три вида уравнения равновесия плоской системы произвольно рас­положенных сил.

Математически условие равновесия пространственной системы произвольно расположенных сил можно записать в виде уравнений:

· Σ X = 0; Σ Mx(Fi) = 0;

· Σ Y = 0; Σ My(Fi) = 0;

· Σ Z = 0; Σ Mz(Fi) = 0.

7. Укажите, как рационально выбрать направления осей координат и центр мо­ментов.

В качестве центра моментов рекомендуется выбрать точку, где пересекаются две неизвестные силы; уравнение моментов относительно этой точки будут содержать только одну неизвестную. Направление координат осей x и y следует выбрать так чтобы оси были перпендикулярны некоторым неизвестным силам.
8. Какие нагрузки называются сосредоточенными и распределенными?

Сила не может быть приложена к точке, поскольку точка - безразмерная, бесконечно малая единица пространства, поэтому фактически силы воздействуют на очень малую площадку, размерами которой пренебрегают. Такие силы называют сосредоточенными.

часто встречаются силы, приложенные не к точке, а к объему или поверхности тела, например сила тяжести, давления ветра, воды и т. п., т. е. нагрузку воспринимает не бесконечно малая площадка, а значительная площадь или объем тела. Такие силы называют распределенными.

9. Что такое интенсивность равномерно распределенной нагрузки?

Распределенная нагрузка, имеющая постоянную интенсивность по всей длине участка называется равномерно распределенной
10. Как найти числовое значение, направление и точку приложения равнодей­ствующей равномерно распределенной нагрузки?

При решении задач статики распределенную нагрузку заменяют ее равнодействующей. Модуль равнодействующей равномерно распределенной нагрузки равен Q = ql

11. Какие системы называются статически определимыми?

Статически определимой системой понимается такая система, для которой усилия во всех ее элементах могут быть определены с применением лишь уравнений равновесия.
12. Что называется силой трения?

Силами трения называют силы, возникающие при соприкосновении поверх-ностей двух тел или частей одного тела и препятствующие их взаимному пере-мещению. Они приложены к телам (или к их частям) вдоль поверхности сопри-косновения и всегда направлены в сторону, противоположную относительной скорости движения.

13. Перечислите основные законы трения скольжения.

Й закон Кулона

Cила трения не зависит от величины площади трущихся поверхностей.

Первый закон можно объяснить с помощью следующих умозаключений. Если площадь трущихся поверхностей увеличится, то увеличится и количество сцепляющихся неровностей, но уменьшится давление на опорную поверхность, которое обратно пропорционально площади контакта тел. Поэтому сопротивление относительному перемещению останется прежним.

Й закон Кулона

Максимальная сила трения прямо пропорциональна нормальной составляющей внешних сил, действующих на поверхности тела. Второй закон Кулона говорит о том, что если увеличится нормальная составляющая внешних сил, действующих на поверхности тела (иначе говоря, увеличится сила нормального давления или реакции), то во столько же раз возрастет максимальная сила трения.

Й закон Кулона

Сила трения зависит от материала тел, состояния трущихся поверхностей и рода смазки.

Согласно третьему закону трения скольжения, коэффициент трения скольжения зависит от материалов трущихся тел, качества обработки их поверхности (степени шероховатости), рода и температуры смазки. В зависимости от наличия между сопрягаемыми поверхностями слоя смазки трение подразделяется на два вида: трение без смазочного материала (сухое трение) и трение в условиях смазки.

14. Что такое угол трения, конус трения?

Рассмотрим твердое тело на шероховатой поверхности (рисунок 2.2), находящееся под действием активных сил в предельном состоянии равновесия, т.е. когда сила трения достигает своего наибольшего значения при данном значении нормальной реакции.

В этом случае полная реакция шероховатой поверхности отклонена от нормали к общей касательной плоскости трущихся поверхностей на наибольший угол ( R^max ). Этот наибольший угол между полной реакцией, построенной на наибольшей силе трения при данной нормальной реакции и направлением нормальной реакции, называется углом трения φ :

 

tgφ = F_тр^max/N = fN/N = f.

 

 

Рисунок 2.2

Конус трения – поверхность, образованная линией действия максимальной реакции опорной поверхности при движении тела в различных направлениях

 

15. Каковы особенности трения качения?

В большинстве случаев величина трения качения гораздо меньше величины трения скольжения при прочих равных условиях, и потому качение является распространенным видом движения в технике. Трение качения возникает на границе двух тел, и поэтому оно классифицируется как вид внешнего трения.

16. Определение опорных реакций балочных систем

В машинах и конструкциях очень часто встречаются тела удлиненной формы, называемые балками или балочными системами. Балки предназначены, в основном, для восприятия поперечных нагрузок, а балочные системы имеют специальные опорные устройства для сопряжения их с другими элементами и передачи на них усилий. Опоры балок могут быть разделены на три основных типа: шарнирно-подвижные, шарнирно-неподвижные, жесткая заделка. Рассмотрим правило для определения направления реакций связей на них.

Шарнирно-подвижная опора допускает поворот вокруг оси шарнира и линейное перемещение параллельно опорной плоскости. Реакция такой связи будет направлена перпендикулярно опорной плоскости и неизвестна только по модулю.Шарнирно-неподвижная опора допускает только поворот вокруг оси и не допускает никаких линейных перемещений. Реакция такой опоры будет направлена перпендикулярно оси шарнира; модуль и ее направление заранее неизвестны (два неизвестных). В этих случаях при решении задач такую реакцию разлагают на две взаимно перпендикулярные составляющие Xв и Ув, неизвестные по модулю, но известные по направлению. Жесткая заделка (защемление) показана на рис. 5, опора С. Она не допускает ни линейных перемещений, ни поворотов защемленного конца балки. Жесткую заделку заменяют реактивной силой R_c, неизвестной по модулю и направлению и поэтому разлагаемую на две составляющие Х_с и У_с и реактивным моментом т (три неизвестных).

Для заданных балочных систем:

1.Показать реакции, возникающие в опорах А и В под действием внешних сил;

Записать уравнения равновесия для определения балочных опор;

2. Как производится проверка правильности решения?

1.

2. Σ X = 0; Σ Y = 0; Σ M = 0.

2. Решение по схеме а):
3. Σ M_А = F₁*sin45⁰*2*sin45⁰-m+F₂*4-R_B*5=0
4. R_B= (F₁*sin45⁰*2*sin45⁰-m+F₂*4)/5 = (10*0, 71*2*0, 71-10+15*4)/5=12 кН
5. Σ M_В = F₁*sin45⁰*(2*sin45⁰+5)-m+F₂*1-R_А*5=0
6. R_А= (F₁*sin45⁰*(2*sin45⁰+5)-m+F₂*1)/5 = (7, 1*6, 4-10+15)/5=10, 1 кН
7. Проверка:
8. Σ Y = R_А- F₁*sin45⁰-F₂+ R_B=10, 1-7, 1-15+12=0
10. Решение по схеме б):
11. Σ X = F₁*cos45⁰- R_х = 0
12. R_х = F₁*cos45⁰ =10*0, 71=7, 1 кН
13. Σ Y = F₁*sin45⁰+q*3- R_y = 0
14. R_y = F₁*sin45⁰+q*3=10*0, 71+10*3=37, 1 кН
15. R = √ R_х² +R_y² =√ 7, 1² +37, 1²=37, 7 кН
16. Σ M = F₁*sin45⁰*2*sin45⁰+ q*3*5, 5+m-М= 0
17. М= F₁*sin45⁰*2*sin45⁰+ q*3*5, 5+m=10*0, 71*2*0, 71+10*3*5, 5+10=185 кНм
18. Проверка, как правило, не производится.
20. Решение по схеме в):
21. Σ M_А = F₁*2+m+F₂*5-R_B*7=0
22. R_B= (F₁*2+m+F₂*5)/7 = (15*2+30+20*5)/7=22, 9 кН
23. Σ M_В = F₁*5-m+F₂*2-R_А*7=0
24. R_А= (F₁*5-m+F₂*2)/7 = (15*5-30+20*2)/7=12, 1 кН
25. Проверка:
26. Σ Y = R_А- F₁ -F₂+ R_B=12, 1-15-20+22, 9=0

 

В результате изучения темы студент должен:

иметь представление о главном векторе и главном моменте сил; частых случаях приведения силы и системы сил к данному центру; трении и условии самоторможения;
знать определение момента силы относительно точки, виды балочных опор; условия равновесия плоской системы сил; классификацию нагрузок;
уметь определять опорные реакции балочных систем.

 

Тема 1.5. Пространственная система сил
Как плоские, пространственные системы подразделяют на системы сходящихся или произвольно расположенных сил. Многоугольник, построенный на сходящихся силах системы, оказывается пространственным, что делает невозможным примене­ние графического и графоаналитического методов решения. Аналитический метод решения аналогичен изложенному для плоских систем с той лишь разницей, что силы проецируются на три (а не на две) взаимно перпендикулярные оси, а моменты сил определяются относительно этих осей (а не точек). Необходимо помнить, что момент силы относительно оси равен нулю в том случае, когда сила и ось лежат в одной плоскости (т.е. линия действия силы или параллельна оси, или пересекает ее).

^ Вопросы для самоконтроля

1. Напишите уравнения равновесия для пространственной системы сходящихся сил.

Равнодействующая R пространственной системы сходящихся сил приложена в точке пересечения линий действия слагаемых сил и является замыкающей стороной силового многоугольника, построенного на этих силах, т. е.

 

R= Σ F_k (1)

 

В отличие от соответствующей плоской задачи силовой многоугольник не является плоским, т.е. он представляет собой ломаную пространственную линию.

 

Проекции равнодействующей силы R на оси декартовых координат х, у, z равны суммам проекций слагаемых сил па соответствующие оси, т. е.

 

R_x= Σ F_kx , R_y= Σ F_ky, R_z= Σ F_kz (2)

 

Модуль равнодействующей R равен

направляющие косинусы даются формулами:

 

cos(R, ^ i) = R_x / R, cos(R, ^ j) = R_y / R, cos(R, ^ k) = R_z / R (4)

 

Для равновесия пространственной системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы равнодействующая равнялась нулю: R=0, т. е. чтобы силовой многоугольник был замкнут. При этом уравнения равновесия имеют вид

Σ F_kx =0, Σ F_ky =0, Σ F_kz =0

2. Что такое момент силы относительно оси? В каких случаях момент силы отно­сительно оси равен нулю?

Для характеристики вращательного действия силы на тело, закрепленное на оси, служит момент относительно оси – алгебраический момент проекции этой силы на плоскость, перпендикулярную к оси, относительно точки пересечения оси с этой плоскостью

Момент считается положительным, если проекция силы на плоскость, перпендикулярную к оси, стремится вращать тело вокруг положительного направления оси против движения часовой стрелки, и отрицательным, если она стремится вращать тело по движению часовой стрелки:

 

M_z(F) = M_o(F_П) = ±hF_П,

где F_П – вектор проекции силы F на плоскость П, перпендикулярную к оси Oz, точка O – точка пересечения оси Oz с плоскостью П.

 

Свойства момента относительно оси:

1) момент равен нулю, если сила параллельна оси. В этом случае равна нулю проекция силы на плоскость, перпендикулярную оси;

2) момент равен нулю, если линия действия силы пересекается с осью. В этом случае равно нулю плечо силы.

Другими словами, момент относительно оси равен нулю, если сила и ось лежат в одной плоскости.

 

3. Напишите уравнения равновесия для произвольной пространственной систе­мы сил.

равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из трех координатных осей и суммы их моментов относительно этих осей были равны нулю.

∑ x_i =0, ∑ M_ix=0; ∑ y_{i =0}, ∑ M_iy=0; ∑ z_i =0, ∑ M_iz=0.

 

^ В результате изучения темы студент должен:

иметь представление о параллелепипеде сил, приведении пространственной системы сил к главному вектору и к главному моменту;

знать определение моментов относительно оси, условия равновесия пространственной системы сил.

Вопросы для самоконтроля

1. Что такое центр параллельных сил?

Центр параллельных сил есть точка, че­рез которую проходит линия равнодействую­щей системы параллельных сил, прило­женных в заданных точках, при любом изменении на­правления этих сил в простран­стве.

2. Как найти координаты центра параллельных сил?

Для определения координат центра параллельных сил воспользуемся теоремой Вариньона.

Относительно оси x

 

M_x(R) = Σ M_x(F_k), _-y_CR = Σ y_kFk и y_C = Σ y_kFk /Σ _Fk.

 

Относительно оси y

 

M_y(R) = Σ M_y(F_k), _-x_CR = Σ x_kFk и x_C = Σ x_kFk /Σ _Fk.

 

Чтобы определить координату z_C, повернем все силы на 90° так, чтобы они стали параллельны оси y (рисунок 1.5, б). Тогда

 

M_z(R) = Σ M_z(F_k), _-z_CR = Σ z_kFk и z_C = Σ z_kFk /Σ _Fk.

 

Следовательно, формула для определения радиус-вектора центра параллельных сил принимает вид

 

r_C = Σ r_kFk /Σ _Fk.

 

3. Что такое центр тяжести тела?

Центр Тяжести - неизменно связанная с твердым телом точка, через которую проходит равнодействующая сил тяжести, действующих на частицы этого тела при любом положении тела в пространстве. У однородного тела, имеющего центр симметрии (круг, шар, куб и т. д.), центр тяжести находится в центре симметрии тела. Положение центра тяжести твердого тела совпадает с положением его центра масс.

4. Как найти центр тяжести прямоугольника, треугольника, круга?

 

Для нахождения центра тяжести треугольника, необходимо нарисовать треугольник – фигуру, состоящую из трех отрезков, соединенных между собой в трех точках. Перед тем, как найти центр тяжести фигуры, необходимо, используя линейку, измерить длину одной стороны треугольника. В середине стороны поставьте отметку, после чего противоположную вершину и середину отрезка соедините линией, которая называется медианой. Тот же самый алгоритм повторите со второй стороной треугольника, а затем и с третьей. Результатом вашей работы станут три медианы, которые пересекаются в одной точке, которая будет являться центром тяжести треугольника. Если необходимо определить центр тяжести круглого диска однородной структуры, то для начала найдите точку пересечения диаметров круга. Она и будет центром тяжести данного тела. Рассматривая такие фигуры, как шар, обруч и однородный прямоугольный параллелепипед, можно с уверенностью сказать, что центр тяжести обруча будет находиться в центре фигуры, но вне ее точек, центр тяжести шара - геометрический центр сферы, и в последнем случае, центром тяжестью считается пересечение диагоналей прямоугольногопараллелепипеда.

5. Как найти координаты центра тяжести плоского составного сечения?

 

Метод разбиения: если плоскую фигуру можно разбить на конечное число таких частей, для каждой из которых положение центра тяжести известно, то координаты центра тяжести всей фигуры опредляются по формулам:

Х_C = ( s_k x_k ) / S; Y_C = ( s_k y_k ) / S,

где x_k, y_k - координаты центров тяжести частей фигуры;

s_k - их площади;

S = s_k - площадь всей фигуры.

 

 

6. Центр тяжести

 

 

1. В каком случае для определения центра тяжести достаточно определить одну координату расчетным путем?

В первом случае для определения центра тяжести достаточно определить одну координату Тело разбивается на конечное число частей, для каждой из которых положение центра тяжести C и площадь S известны. Например, проекцию тела на плоскость xOy (рисунок 1.) можно представить в виде двух плоских фигур с площадями S₁ и S₂ ( S = S₁ + S₂ ). Центры тяжести этих фигур находятся в точках C₁(x₁, y₁) и C₂(x₂, y₂). Тогда координаты центра тяжести тела равны

 

Так как центры фигур лежат на оси ординат (х = 0), то находим только координату Ус.

2 Как учитывается площадь отверстия в фигуре 4 в формуле для определения центра тяжести фигуры?

Метод отрицательных масс

Этот метод заключается в том, что тело, имеющее свободные полости, считают сплошным, а массу свободных полостей – отрицательной. Вид формул для определения координат центра тяжести тела при этом не меняется.

Таким образом, при определении центра тяжести тела, имеющего свободные полости, следует применять метод разбиения, но считать массу полостей отрицательной.

 

В результате изучения темы студент должен:

иметь представление о центре параллельных сил и его свойствах;

знать формулы для определения координат центра тяжести плоских фигур;

уметь определять координаты центра тяжести плоских фигур простых геометрических фигур и стандартных прокатных профилей.

ЭЛЕМЕНТЫ КИНЕМАТИКИ И ДИНАМИКИ
Изучив кинематику точки, обратите внимание на то, что прямолинейное движе­ние точки как неравномерное, так и равномерное всегда характеризуется наличием нормального (центростремительного) ускорения. При поступательном движении тела (характеризуемом движением любой его точки) применимы все формулы кинемати­ки точки. Формулы для определения угловых величин тела, вращающегося вокруг неподвижной оси, имеют полную смысловую аналогию с формулами для определе­ния соответствующих линейных величин поступательно движущегося тела.

Тема 1.7. Кинематика точки
При изучении темы обратите внимание на основные понятия кинематики: ускорение, скорость, путь, расстояние.

 

Вопросы для самоконтроля

1. В чем заключается относительность понятий покоя и движения?

 

Механическое движение -это изменение движения тела, или (его частей) в пространстве относительно др. тел с течением времени. Полет брошенного камня, вращение колеса- примеры механического движения.

2. Дайте определение основных понятий кинематики: траектории, расстоянию, пути, скорости, ускорению, времени.

 

Скорость – это кинематическая мера движения точки, характеризующая быстроту изменения ее положения в пространстве. Скорость является векторной величиной, т. е. она характеризуется не только модулем (скалярной составляющей), но и направлением в пространстве.

1234567Следующая ⇒

Поделиться:

Популярное:

1. II. Оценить степень развития мускулатуры, жира и костяка методом соматоскопии.
2. Больной 30 лет, страдающий сахарным диабетом I типа, обнаружен в коматозном состоянии через 3 часа после введения инсулина. Какое мероприятие необходимо выполнить в первую очередь?
3. Бомарше. Севильский цирюльник. Женитьба Фигаро.
4. Бхагаван, можете ли Вы объяснить, что такое «мужское эго» и что это означает, когда женщина использует это выражение по отношению к мужчине?
5. В условиях ОУ родители могут заполнить бланк заявления о согласии на проведение психологической работы с ребенком в ОУ в текущем учебном году.
6. Ваш диагноз? Какие дополнительные исследования необходимо выполнить? Какова тактика?
7. Во втором и третьем случаях, когда выбирается оптовый или розничный тип цен, следует заполнить еще несколько полей.
8. ГОЛОД ЗАСТАВИЛ ОЦЕНИТЬ СОЦИАЛЬНЫЕ СЛОИ НАРОДА
9. Граждане РФ могут исполнять воинский долг путем добровольного поступления на военную службу. Гражданам РФ предоставлено право заменить военную службу альтернативной гражданской службой.
10. Для оценки послеоперационной боли можно применить подход, представленный в таблице 2.2.
11. Для составления творческих рассказов от первого лица необходимо уточнить следующие знания