Магнитное взаимодействие проводников с токами. Контур с током в магнитном поле

Расчет силы Ампера, действующей на единицу длины двух параллельных проводников с токами I₁ и I₂ (рис. 2.9), дает величину:

,

где d - расстояние между проводниками.

Проводники с одинаково направленными токами I₁ и I₂ взаимно притягиваются, а проводники с противоположно направленными токами отталкиваются друг от друга.

Замкнутый проводящий контур с током произвольной геометри­ческой формы, помещённый в однородное магнитное поле, испытывает действие вращающего момента сил (рис. 2.10).

, М = р_m· В·sina,

где - магнитный момент контура с током, a - угол между магнитным моментом и магнитной индукцией.

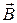Момент сил стремится установить магнитный момент по направлению магнитной индукции в положение устойчивого равновесия. Если внешние силы увеличивают угол a, то они совершают работу против сил магнитного поля и тем самым увеличивают энергию контура, которую можно вычислить следующим способом:

_внеш., .

Выражение, определяющее момент сил, действующий на контур с током в магнитном поле, дает еще один способ определения магнитной индукции.

Магнитная индукция численно равна вра­щающему моменту, действующему на небольшую рамку с током с единичным магнитным моментом, при такой его ориентации в поле, когда вращающий момент максимален. Направление вектора совпадает с вектором магнитного момента рамки, находящейся в положении устойчивого равновесия в рассматри­ваемой точке магнитного поля.

.

Если контур с током находится в неоднородном магнитном поле, то кроме вращающего момента сил на контур будет действовать результирующая сила, отличная от нуля, втягивающая контур в область сильного поля, когда угол между магнитным моментом и вектором индукции меньше p /2.

2.4. Циркуляция магнитного поля (закон полного тока) в вакууме. Теорема Гаусса для магнитного поля

 

Теорема о циркуляции для магнитного поля в вакууме

Циркуляция вектора магнитной индукции поля в вакууме равна алгебраической сумме токов, охватываемых этим контуром (т. е. результирующему току через поверхность, опирающуюся на контур L), умноженной на магнитную постоянную:

.

Силовые поля, для которых циркуляция силового вектора отлична от нуля, называются вихревыми или соленоидальными. Магнитное поле является вихревым, а его силовые линии (линии вектора ) - замкнуты.

Используя теорему о циркуляции, можно рассчитывать магнитные поля токов, обладающие определенной симметрией, например, индукции магнитных полей внутри тороида и бесконечно длинного соленоида.

Для соленоида: В = m₀·nI;

для тороида: ; R₂< r < R₁,

где n - число витков на единицу длины соленоида; N - полное число витков тороида; r - радиус окружности, лежащей внутри тороида; R₁ и R₂ - внутренний и наружный радиусы тороида.

Элементарным потоком магнитной индукции(магнитнымпотоком)сквозь малую поверхность площадью dS называется физическая величина, равная

.

Магнитный поток сквозь произвольную поверхность S (рис. 2.11)

 

.

Если магнитное поле однородное, а поверхность S плоская, то

 

Ф _m=В_n× S = B× S cos( ^ ).

 

Единица измерения магнитного потока в СИ - 1 Вб (вебер).

Теорема Гаусса для магнитного поля (силовые линии поля замкнуты)

 

Магнитный поток сквозь произвольную замкнутую поверхность равен нулю:

.

Работа перемещения проводника с током в постоянном магнитном поле

 

Элементарная работа, совершаемая силой Ампера при малом перемещении в магнитном поле элемента тока, рассчитывается следующим образом

 

.

 

При малом перемещении в магнитном поле проводника конечной длины с постоянным током I силы Ампера совершают работу

dA = I ·dФ _m,

где dФ _m - магнитный поток сквозь поверхность, которую описывает проводник при его малом перемещении.

Работа сил Ампера при перемещении в магнитном поле замкнутого контура с постоянным током I рассчитывается по формуле

A_1-2 = I DY = INDФ_m,

где DY – изменение потокосцепления контура при перемещении; N - количество витков контура; Ф_m - магнитный поток через поверхность контура. Все приведенные соотношения справедливы, если в проводниках поддерживается постоянная сила тока при любых перемещениях.

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Популярное:

1. XXIX. МЫ И ЭТОТ МИР – ПОЛЕВЫЕ СТРУКТУРЫ.
2. Анализ опасности поражения током в различных электрических сетях
3. Анализ результатов, полученных системой «Контур Стандарт»
4. Аналитическая платформа «Контур Стандарт» как инструмент реализации ROLAP-технологии: основные возможности, особенности и технология анализа информации
5. Атомно-молекулярное взаимодействие поверхностей. Оценка химического, молекулярного и электростатического взаимодействия и сопротивления движению.
6. БАШЕННЫЕ КОПРЫ ПРЕДПРИЯТИЙ ПО ДОБЫЧЕ ПОЛЕЗНЫХ ИСКОПАЕМЫХ
7. Бесполезное страдание и неверие
8. В 1990 году для участия в программе пилотируемых полётов представителей средств массовой информации был проведён отбор кандидатов в космонавты на конкурсной основе.
9. В зависимости от траектории полета мяча верхняя передача выполняется в средней или низкой стойках.
10. В неориентированном графе понятие дуга, путь, контур заменяются соответственно на ребро, цепь, цикл.
11. В общем анализе мочи: белок 14г/л, относительная плотность 1030, реакция щелочная, эритроциты до 20 в поле зрения, лейкоциты 8 в поле зрения гиалиновые цилиндры.
12. В экспериментальной и клинической нейрофизиологии с целью воздействия на функциональное состояние структур нервной системы применяют воздействие постоянным током.