
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Уравнение переноса. Вязкость газов
Интуитивные представления о вязкости жидкости каждый человек вырабатывает на основании повседневного опыта. Например, при использовании растительного масла, молока и других жидкостей. Вязкость или внутреннее трение, свойство жидкостей, характеризующее сопротивление действию внешних сил, вызывающих их течение. Вязкость проявляется в том, что при сдвиге соседних слоёв среды относительно друг друга возникает сила противодействия – напряжение сдвига. Прочувствовать это можно наблюдая за истечением воды или масла растительного. Рассмотрение предыдущих параграфов данной главы даёт основания утверждать, что такое свойство должно быть характерно и для газов. Это следует хотя бы из того, что газоподобные системы, представленные сами себе, в конце концов, переходят в устойчивое состояние теплового равновесия. Если при этом в газе имеются отдельные потоки, обладающие разной локальной скоростью относительно друг друга, то будет возникать препятствующая движению сила сопротивления. Первым этапом приближения к тепловому равновесию газа является обмен импульсом между «быстрыми» и «медленными» молекулами. Что это значит? В газовой среде в разных точках её пространства возможно движение отдельных струй газа, обладающих разной дрейфовой скоростью. Другими словами, в объёме пространства среды есть отдельные струи газа, движущиеся вдоль оси Х с некоторой локальной скоростью; будем обозначать её uх(z) и эта скорость «чувствительна» к положению в потоке. На рис. 7.7 представлены потоки слоёв с различной дрейфовой скоростью uх(z) как выше, так и ниже выделенной площадки D S. Не будем забывать, мы интересуемся только той частью переноса импульса, которая связана со столкновением молекул, но не с движением среды как целого. Итак, участвуя в перемещении элемента объёма газа как целого вдоль оси Х, молекулы газа участвуют и в хаотическом движении. Хаотические столкновения молекул (см. рис. 7.1) сопровождаются их перемещением из одного потока в другой, в результате чего дрейфовые скорости в двух соседних потоках постепенно уравниваются. Почему?
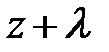 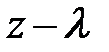 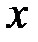 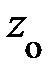 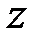 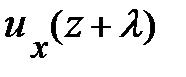 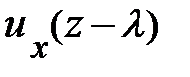 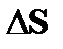 Вследствие обмена молекулами между струями (потоками), находящимися на расстоянии длины свободного пробега l выше и ниже слоя с координатой z = z0, происходит перенос импульса элемента объёма газа; молекулы «медленно» движущегося слоя проникают в «быстро» движущийся слой и наоборот; между молекулами происходит обмен импульсами. На опыте удобнее следить за дрейфовой (локальной) скоростью элемента объёма газа uх, следовательно, в уравнении (7.13) переносимой физической характеристикой j является импульс частицы, т.е. j º m× ui(z). Осознав переносимую физическую величину j в уравнении (7.13), перейдём к его преобразованию. Вследствие обмена молекулами между струями (потоками), находящимися на расстоянии длины свободного пробега l выше и ниже слоя с координатой z = z0, происходит перенос импульса элемента объёма газа; молекулы «медленно» движущегося слоя проникают в «быстро» движущийся слой и наоборот; между молекулами происходит обмен импульсами. На опыте удобнее следить за дрейфовой (локальной) скоростью элемента объёма газа uх, следовательно, в уравнении (7.13) переносимой физической характеристикой j является импульс частицы, т.е. j º m× ui(z). Осознав переносимую физическую величину j в уравнении (7.13), перейдём к его преобразованию.
Поскольку каждая молекула испытывает последнее столкновение на расстоянии длины свободного пробега l (рис. 7.7) импульс, переносимый через площадку D S за время Dt, запишется: D(N× j) º D(N× m× u(z)) = = D(N× рi); здесь m –, как догадался пытливый читатель, масса молекулы, а рi – её импульс в соответствующем слое. Суммарное изменение импульса запишется: Dр = D(N× рi). Каждый процесс переноса импульса связан с отклонением скорости частицы от её постоянного равновесного значения, т. е. определяется его темпом. И тогда в правой части уравнения (7.13) темп изменения импульса может быть представлен в виде: Dр = – Поскольку скорость u (7.5), длина свободного пробега l (7.10), m – масса молекулы газа являются характеристиками сортности газа, а n – концентрация частиц в единице объёма (7.8), то с учётом того, что m× n = = r – плотности газа, уравнение переноса импульса принимает вид: Dр = – Из второго закона Ньютона, формула (2.2), настойчивый читатель после преобразований приходит к формуле для силы вязкого трения вида: Fвяз. тр. = h× здесь h – коэффициент вязкости, равный h = Если переписать формулу (7.9) в виде:
Заменим отношение объёмов в выражении изменения энтропии на отношение чисел столкновений (с. 113)
Таким образом, явления переноса связаны с изменением энтропии. Вместе с тем, эти процессы могут быть не связаны с теплообменом между системой и окружающей средой и всегда ведут к увеличению энтропии. Из уравнения (7.19) также следует, увеличение энтропии может сопровождаться уменьшением числа столкновений между молекулами.
Реальные газы
8.1. Реальный газ малой плотности. В предыдущей главе и в работе [3, с. 52; 57] нам удалось достичь некоторого успеха в описании реальных газов малой плотности и при умеренных температурах. Это оказалось возможным благодаря тому, что неизвестный механизм взаимодействия молекул газа при столкновениях нам удалось обойти путём введения его неких средних характеристик (см. § 7.2). Однако с повышением давления и уменьшением температуры наблюдаются значительные отклонения от уравнения состояния идеального газа:
Естественно предположить, причины отступления свойств реальных газов от свойств идеального газа обусловлены простотой модели. В частности, отсутствием учёта собственных размеров молекул и тем, что характер сил взаимодействия между молекулами сложнее, чем для упругих шаров. Было бы неплохо предпринять усилия по уточнению влияния собственных размеров атомов (молекул) и механизма их взаимодействия на результаты исследований свойств реальных газов. Приступая к рассмотрению одноатомного газа из нейтральных атомов, ограничимся реальными газами малой плотности, когда расстояние между атомами достаточно велико. При таком подходе на эффективное расстояние взаимодействия rо (см. рис. 8.1) одновременно сближается не более двух атомов, что позволяет учитывать только парные взаимодействия и пренебречь взаимодействием трёх и более атомов одновременно. Почему? Во-первых, нами выбрана система, в составных частях (атомах) которой можно пренебречь внутренним движением и ограничиться только поступательным движением этих объектов. Кроме того, в такой системе возможен переход от фундаментальных кулоновских сил к нефундаментальным межатомным силам взаимодействия. При этом, как показывает эксперимент и теоретические расчёты физиков-теоретиков, характер зависимости энергии взаимодействия нейтральных атомов (молекул) U вз от r при малых расстояниях между ними, r ®0, подчиняется зависимости вида: U вз ~ r –n с n @ 12; т. е. может быть прописано как взаимодействие ионов. Причина здесь кроется в том, что характер сил отталкивания при r ®0 определяется ядрами атомов. Поэтому эти силы практически нечувствительны к тому, какие именно объекты сближаются – ионы или нейтральные атомы [2].
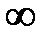 ) энергия взаимодействия между ними подчиняется зависимости вида: U вз ~ –r –mс m > 1, т.е. при больших расстояниях r между атомами могут возникать силы притяжения. Причиной здесь может выступать несимметричность в распределении зарядов в атоме или молекуле; типичным примером является молекула воды. В других атомах (молекулах) выбранной системы такое разделение зарядов может возникать под влиянием «соседей». В результате полной компенсации кулоновских сил взаимодействия не происходит, что и объясняет происхождение сил притяжения. ) энергия взаимодействия между ними подчиняется зависимости вида: U вз ~ –r –mс m > 1, т.е. при больших расстояниях r между атомами могут возникать силы притяжения. Причиной здесь может выступать несимметричность в распределении зарядов в атоме или молекуле; типичным примером является молекула воды. В других атомах (молекулах) выбранной системы такое разделение зарядов может возникать под влиянием «соседей». В результате полной компенсации кулоновских сил взаимодействия не происходит, что и объясняет происхождение сил притяжения.
Физики на опыте с инертными газами установили, что, несмотря на симметричность расположения электрических зарядов в них, полное выражение для энергии взаимодействия двух нейтральных атомов, справедливое при любом r, имеет вид:
Взаимодействие, энергия которого подчиняется зависимости вида (8.2), называется взаимодействием Ван-Дер-Ваальса. Во-вторых, межатомные силы взаимодействия приближённо удовлетворяют закону независимости действия сил, так что энергия взаимодействия в нашей системе атомов равна сумме энергий взаимодействия всех парных частиц и может быть представлена в виде: В-третьих, при r ® Оценим влияние взаимодействия атомов газа на его параметры в тепловом равновесии. Естественно ожидать, силы отталкивания препятствуют сближению двух атомов на бесконечно близкое расстояние. Это указывает на то, что эффективный объём газа Vэфф меньше объёма V занимаемого газом (Vэфф < V). Силы притяжения (рис. 8.1) должны влиять на давление реального газа; и прежде всего, влияние существования этих сил испытывают атомы вблизи стенки сосуда. Действительно, под воздействием этой силы, направленной внутрь газа, уменьшается концентрация атомов у стенки. В работе [3, с. 52] эту уменьшенную передачу импульса мы интерпретировали в среднем как давление газа. Под воздействием сил притяжения атомов их концентрация в пристеночном слое убывает. Согласно формуле Больцмана [3, с. 59] в «среднем поле», действующем на один атом газа, она изменяется по закону вида:
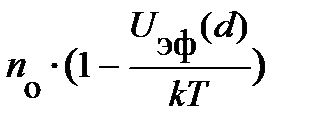 центрацию атомов внутри сосуда nо, т. е. центрацию атомов внутри сосуда nо, т. е. 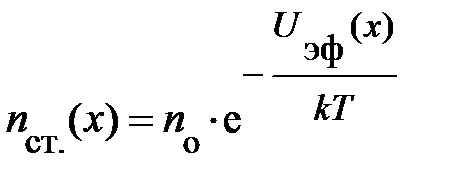 ; здесь введена более удобная координата х, перпендикулярная стенке сосуда и отсчитываемая от неё. Из рис. 8.2; 8.1 следует, что концентрация атомов у стенки nст.(х) отличается от nо только в слое от d до rо, при этом nст.(х) < < nо (рис. 8.2); т. е. концентрация в пристеночной области изменяется лишь в области эффективного взаимодействия d < х < rо. Кроме того, в формуле Больцмана требует уточнения понятие «среднего поля», обозначаемое символом ; здесь введена более удобная координата х, перпендикулярная стенке сосуда и отсчитываемая от неё. Из рис. 8.2; 8.1 следует, что концентрация атомов у стенки nст.(х) отличается от nо только в слое от d до rо, при этом nст.(х) < < nо (рис. 8.2); т. е. концентрация в пристеночной области изменяется лишь в области эффективного взаимодействия d < х < rо. Кроме того, в формуле Больцмана требует уточнения понятие «среднего поля», обозначаемое символом 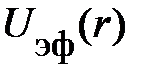 . .
Учёт только парных взаимодействий позволяет записать энергию взаимодействия N атомов в виде: p º pср.(d) = nо× k× T – nо× Второй член в этой формуле характеризует внутреннее давление, обусловленное притяжением атомов; в идеальном газе он отсутствует. Предпримем теперь усилия по осознанию смысла
где
Свяжем собственный объём атомов с размерами атома; представим, что атомы – твёрдые шарики. В таком приближении центры прочих атомов не могут попасть внутрь сферы, описанной вокруг центра выбранного шарика (желательно нарисовать образ). Радиус такой сферы «недоступности» равен диаметру атома,
Оценивая объём «недоступности» газа в целом, нужно умножить объём недоступности на число их пар N/2, чтобы не учесть дважды каждый атом. В результате объём «недоступности» газа из N атомов равен:
Разумеется, собственный объём атомов равен учетверённому объёму всех атомов лишь при малой плотности и становится непригодным с увеличением плотности газа. Таким образом, с учётом выражений (8.4) и (8.5) формула давления реального газа (8.3) принимает вид:
Пытливый читатель, проверяя операцию умножения, обнаружит, здесь опущен член, содержащий Uэф < < k× T в силу его малости, что оговаривалось в конце с. 117. Принято вводить обозначения: Итак, если число атомов N равно числу Авогадро NА, то уравнение Ван-дер-Ваальса для одного моля реального газа запишется:
Как следует изменить уравнение (8.7), чтобы оно сгодилось для любой массы газа? Настойчивый, а где-то и въедливый, читатель вспомнил понятие моля вещества и представил его на символическом языке: n = = N / NA = N× m0 / NA× m0 = m / M = r× V / r× Vo. Отсюда немедленно следует Vo = = V× M / m, а уравнение (8.7) принимает вид:
В заключение следует сказать, наводящие соображения, приведшие нас к уравнению Ван-дер-Ваальса, не являются его выводом.
8.2. Изотермы Ван-дер-Ваальса. Критическое
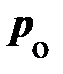 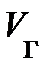 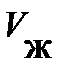 Чтобы выяснить смысл этой, странной на первый взгляд, зависимости, обратимся к опыту. Схема опыта следующая (рис. 8.4): в цилиндре А под поршнем В заключён один моль реального газа, температура которого поддерживается постоянной. Объём реального газа Vо может быть измерен по положению поршня В, а его давление – манометром С. На рис. 8.4, сверху, представлена экспериментально полученная изотерма при температуре ниже критической. Измерения показывают, при больших объёмах Vо с опусканием поршня В, объём реального газа уменьшается, а давление возрастает монотонно (рис. 8.4., участок изотермы 6®5); свойства реального газа аналогичны свойствам идеального газа. Чтобы выяснить смысл этой, странной на первый взгляд, зависимости, обратимся к опыту. Схема опыта следующая (рис. 8.4): в цилиндре А под поршнем В заключён один моль реального газа, температура которого поддерживается постоянной. Объём реального газа Vо может быть измерен по положению поршня В, а его давление – манометром С. На рис. 8.4, сверху, представлена экспериментально полученная изотерма при температуре ниже критической. Измерения показывают, при больших объёмах Vо с опусканием поршня В, объём реального газа уменьшается, а давление возрастает монотонно (рис. 8.4., участок изотермы 6®5); свойства реального газа аналогичны свойствам идеального газа.
При достижении некоторого определённого давления изотерма реального газа идёт не по кривой 5®4®3®2 (рис. 8.4), как этого требует уравнение (8.7), а по изобаре 5®2, т. е. в точке 5 свойства реального газа резко изменяются; происходит расслоение вещества на две фазы: жидкую и газообразную. При дальнейшем опускании поршня давление насыщенного пара pо, начиная с точки 5, остаётся постоянным; начинается процесс конденсации (ожижения) реального газа. Чем дальше опускается поршень, тем Таким образом, уравнение Ван-дер-Ваальса описывает не только газообразные состояния вещества, но охватывает и процесс перехода вещества в жидкость, и процесс её сжатия. В хорошем соответствии с результатами измерений уравнение Ван-дер-Ваальса показывает сближение точек 5®2, соответствующих объёмам Vг и Vж, по мере повышения температуры (рис. 8.4 и 8.3). Горизонтальный участок изотермы сокращается, стягиваясь в точку К. Температура, соответствующая изотерме с точкой К, а вместе с ней объём и давление (рис. 8.3) принято называть критическими – Tк, Pк, Vк. При Tк исчезает всякое различие между жидкостью и паром. Предпримем усилия по нахождению взаимосвязи между критическими параметрами состояния Tк, Pк, Vок для одного моля газа и постоянными а и b уравнения Ван-дер-Ваальса. Преобразуем уравнение Ван-дер-Ваальса:
раскрыв скобки (выполнили? ), умножив левую и правую части на Vо2/р (сделали? ) и собрав члены, содержащие Vо в одинаковых степенях, приходим к выражению вида:
Отсюда непосредственно следует, уравнение Ван-дер-Ваальса представляет собою уравнение третьей степени относительно Vо. Запишем его для критической температуры Tк:
Изотерма с температурой Tк, рис. 8.3, в точке К имеет перегиб, поэтому в этой точке уравнение (8.9) имеет тройной корень Vок и, как доказывается в алгебре, может быть представлено в виде:
если выполнить возведение в степень, то
Оба уравнения (8.9) и (8.9 а) тождественно совпадают между собой, если коэффициенты при одинаковых степенях Vо равны, т. е.:
Решая эти уравнения относительно трёх неизвестных, пытливый читатель, например, разделив последнее равенство на предпоследнее, получит:
где В заключение обратим внимание на то, что экспериментальная изотерма 2®5 (рис.8.4) имеет прямолинейный участок вместо завитка 5®4®3®2. Это объясняется неустойчивостью однородных состояний, отвечающих завитку 5®4®3®2.Если пытливый читатель возьмёт производную на участке 3®4 и, проявив терпение, запишет её через приращение, т. е. Dр/DV, то убедится, что она положительна(? ). Это означает – увеличение объёма сопровождается ростом давления, что, естественно, является противоестественным. На участках 2®3 и 3®4 Dр/DV отрицательна (убедились? ), эти участки могут быть реализованы. Однако в силу их неустойчивости (метастабильны) они требуют выполнения соответствующих условий, в частности, исключения посторонних примесей. Участок 5®4 соответствует пересыщенному пару, а 2®3 – перегретой жидкости. Свойства этих состояний нам потребуются в третьем семестре основного курса физики.
Популярное:
|
Последнее изменение этой страницы: 2017-03-11; Просмотров: 776; Нарушение авторского права страницы