
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
К вопросу о понятии кристалла
Понятие сплошной среды было введено и рассмотрено нами в работе [3, с. 35–37]. Характерной особенностью этих сред (твёрдых, жидких и газообразных) является то, что кроме большого числа частиц N ~ NA > > 1 они проявляют упругие свойства; способность восстанавливать свою форму, искажённую в результате кратковременного действия внешней силы. Эта способность среды является причиной того, что всякое механическое действие передаётся средой с конечной скоростью. Для простоты рассуждений в качестве сплошной среды будем рассматривать модель идеального кристалла (рис.6.1): точки равновесного расположения атомов образуют регулярный строй – структуру кристалла, её пространственную периодичность, неограниченную во всех трёх измерениях; она, структура, как бы состоит из бесконечно повторяющихся частей.
 В условиях равновесного состояния при (T > 0), которое сложилось в среде при отсутствии внешнего воздействия, частицы среды (атомы, ионы, молекулы) непрерывно колеблются около положений равновесия, причём интенсивность колебаний растёт с температурой. В условиях равновесного состояния при (T > 0), которое сложилось в среде при отсутствии внешнего воздействия, частицы среды (атомы, ионы, молекулы) непрерывно колеблются около положений равновесия, причём интенсивность колебаний растёт с температурой.
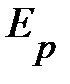 , рис. 6.2., имеет минимум в точке r = r0, то при нарушении равновесия будут возникать соответственно силы притяжения или отталкивания между атомами (ионами), что ведёт к возникновению упругой деформации в среде. При малых деформациях вблизи точки равновесия, х < < r0, потенциальная энергия с достаточной степенью точности может быть представлена аналитическим выражением , рис. 6.2., имеет минимум в точке r = r0, то при нарушении равновесия будут возникать соответственно силы притяжения или отталкивания между атомами (ионами), что ведёт к возникновению упругой деформации в среде. При малых деформациях вблизи точки равновесия, х < < r0, потенциальная энергия с достаточной степенью точности может быть представлена аналитическим выражением 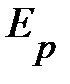 = Е(r0) + kx2/2. Поскольку сила является первой производной от потенциальной энергии, с. 30 формула (2.5), естественно ожидать, частица (атом) совершает малые гармонические колебания около состояния равновесия (T > 0). Колебания частиц в сплошной среде не являются независимыми. Сместившаяся из положения равновесия частица увлекает с собой ближайшие к ней частицы. Сильное взаимодействие между частицами среды приводит к тому, что возмущение, вызванное колебанием какой-либо частицы, передаётся другим частицам. Отсюда немедленно следует, упругая деформация может распространяться в сплошной среде. Распространение колебаний в среде, в нашем случае упругой деформации, называется бегущей волной. Бегущая упругая волна, достигнув границы сплошной среды (кристалла), может отражаться. При наложении прямой и отражённой волн возникают так называемые стоячие волны. Естественно, они должны отвечать соответствующим условиям. В частности, в среде возникают стоячие волны с набором дискретных частот, половина длины волны которых укладывается в сплошной среде целое число раз. Аналитически это может быть записано как L = n× = Е(r0) + kx2/2. Поскольку сила является первой производной от потенциальной энергии, с. 30 формула (2.5), естественно ожидать, частица (атом) совершает малые гармонические колебания около состояния равновесия (T > 0). Колебания частиц в сплошной среде не являются независимыми. Сместившаяся из положения равновесия частица увлекает с собой ближайшие к ней частицы. Сильное взаимодействие между частицами среды приводит к тому, что возмущение, вызванное колебанием какой-либо частицы, передаётся другим частицам. Отсюда немедленно следует, упругая деформация может распространяться в сплошной среде. Распространение колебаний в среде, в нашем случае упругой деформации, называется бегущей волной. Бегущая упругая волна, достигнув границы сплошной среды (кристалла), может отражаться. При наложении прямой и отражённой волн возникают так называемые стоячие волны. Естественно, они должны отвечать соответствующим условиям. В частности, в среде возникают стоячие волны с набором дискретных частот, половина длины волны которых укладывается в сплошной среде целое число раз. Аналитически это может быть записано как L = n×  . Здесь под L подразумевается линейный параметр сплошной среды, например, кристалла (в трёх направлениях), представленного на рис. 6.1, а ln = . Здесь под L подразумевается линейный параметр сплошной среды, например, кристалла (в трёх направлениях), представленного на рис. 6.1, а ln =  – наименьшее расстояние между двумя точками, осуществляющими колебания в одной фазе (длина волны). Таким образом, в тепловом равновесии кристалл (твёрдое тело) может быть представлен набором (спектром) дискретных частот (стоячих волн). – наименьшее расстояние между двумя точками, осуществляющими колебания в одной фазе (длина волны). Таким образом, в тепловом равновесии кристалл (твёрдое тело) может быть представлен набором (спектром) дискретных частот (стоячих волн).Итак, при T > 0 проявляются динамические нарушения структуры кристалла. Тем не менее, взаимная упорядоченность в расположении частиц в ней, т. е. их регулярный строй, сохраняются (рис. 6.1). Это обстоятельство (сохранение регулярного строя) и интенсивное взаимодействие частиц, Из гипотезы о равномерном распределении энергии по степеням свободы следует, что средняя кинетическая и средняя потенциальная энергии в тепловом равновесии равны Особенностью этих «квазичастиц» является отсутствие поступательных степеней свободы. Частоты их колебаний могут быть любыми и никак не связаны с частотами спектра «коллективных квазичастиц». Иными словами, в области умеренных температур кристалл, по существу, можно моделировать системой «невзаимодействующих» атомов, совершающих независимые колебания. Никакого противоречия здесь нет. «Индивидуальные квазичастицы», которым мы придали ряд признаков исходных частиц, это всё же квазичастицы (квазиатомы). Их отличие в том, что они не обладают поступательным движением и удерживаются в узлах кристалла благодаря взаимодействию, обеспечивающему само его, кристалла, существование. Таким образом, качественное рассмотрение кристалла в модели «квазичастицы» позволило сформировать представление о кристалле. В частности, в состоянии теплового равновесия в области умеренных температур кристалл может быть представлен как возможное множество частот собственных колебаний или стоячих волн. Иными словами частотный спектр (моды колебаний) – это внутренняя характеристика кристалла. В существовании множества частот (мод) колебаний можно убедиться из примера, представленного на рис. 6.3. Он позволяет убедиться в том, что возможное множество мод колебаний определяется числом степеней свободы каждого элемента системы. В системе из двух элементов (атомов) существуют две моды колебаний (рис. 6.3), тогда как система из трёх атомов обладает тремя степенями свободы, т.е. возможны три стоячих волны. Естественно ожидать, в системе из N элементов (атомов) существует N мод колебаний.
6.2. Понятие волны. Уравнение плоской волны. В предыдущем семестре нам удалось уяснить причину возникновения волнового движения [3, с. 36 со второго абзаца, с. 37, 38 со второго абзаца] – упругая деформация в сплошных средах передаётся последовательно от одной точки среды к другой. Рассмотрение упругих колебаний в кристалле, параграф 6.1, оказалось успешным, потому что мы могли трактовать тепловые возбуждения в нём как газоподобную систему, состоящую из независимых частицеподобных объектов. Успех был связан с тем, что мы можем мысленно расчленять макроскопический объект на физически малые элементы объёма. При этом элемент сплошной среды может играть роль «частицы», за взаимодействием и движением которой мы в состоянии наблюдать на опыте. Поэтому подход к рассмотрению обозначенных в данном параграфе вопросов в модели «размазанного» по некоему объёму вещества неизбежен. Простейшим движением в сплошных средах является распространение упругой деформации, возникающей под действием внешней силы. Действительно, возникшие при деформации упругие силы стремятся вернуть элементы среды к первоначальному состоянию равновесия; благодаря взаимодействию между соседними элементами среды упругие деформации будут передаваться от одних участков среды к другим, более удалённым от начального возбуждения. Очевидно, что это движение устанавливается не сразу и внешняя сила должна действовать периодически, например, по закону F = Fo× sinwt. Распространяющиеся по кристаллу (сплошной среде) вынужденные колебания называются бегущей упругой волной в противоположность стоячей упругой волне. В зависимости от характера возникающих при этом деформаций различают продольные волны (в жидкостях, газах и твёрдых телах) – частицы среды колеблются вдоль линий распространения колебаний и поперечные (в твёрдых телах? )
   – частицы среды колеблются перпендикулярно направлению распространения волны (рис. 6.4.). Бегущая волна отличается от стоячей. В частности, фаза колебаний двух разных элементов (квазичастиц) сплошной среды, по которой распространяется бегущая гармоническая волна, не совпадает с фазой этих же элементов в стоячей волне, отвечающей той же самой частоте (моде) колебаний. В стоячей волне все частицы, участвующие в данной моде (колебании), осуществляют колебания, обладая одной и той же фазой. В бегущей же волне всё обстоит иначе. Если колеблющийся элемент находится дальше от края, к которому приложена вынуждающая сила (рис. 6.4), то он будет совершать абсолютно такое же движение, что и ближайшие частицы, но в более поздний момент времени Dt. Этот промежуток времени необходим для того, чтобы возбуждение (бегущая волна) прошло это расстояние. Найдём связь между состояниями колебательного движения в различных точках среды. Будем искать закон движения бегущей волны в виде: yбег (х, t) = = yo× sinj (х, t), где величина j (х, t) = w t – d× х называется фазой бегущей гармонической волны. Неизвестную d-дельта определим из условия совпадения фаз колебаний частиц среды j х = j х +Dх в точке х и в точке х +Dх (рис. 6.4), до которой распространится возбуждение (уплотнение) к моменту времени t +Dt. Тогда, сравнивая аргументы функций yбег(х, t) и yбег(х +Dх, t +Dt), приходим к равенству: j (х, t) = (w t – d х) = j (х +Dх, t +Dt) = w (t +Dt) – d× (х +Dх). (6.1) Поскольку j х = j х +Dх, разность фаз должна равняться нулю: Dj = j х +Dх – j х = 0 и пытливый студент, проделав преобразования, из равенства (6.1) приходит к выражению вида: [w (t +Dt) – d× (х +Dх)] – (w t – d х) = 0, откуда немедленно следует, неизвестная величина d-дельта равна:
Здесь С учётом (6.2) закон движения бегущей волны примет вид: yбег (х, t) = yo× sin(w t – Обсудим некоторые свойства бегущей волны. Нетрудно видеть, и это следует из уравнения (6.3), что при t = const убег (х) является периодической функцией х. Действительно, если учесть, что циклическая частота w = 2p/T, уравнение волны приобретает вид: убег (х) = yo× sin( здесь t = 0; знак «–» можно опустить, поскольку здесь он лишь подчёркивает запаздывание колебаний в удалённых точках сплошной среды. Из вида представленного уравнения следует, период этой синусоиды в пространстве равен произведению u× Т = l. Этот пространственный период, т. е. расстояние, через которое повторяется волнообразное распределение в среде (рис. 6.5), носит название длины волны. С ним мы познакомились в работе [3, с. 39]. Таким образом, мы получили известное соотношение, связывающее скорость движения волны с длиной волны и периодом колебания точки. При х = const уравнение волны приобретает вид: убег (t) = yo× sinw t, и, являясь периодической функцией t, отражает колебательный процесс частиц в данной точке среды. Здесь уместно заметить, при волновой передаче деформации через среду по закону синуса меняется ряд физических величин: смеще
  ние точки от положения равновесия, скорость колеблющихся частиц, давление, плотность. Поэтому уравнение волны, которым мы оперируем, является весьма общим. Под символом функции у может быть любая из перечисленных физических величин, изменяющихся по закону синуса при движении волны вдоль направления х. Правда, не все физические величины обязаны быть в одной фазе. ние точки от положения равновесия, скорость колеблющихся частиц, давление, плотность. Поэтому уравнение волны, которым мы оперируем, является весьма общим. Под символом функции у может быть любая из перечисленных физических величин, изменяющихся по закону синуса при движении волны вдоль направления х. Правда, не все физические величины обязаны быть в одной фазе.
В формуле бегущей волны (6.3) колеблющаяся величина зависит от двух изменяющихся параметров: положения в пространстве среды х и времени t. Найдём частные производные от функции yбег (х, t) по времени при постоянном х:
Если у – смещение частиц среды при колебаниях, то u и а будут скоростью и ускорением этих частиц при их колебательном движении в точке с координатой х, т. е. Из уравнений (6.4) следует связь между амплитудными значениями этих величин: u0 = y0× w, a0 = y0× w2 = u0× w. Частные производные от функции yбег (х, t) по х при t = const запишутся:
Поскольку y есть смещение частиц среды при колебаниях, то производная по х, при постоянном t, показывает изменение значения колеблющейся величины у на единицу расстояния между точками среды Dх = х2 – – х1. Другими словами, как увеличивается или уменьшается у вдоль оси х в данный момент времени. Пытливый читатель может на рисунке, подобном (рис. 6.5), выбрать две точки на оси х и увидеть, как изменяется смещение y частицы при колебаниях на расстоянии Dх. В заключение параграфа следует обратить внимание на частные производные второго порядка, уравнения (6.4 б) и (6.5 б). Из уравнений следует, изменения в движении квазичастицы в данной точке среды (6.4 б) могут быть связаны с изменениями в движении квазичастицы, обусловленными её пространственным расположением (6.5 б). Действительно, если в правую часть уравнения (6.5 б) подставить левую часть уравнения (6.4 б), немедленно приходим к уравнению, связывающему быстроту изменения в движении квазичастицы, обусловленную её пространственным движением, с быстротой изменения в движении частицы, связанную со временем:
Это дифференциальное уравнение плоской гармонической волны, распространяющейся по оси Х, называется волновым уравнением. Несмотря на то, что волновое уравнение получено нами из уравнения волны (6.3), можно сделать и обратное заключение – если физическая величина у = у (х, t) зависит от времени и координат так, что её частные производные удовлетворяют уравнению (6.6), то величина у распространяется в среде в виде плоской волны. И ещё один факт следует отметить, уравнение (6.5 б) не содержит времени и с учётом того, что w = 2p/T, а u = l/Т принимает вид:
Итак, на первый взгляд нам удалось найти наиболее пригодную физическую модель для описания движения в континуальной физике – это бегущая волна вида: Из наших рассуждений следует, особенностью элементов сплошной среды как «частиц» является то, что они могут двигаться независимо. Любое их движение должно быть таким, чтобы не разрушить целостность среды. Нам удалось в этом убедиться на уровне общих слов в работе [3, с. 44, 45]. Чтобы найти подтверждение качественному своеобразию упругих волн, следует обратиться к вопросу об энергии бегущих упругих волн.
6.3. Плотность энергии в бегущей В предыдущих параграфах данной главы мы убедились в том, что малые деформации элемента сплошной среды приводят к возникновению упругих волн. Упругие волны в сплошной среде – это согласованное «коллективное» движение системы «частиц» – элементов среды. Каждый элемент среды испытывает смещение u(х, t), определяемое местом его расположения (пространственная форма волны) и временем. Изменения величины u(х, t) и связанных с ней физических характеристик распространяются с течением времени с фазовой скоростью uф. Чтобы убедиться в качественном своеобразии упругих волн как «коллективном» типе движения системы частиц, рассмотрим вопрос об энергии бегущих упругих волн. Наблюдаемое сходство упругих волн в разных сплошных средах позволяет, для простоты рассуждений, обратиться к продольным упругим волнам. При этом мы можем ссылаться на упругие волны в цепочке атомов и в сплошном твёрдом теле (раздел 6.1). Вспомним, внутренняя энергия цепочки атомов при тепловом движении может быть представлена как сумма кинетической и потенциальной энергий (энергия, не зависящая от температуры, не учитывалась) вида:
здесь К / i – кинетическая энергия i-того элемента цепочки,
 = = 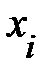 + ui (t), где + ui (t), где  – положение i-го элемента среды в состоянии равновесия, а ui (t) – смещение, вызванное упругой деформацией, распространяющейся в среде (рис. 6.6). В этом пытливый читатель так же может убедиться, обратившись к рис. 6.2. – положение i-го элемента среды в состоянии равновесия, а ui (t) – смещение, вызванное упругой деформацией, распространяющейся в среде (рис. 6.6). В этом пытливый читатель так же может убедиться, обратившись к рис. 6.2.
И тогда кинетическая энергия i – того элемента среды
убедиться в справедливости аналитической записи можно через рис. 6.6. Потенциальная энергия взаимодействия, с. 81, запишется:
где В итоге, внутренняя энергия цепочки элементов сплошной среды может быть выражена только через смещение элементов среды. Действительно, внутренняя энергия i-го элемента (атома)
В непрерывном приближении для цепочки элементов среды длиной DL, содержащей DN атомов (элементов), расстояние между которыми a, а длина цепочки DL = DN× a, внутренняя энергия DE содержит DN одинаковых слагаемых (6.10). Тогда для внутренней энергии этого элемента цепочки из DN атомов, заменив операцию суммирования в (6.8) умножением, получим
Заменим теперь через плотность rо и объём DV массу DМ = DN× m = = rо× DV, а коэффициент упругости k через модуль Юнга c–хи, k = = c× DS/а. Пытливый читатель в этом может убедиться, если обратится к рис. 6.6 и воспользуется законом Гука. (F = k × Du, F = c× DS× e, e = Du/а; здесь a – расстояние между ближайшими атомами среды (упругие свойства не зависят от длины образца); Du – деформация между ближайшими атомами, возникшая в результате внешнего воздействия, и < < а; DS – площадь поперечного сечения цепочки атомов, e – относительное увеличение расстояния между ближайшими атомами.) Теперь уточним разность смещений между двумя соседними атомами. Если воспользоваться разложением функции в ряд Тейлора, то Убедимся в правоте утверждения из рассуждений. Пусть смещение частицы I сплошной среды между точками 1-3 (рис. 6.6) отражается функцией u(t, х), а между частицами 2-4 функцией u(t, х+Duj(t, x)); здесь Duj(t, x) – смещение j-го атома в результате распространения упругой деформации. Смещение частицы под номером 3 в состояние 4 запишется: Duj(t, x)=Dui+u(t, x+Duj(t, x))–u(t, х); здесь Dui – смещение i-того атома из состояния 1 в 2. Тогда изменение Dux=Duj–Dui запишется: Dux=u(t, х+Duj)–u(t, х). Теперь вспомним, частная производная от функции u / (t, х) = = Введённые физические характеристики среды и характеристики смещения её частиц при возникновении упругой деформации позволяют преобразовать уравнение (6.11) для внутренней энергии элемента цепочки из DN атомов длины DL = DN× a к виду:
здесь DV = DSх× (DN× а) = DSх× DL, где DL – длина элемента цепочки. Величина
называется плотностью внутренней энергии цепочки атомов в приближении сплошной среды; где rкин – плотность кинетической энергии, а rвзаим. –плотность энергии взаимодействия. Теперь вспомним, для бегущей вдоль оси х упругой волны справедливо соотношение:
В этом пытливый читатель может убедиться, если найдёт первую производную от функции упругой деформации Из уравнений (6.12) и (6.13) следует
Иначе говоря, в любой момент времени и в любой точке пространства плотность кинетической энергии в сплошной среде равна плотности энергии взаимодействия. Отсюда следует, плотность энергии в упругой волне равна:
При прохождении бегущей упругой волны вдоль оси х происходит распространение энергии. Процесс переноса энергии характеризуется вектором плотности потока энергии jx, модуль которого равен количеству энергии переносимой в единицу времени через единичную (например, 1 м2) поперечную площадку. Таким образом, упорядоченный перенос энергии jx вдоль оси х должен иметь форму произведения плотности энергии Чтобы записать это произведение, уточним механизм упорядоченного переноса энергии в сплошной среде. Из работы [2] следует, в сплошной среде возможны два механизма упорядоченного переноса энергии через какую-либо поверхность. Одним из них является перенос плотности энергии вида (6.12) со скоростью смещения Однако возможен упорядоченный перенос энергии и через поверхность DSх, окружающую элемент среды объёмом DV. Действительно, на границе объёма возникают упругие напряжения (рис. 6.7):
Учтём теперь то, что мы рассматриваем лишь малые смещения элемента сплошного твёрдого тела. Тогда из (6.15)
определяется лишь вкладом работы упругих поверхностных сил. Это приближённое выражение может быть представлено в другом виде, если учесть (6.13) и (6.14), из которого следует, что
Другими словами, в указанном приближении упругая волна описывает перенос плотности механической энергии, либо перенос плотности внутренней энергии также в направлении оси х, но при этом re < < Dre. Выражение (6.18) для потока механической энергии в бегущей волне справедливо и для поперечных упругих волн в твёрдом теле и для упругих волн в жидкости. Убедиться в этом можно в работе [2, глава 4]. В заключение параграфа заметим. Упругие волны – это такой тип «коллективного» движения сплошной среды и, следовательно, такой способ распространения энергии в пространстве и во времени, при котором с фазовой скоростью внутренняя энергия может переноситься на любые расстояния практически без переноса массы. При этом энергия покоя, равная произведению плотности массы на скорость света в квадрате, много больше плотности энергии Таким образом, бегущая упругая волна как самостоятельный тип движения сплошной среды принципиально отличается от способа переноса энергии при движении одиночной частицы, когда одновременно переносится как масса частицы, так и вся связанная с ней энергия. По сути, вместо детального рассмотрения движения элемента сплошной среды объёма Нормальную моду (распространяющееся колебание) с гармонической зависимостью от времени как простейший вариант модели бегущей волны, можно сопоставить с частицей, движущейся в стационарном состоянии как простейшим вариантом модели частицы. У частицы в этом случае сохраняется механическая энергия Емех = const, тогда как у бегущей нормальной моды гармонического типа сохраняется средний поток механической энергии
Популярное:
|
Последнее изменение этой страницы: 2017-03-11; Просмотров: 644; Нарушение авторского права страницы