
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Электрическое поле системы проводников⇐ ПредыдущаяСтр 23 из 23
До сих пор мы отвлекались от вопроса о том, каким образом можно было бы реализовать систему неподвижных зарядов. И здесь так же полезно обратиться к суждениям А.Д. Суханова [2].
Ответ на обозначенный вопрос не прост хотя бы потому, что свободные одноимённые заряды отталкиваются и всегда стремятся удалиться друг от друга на бесконечные расстояния. Что касается системы свободных разноимённых зарядов, то хотя и нетрудно представить случай, когда результирующие силы, действующие на любой заряд, обращаются в нуль (рис. 9.9.), равновесие в такой системе неустойчиво. Единственная возможность исследовать электрические свойства такой системы – это допустить, что на неё одновременно действуют силы неэлектрической природы, которые совместно с кулоновскими силами обеспечивают её устойчивость, не влияя на электрические свойства системы. На опыте система неподвижных зарядов осуществляется, например, в проводниках. Для простоты будем иметь в виду металлические проводники, состоящие из положительно заряженных ионов, образующих кристаллическую решётку, и коллективизированных электронов, не принадлежащих отдельным атомам. Суммарные заряды решётки Q + и системы электронов Q – очень велики, но в нормальных условиях точно компенсируют друг друга | Q + | = | Q – | = Q, так что в целом проводник электронейтрален. Ионы массивны и сильно связаны друг с другом, в первом приближении их можно считать неподвижными. Электроны же подвижны и внутри проводника могут приближённо считаться свободными. Малейшее воздействие внешнего поля приводит их в движение, что означает появление электрического тока. Проводники обладают способностью приобретать или терять, без разрушения проводника, некоторое число электронов, приносящее или уносящее заряд DQ; электризация проводника. Если электроны проводника теряются, он оказывается заряженным положительно, если приобретаются – отрицательно, причём модуль заряда проводника |DQ| < < Q. Таким образом, изменение заряда проводника при электризации составляет ничтожную долю от суммарного заряда ионов решётки. Очевидно, при наличии только электрических сил подвижные электроны могли бы покинуть проводник. Этого не происходит потому, что на них действуют силы неэлектрической природы, препятствующие вылету электронов из проводника. Можно считать, что электроны находятся в некоей потенциальной яме, покинуть которую они могут лишь получив дополнительную энергию, называемую работой выхода Авых.. Очевидно, исключив другие воздействия и ограничившись рассмотрением не слишком сильных постоянных электрических полей, металлические проводники – это материальные объекты, позволяющие реализовать на опыте системы неподвижных зарядов. Для дальнейшего нам достаточно знать некоторые важнейшие свойства проводников, подтверждаемые многочисленными экспериментальными данными. Во-первых, избыточный заряд любого знака всегда скапливается у поверхности проводника. Почему? Внутри проводника электроны свободны и движутся, взаимно отталкиваясь, до тех пор, пока не разместятся на наиболее далёких друг от друга расстояниях. Тем самым, в состоянии равновесия объёмная плотность заряда проводника устанавливается равной нулю rq = 0 (рис. 9.10), так что проводники играют роль материальных объектов, позволяющих осуществить поверхностное или линейное распределение зарядов (см. 9.16). Во-вторых, электрическое поле системы неподвижных зарядов внутри проводника всегда равно нулю: Евнутр. = 0 (рис. 9.10). Если это было бы не так, то под действием отличного от нуля электрического поля свободные электроны пришли бы в движение и двигались бы до тех пор, пока перераспределение зарядов не обеспечило выполнение этого условия. Соответственно, электрический потенциал внутри проводника постоянен: jвнутр. = const.
Указанные выше свойства проводников во многом упрощают расчёт соответствующих полей. Перейдём к рассмотрению простейших примеров расчёта, когда размерами проводников по двум или одному направлениям можно пренебречь. Пример 1. Найти поле бесконечно длинной прямой нити с линейной плотностью заряда t = const. Какой потенциал соответствует этой поверхности?
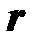  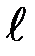 Решение: Возьмём длинную прямую нить, несущую положительный электрический заряд с линейной плотностью t. Чтобы воспользоваться законом Гаусса, охватим нить с зарядами поверхностью в виде цилиндра некоторого радиуса r коаксиального заряженной нити и имеющего длину Решение: Возьмём длинную прямую нить, несущую положительный электрический заряд с линейной плотностью t. Чтобы воспользоваться законом Гаусса, охватим нить с зарядами поверхностью в виде цилиндра некоторого радиуса r коаксиального заряженной нити и имеющего длину 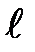 (рис. 9.11). На такой поверхности по соображениям симметрии Е = Еn = const. На основании цилиндра Еn = 0. Поэтому по закону Гаусса NЕ = Sбок× Еn = 4× p× k× q. Если учесть, что заряд нити q = t× (рис. 9.11). На такой поверхности по соображениям симметрии Е = Еn = const. На основании цилиндра Еn = 0. Поэтому по закону Гаусса NЕ = Sбок× Еn = 4× p× k× q. Если учесть, что заряд нити q = t× 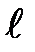 , то NЕ = 4× p× k× t× , то NЕ = 4× p× k× t× 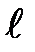 = = Еn× 2p× r × = = Еn× 2p× r × 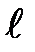 . Здесь 2p× r . Здесь 2p× r 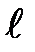 – площадь боковой поверхности цилиндра, коаксиального (имеющего общую ось с) заряженной нити. Из последнего равенства следует, что Еn = – площадь боковой поверхности цилиндра, коаксиального (имеющего общую ось с) заряженной нити. Из последнего равенства следует, что Еn = 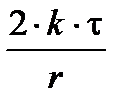 , модуль электрического поля убывает как 1/r. Здесь, равно как и ранее, k = 1/(4× p× eо). , модуль электрического поля убывает как 1/r. Здесь, равно как и ранее, k = 1/(4× p× eо).
Для нахождения потенциала электрического поля, создаваемого заряженной нитью, на поверхности коаксиального цилиндра радиуса r воспользуемся уравнением взаимосвязи силового поля с энергетическим (9.7):
Библиографический список Основной список 1. Бондарев, Б.В. Курс общей физики. В 3 кн. Кн. 1. Механика: учеб. пособие / Б.В. Бондарев, Н.П. Калашников, Г.Г. Спирин. – 2-е изд. – Москва: Высш. шк., 2005. – 352 с. 2. Суханов, А.Д. Фундаментальный курс физики: учеб. пособие для вузов. В 4-х т. Т. 2. Континуальная физика / А.Д. Суханов. – Москва: Агар, 1998. – 709 с. 3. Лебедев, Я.Д. Пропедевтический курс по физике: учебное пособие / Я.Д. Лебедев. – Вологда: ВоГУ, 2014. – 86 с. 4. Редькин, Ю.Н. Курс общей физики / Ю.Н. Редькин. – Киров: ВятГГУ, 2009. – 603 с. Вспомогательный список 5. Геворкян, Р.Г. Курс физики: учеб. пособие / Р.Г. Геворкян. – Москва: Высшая школа, 1979. – 656 с. 6. Китайгородский, А.И. Введение в физику / А.И. Китайгородский. – Москва: Наука, 1973. – 688 с. 7. Минасян, Л.А. Единая теория поля: Философский анализ современных проблем физики элементарных частиц и космологии. Опыт синергетического осмысления / Л.А. Минасян. – Москва: КомКнига, 2005. – 176 с. 8. Савельев, И.В. Курс общей физики: Т.1: Механика, колебания и волны, молекулярная физика / И.В. Савельев. – Москва: Наука, 1973. – 511 с. 9. Савельев, И.В. Курс общей физики: Т.2: Электричество / И.В. Савельев. – Москва: Наука, 1973. – 431 с.
Учебное издание
Яков Дмитриевич Лебедев ФИЗИКА Часть 1 Популярное:
|
Последнее изменение этой страницы: 2017-03-11; Просмотров: 568; Нарушение авторского права страницы