
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Понятие об электрическом поле
В предыдущих главах мы убедились в том, что энергия и сила взаимодействия между частицами должны обладать довольно простыми свойствами. Поэтому в наших описаниях проблема сводилась к нахождению и поиску конкретных выражений энергии взаимодействия В предыдущих главах нам приходилось рассматривать либо выделенную заряженную частицу, например, формула (8.2), либо систему взаимодействующих зарядов (неподвижных или движущихся в малой области), каждый из которых (заряд) был равноправен. Предпримем усилия, чтобы объединить оба подхода и научиться выражать заданные внешние условия хотя бы для простейших ситуаций через характеристики системы заряженных частиц. А пока уточним понятие электрического заряда. Проявления фундаментального электромагнитного взаимодействия, с которыми человек встречается в повседневной жизни, менее наглядны, чем фундаментальные гравитационные силы. Это постоянные магниты, электризация в результате трения, молния, свет и т. п.. В основе этих явлений лежит и фундаментальная электрическая сила взаимодействия двух равноправно движущихся и взаимодействующих частиц любых зарядов qi и определяемая их мгновенным положением ri :
где r12 – мгновенное расстояние между заряженными частицами. С этой фундаментальной электрической силой Кулона читатель знаком ещё со школы и может убедиться в том, что она обладает всеми качествами силы взаимодействия. Входящие в неё скалярные параметры qi характеризуют присущую некоторым телам способность к «электрическому» взаимодействию. Их принято называть электрическими зарядами, или просто зарядами. В системе СИ постоянная k = 1/(4× p× eо), а eо = 8, 85× 10–12 Кл2/Н× м2; однако заметим, закон (9.1) справедлив только для неподвижных зарядов. Не менее важно: если зависимость (9.1) верна, то до каких малых или больших расстояний это имеет место? Прямые и косвенные измерения показывают, закон Кулона описывает взаимодействие неподвижных зарядов от 105 до 10–14 м. При очень малых расстояниях, понятие силы теряет смысл, но удаётся подтвердить справедливость соответствующего выражения для энергии взаимодействия; см, например, описание (8.2). Каковы же свойства новой фундаментальной величины – электрического заряда? Из наблюдаемой на опыте способности макроскопических тел относительно просто терять и приобретать заряд путём трения следует, какие-то носители заряда в веществе обладают очень малой массой и весьма подвижны. Экспериментально установлено, такими сверхлёгкими носителями заряда являются электроны. Масса электрона me = 9, 1× 10–31 кг и составляет ~ 1/2000 массы протона, а заряд его e = 1, 6× 10–19 Кл. Эту величину принято называть элементарным зарядом, и она представляет собой наименьший возможный заряд, существующий в природе. Любые другие заряды являются лишь целыми кратными е. Свойство «квантованности» электрического заряда логического объяснения пока не нашло. Зная величину и массу элементарного заряда, можно сравнить интенсивность электромагнитного и гравитационного взаимодействий, воспользовавшись формулой (9.1) и законом всемирного тяготения [3, с. 18]. Проделав вычисления, пытливый читатель увидит, что сила Кулона в 1042 раз больше силы тяготения, т. е. последняя фантастически мала. Встречающиеся на опыте заряды делятся на два типа, условно называемые положительными и отрицательными; принято считать заряд протона положительным qp = +|e|, а электрона qe = –|e| отрицательным. Из экспериментов следует, что заряды любого типа подчиняются одному и тому же закону Кулона. Тем не менее, одноимённые заряды отталкиваются, а разноимённые – притягиваются. Следует подчеркнуть, из определения заряда по (9.1) следует аддитивность только зарядов одного знака. Для зарядов разных знаков это свойство требует независимого исследования. Заряд системы частиц равен алгебраической сумме зарядов этих частиц Q = К фундаментальным свойствам заряда относится его сохранение, т. е. в любых процессах природы заряд изолированной системы материальных объектов не изменяется Qсист. = Существование в природе зарядов двух типов, обладающих свойством аддитивности (сложения), приводит к тому, что в сложных системах влияние зарядов частиц разных знаков, как правило, ослабляется. В макроскопических телах количество зарядов разных знаков обычно строго одинаково; за счёт большой подвижности электронов, которые тела приобретают или теряют. Такие тела принято называть нейтральными. Однако «истинно нейтральных» объектов в природе очень мало – на сегодняшний день это фотон и нейтрино. Опыты с нейтральными атомами и молекулами показали, что электрический заряд одинаков во всех инерциальных системах отсчёта. Следовательно, электрический заряд – это внутренне присущая частице характеристика; столь же фундаментальная, как и его масса.
 Приступая к поиску выражения для существующих внешних условий через характеристики системы заряженных частиц, рассмотрим систему неподвижных зарядов qi, положение которых в пространстве описывается радиус-вектором Приступая к поиску выражения для существующих внешних условий через характеристики системы заряженных частиц, рассмотрим систему неподвижных зарядов qi, положение которых в пространстве описывается радиус-вектором 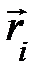 (рис. 9.1). Будем исследовать воздействие этой системы на неподвижный пробный заряд q о, помещённый вблизи этой системы в точке пространства с радиусом (рис. 9.1). Будем исследовать воздействие этой системы на неподвижный пробный заряд q о, помещённый вблизи этой системы в точке пространства с радиусом 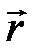 . Для определённости заряд q о принято считать положительным и малым; последнее оправдано тем, что внесение q о не искажает первоначальной конфигурации системы зарядов qi. . Для определённости заряд q о принято считать положительным и малым; последнее оправдано тем, что внесение q о не искажает первоначальной конфигурации системы зарядов qi.Объединим мысленно пробный заряд q о с остальными, получим систему из (N + 1) неподвижного заряда. Это позволяет применить к ней описание взаимодействия, принятое в системе взаимодействующих частиц (гл. 8 и [3, с. 27, 28]). Другими словами, все частицы системы рассматриваются как равноправные, взаимодействие каждой пары зарядов по закону Кулона происходит независимо от присутствия остальных зарядов. Из этого взаимодействия, где строго справедлив закон независимости действия сил, мы должны выделить характеристики, фиксирующие воздействие остальных зарядов системы на пробный заряд q о. Важнейшей из них является результирующая сила
здесь Каждый член суммы (9.2) в фиксированный момент времени зависит от расстояния между точечными зарядами, что олицетворяет концепцию «дальнодействия», в которой q о непосредственно взаимодействует с каждым qi из системы зарядов. Одновременно она позволяет рассматривать результирующую силу как векторное поле (§ 2.4), типичное для концепции близкодействия. Иными словами, изучение воздействия на пробный q о можно свести к изучению свойств поля сил. Однако не следует забывать, поле сил характеризует одновременно оба объекта – q о и qi, тогда как объективная физическая характеристика воздействия на любой пробный заряд q о со стороны окружения должна зависеть только от параметров этого окружения, но не зависеть от величины q о. Поскольку в формуле (9.2) каждый член суммы пропорционален q о, в качестве физической характеристики естественно выбрать величину, называемую электрическим полем:
Единицы измерения поля специальных названий не имеют; размерность поля есть [2]. Из определения следует, электрическое поле – это векторная функция, равная силе, действующей на единичный положительный пробный заряд, помещённый в точке пространства с радиус-вектором Естественно ожидать, на электрическое поле
сравнивая первую и вторую формулы выражения (9.4), для системы зарядов
9.2. Циркуляция электрического поля неподвижных Рассуждения в параграфе 9.1. привели нас к тому, что формулы (9.2) и (9.4) для произвольного движения зарядов неверны. Однако формула (9.3) сохраняет свой смысл и позволяет найти результирующую силу, если мы сможем научиться независимо находить поле Продолжая перенос на электрическое поле
этот контурный интеграл есть предел суммы Поскольку поля
Другими словами, поле неподвижных зарядов – безвихревое, потенциальное. Его силовые линии не обладают тенденцией к «закрученности». В параграфе 2.3, с. 31, было показано, затраченная работа
где
Эту величину принято называть потенциалом данной точки электростатического поля; потенциал j – фи равен работе по перемещению пробного заряда из данной точки поля в другую, где электростатическое поле отсутствует (r ® Разность потенциалов электростатического поля в точках
и не зависит от длины и формы пути. Чтобы найти явное выражение для потенциала j (r), создаваемого системой зарядов q1 …, qN, представленной на рис. 9.1., добавим, как это было сделано в параграфе 9.1, пробный заряд qо и найдём энергию взаимодействия изолированной системы из (N+1) зарядов; при этом будем учитывать энергию взаимодействия заряда qо только с N зарядами системы (см. рис. 9.1); взаимодействие между q1 …, qN зарядами нет смысла рассматривать (? ). Уточним энергию взаимодействия между двумя зарядами qo и qi. Из формулы (2.5) с. 30, следует Теперь учтём, что результирующая потенциальная сила F(r), действующая на пробный заряд qо со стороны системы зарядов q1 …, qN, равна, формула (2.5):
Иначе говоря, электрический потенциал равен потенциальной энергии воздействия системы зарядов на единичный пробный заряд, расположенный в точке r. Кроме того, электрический потенциал, как и напряжённость электрического поля, подчиняется принципу суперпозиции для системы зарядов и равен алгебраической сумме электрических потенциалов ji = k× qi/ri, создаваемых отдельными зарядами, т. е. j (r) = å ji(r). В заключение заметим, привлечение двухчастичного взаимодействия к изучению свойств электрического поля системы зарядов позволило, как и в механике, вычленить силовую характеристику поля – напряжённость
9.3. Поток вектора напряжённости. Закон Гаусса. До сих пор обсуждение свойств электрического поля проводилось на основе известных свойств ньютоновских сил взаимодействия зарядов. Чтобы двинуться далее в изучении специфических свойств электрического поля, предпримем усилия по его графическому представлению. Как и любое векторное поле, электрическое поле
 вида (9.4) и с учётом однородности электрических свойств пространства получим сферически симметричную картину силовых линий поля (рис. 9.3). Поскольку электростатическое поле исследуется посредством пробного положительного заряда qо, принято считать, что силовые линии направлены от заряда, если заряд q > 0, и к заряду, если q < 0. Ещё раз вспомним, силовое поле на рис. 9.3 сферически симметрично (ёжик защищается). вида (9.4) и с учётом однородности электрических свойств пространства получим сферически симметричную картину силовых линий поля (рис. 9.3). Поскольку электростатическое поле исследуется посредством пробного положительного заряда qо, принято считать, что силовые линии направлены от заряда, если заряд q > 0, и к заряду, если q < 0. Ещё раз вспомним, силовое поле на рис. 9.3 сферически симметрично (ёжик защищается).
Перейдём к графическому представлению электрического поля через его скалярную характеристику «потенциал». Для одного заряда q, помещённого в некоторую точку пространства, электрический потенциал, согласно формуле (9.10), принимает вид: j (r) = k× q/r. Потенциал электрического поля равен работе по перемещению единичного заряда (рис. 9.4) из бесконечности ( Эквипотенциальную поверхность можно провести через любую точку поля. Однако условились проводить поверхности таким образом, чтобы разность потенциалов для двух соседних поверхностей была одна и та же. Это позволяет по густоте эквипотенциальных поверхностей судить о величине силового поля (рис. 9.4); при приближении к заряду эквипотенциальные поверхности становятся гуще, напряжённость поля |Dj/Dr|, формула (9.7), увеличивается. Пытливый и настойчивый читатель в этом может убедиться, воспользовавшись уравнением (9.10) для единичного заряда q. При записи Dj потенциал желательно выразить через ri, а приращение Dri, определяющее r(i+1)-й радиус эквипотенциальной поверхности, будет задавать постоянство разности потенциалов ближайших эквипотенциальных поверхностей. Спрашивайте.
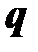 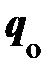 Проясним вопрос взаимного расположения силовых линий электростатического поля и эквипотенциальных поверхностей. На первый взгляд силовые линии должны быть перпендикулярны эквипотенциальным поверхностям, а графическое представление векторного Проясним вопрос взаимного расположения силовых линий электростатического поля и эквипотенциальных поверхностей. На первый взгляд силовые линии должны быть перпендикулярны эквипотенциальным поверхностям, а графическое представление векторного  и скалярного j полей (рис. 9.4) не противоречит такому предположению. и скалярного j полей (рис. 9.4) не противоречит такому предположению.
Пусть в поле заряда q совершается работа по перемещению пробного заряда qо из точки 1 в точку 2 (рис. 9.5.). Вспомним, при выводе уравнения (9.7) мы воспользовались тем, что по определению элементарная работа: dA = = F× dS× cosa. Проецируя это уравнение на электростатическое поле, dA = = qо× Е× dS× cosa. Вместе с тем, элементарная работа может быть записана через изменение потенциальной энергии dW, взятой с противоположным знаком, т. е. dA = – dW = = – qо× dj. Приравнивая между собой правые части уравнений для элементарной работы, получаем выражение: qо× Е× dS× cosa = qо× dj. Левую и правую части выражения можно сократить на qо, а приняв во внимание, что перемещение осуществляется по поверхности одинакового потенциала, т. е. dj = 0, приходим к уравнению вида: Е× dS× cosa = 0. Равенство нулю выполняется только в том случае, если cosa = 0, что возможно при a = 0. Таким образом, векторное и скалярное поля неподвижных зарядов взаимно перпендикулярны. Итак, графическое отображение силового электрического поля неподвижных зарядов стимулировало появление понятия силовой линии. Усилия по отображению скалярного (потенциального) поля привели нас к мысли, что густота эквипотенциальных поверхностей позволяет судить о величине силового поля (с. 135). Таким образом, через силовые линии мы можем судить не только о направлении поля заряда, но и о его величине. Иначе говоря, в безвихревом, потенциальном поле появляется новая характеристика, связанная как-то с числом силовых линий, пронизывающих некую замкнутую поверхность S, охватывающую электрические заряды. Так появляется ещё одна характеристика поток электрического поля неподвижных зарядов, которая на символическом языке (аналитически) может быть записана из следующих соображений. Для простоты прежде начнём рассмотрение поля одного заряда q (рис. 9.6). Из формулы (9.4) следует, модуль вектора напряжённости Выделим на поверхности сферы (рис. 9.6, справа) площадку dS, Пронизывающие её силовые линии поля dN образуют элементарный поток электрического поля через эту площадку; иными словами, элементарный поток вектора напряжённости электрического поля. Очевидно, что этот поток определяется числом силовых линий, приходящихся на единицу поверхности, и элементарной площадкой dS. В качестве числа силовых линий, приходящихся на единицу поверхности, может выступать вектор напряжённости электрического поля
Из формулы (9.11) следует, электрический заряд характеризует интенсивность «источника» электрического поля, а знак заряда определяет и знак источника поля. Другими словами, электрическое поле – это векторное поле с источниками, силовые линии этого поля начинаются и заканчиваются на заряде, а число силовых линий пропорционально величине заряда, характеризующей тенденцию поля к истечению. 9.4. Применение закона Гаусса для расчёта

Полученные в предыдущем параграфе результаты, формула (9.11), обобщим теперь на замкнутую поверхность произвольной формы. Вычислим для этого элемент потока DNE вектора напряжённости  через элемент этой произвольной поверхности DS (рис. 9.7.), определяемой радиус-вектором через элемент этой произвольной поверхности DS (рис. 9.7.), определяемой радиус-вектором 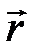 . Поскольку нормаль к произвольной поверхности (рис. 9.7) не совпадает с направлением вектора напряжённости, пронизывающего поверхность сферы, поток силового поля неподвижного заряда будет находиться через скалярное произведение: . Поскольку нормаль к произвольной поверхности (рис. 9.7) не совпадает с направлением вектора напряжённости, пронизывающего поверхность сферы, поток силового поля неподвижного заряда будет находиться через скалярное произведение:
DNE = (E× DS) = E× DS× cosa. (9.12) Почему? Здесь DS× cosa (см. рис. 9.7.) – это проекция элемента площадки DS произвольной поверхности на элемент DS ¢ сферы радиуса DNE = Ранее, в работе [3, с. 13] мы убедились в том, что при малых линейных углах отношение длины дуги к радиусу, образующему эту дугу, отражает значение этого угла, т. е. Dj @ Ds/R. Естественно ожидать, что элементарная площадка DS ¢ = DS× cosa опирается на телесный угол DNE = k× q1× Иными словами, для одного заряда элемент потока электрического поля DNE через произвольно ориентированный элемент поверхности DS зависит не только от величины заряда, но и от того телесного угла Для потока NE через произвольную замкнутую поверхность соответственно имеем уравнение вида:
где W – полный телесный угол, под которым видна окружающая заряд q1 поверхность. Очевидно, если заряд находится внутри замкнутой поверхности S, то она окружает его со всех сторон и видна со стороны заряда, независимо от её формы, под телесным углом W = 4p стерадиан (семечко «видит» поверхность яблока под углом 4p Ср.). Перейдём от одного заряда к системе зарядов qi. Разумеется, все заряды одновременно поместить в начало отсчёта нельзя. Теперь это и не нужно, поскольку охватывающая каждый заряд поверхность может быть любой. Каждый заряд создаёт своё поле Еi, а поскольку для электрического поля Е справедлив принцип суперпозиции, его поток аддитивен, т.е. NE =
при этом алгебраическая сумма справа распространяется лишь на заряды, расположенные внутри поверхности S. Формула (9.15) выражает собой закон Гаусса-Остроградского: для произвольной системы неподвижных зарядов поток вектора напряжённости электрического поля через произвольную замкнутую поверхность пропорционален величине электрического заряда, заключённого внутри этой поверхности. Этот же закон для непрерывно распределённых зарядов принимает вид:
здесь, соответственно, rq – объёмная плотность электрического заряда, равная q/V; sq – поверхностная плотность электрического заряда, равная q/S; t – линейная плотность электрического заряда, равная q/ Приведённые здесь рассуждения указывают на то, что поток поля сам по себе не отражает все свойства поля и тем самым ограничивает применение закона Гаусса необходимостью привлекать дополнительно соображения симметрии. Рассмотрим пример вычисления вектора напряжённости E электрического поля сферы радиуса R, заряженной по объёму с плотностью rq = const (рис. 9.8). Решение: Если сфера заряжена положительно, силовые линии направлены как внутри, так и вне сферы по радиусу от центра; это следует из соображений симметрии. Поскольку вычисление потока
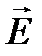 запишется NE = = Е× S = 4pk× Dq( r ) (9.15), где Dq( r ) – доля заряда, оказавшаяся внутри поверхности сферы интегрирования r < R; её придётся выражать через полный заряд q сфер R. Заряд Dq( r ) через плотность rq запишется Dq( r ) = rq× запишется NE = = Е× S = 4pk× Dq( r ) (9.15), где Dq( r ) – доля заряда, оказавшаяся внутри поверхности сферы интегрирования r < R; её придётся выражать через полный заряд q сфер R. Заряд Dq( r ) через плотность rq запишется Dq( r ) = rq× 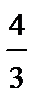 × p× r3; найдём rq через полный заряд сферы с радиусом R. Пусть этот заряд равен q, тогда rq = = q / × p× r3; найдём rq через полный заряд сферы с радиусом R. Пусть этот заряд равен q, тогда rq = = q / 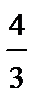 × p× R3, отсюда немедленно следует, что Dq( r ) = rq× × p× R3, отсюда немедленно следует, что Dq( r ) = rq× 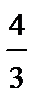 × p× r3 = (q / × p× r3 = (q / 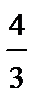 × p× R3)× × p× R3)× 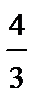 × p× r3 = (q× r3) / R3. Подставим это в поток поля формулы (9.15), NE = = Е× S = 4pk× Dq( r ) = 4pk× (q× r3) / R3.Отсюда следует: Е = × p× r3 = (q× r3) / R3. Подставим это в поток поля формулы (9.15), NE = = Е× S = 4pk× Dq( r ) = 4pk× (q× r3) / R3.Отсюда следует: Е =  = = 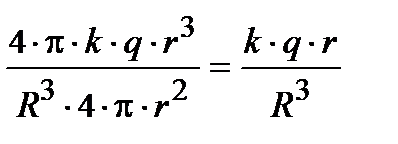 . Умножив числитель и знаменатель на . Умножив числитель и знаменатель на 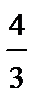 × p и приняв к сведению, что q / × p и приняв к сведению, что q / 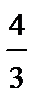 × p× R3 равно плотности заряда сферы rq, пытливый читатель получит выражение напряженности поля Е = × p× R3 равно плотности заряда сферы rq, пытливый читатель получит выражение напряженности поля Е =  внутри сферы радиуса r < R. Проделали? Результатом является вывод – поле внутри сферы зависит от радиуса линейно; можно построить график Е(r); r изменяется от нуля до R. внутри сферы радиуса r < R. Проделали? Результатом является вывод – поле внутри сферы зависит от радиуса линейно; можно построить график Е(r); r изменяется от нуля до R.
Настойчивый читатель может самостоятельно найти выражение для вектора напряжённости Популярное:
|
Последнее изменение этой страницы: 2017-03-11; Просмотров: 613; Нарушение авторского права страницы