
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Уравнение переноса в газах. Диффузия
В предыдущем параграфе, и не только [3, с. 51..; 57..], нам удалось показать – главным в тепловом равновесии любого макрообъекта является только то, чтобы между частицами были какие-либо столкновения, приводящие к «хаотизации» их движения. Процесс приближения к тепловому равновесию происходит постепенно через ряд стадий. Этим стадиям соответствуют различные типы воздействий, ведущие к установлению теплового равновесия. При этом могут происходить следующие процессы. Если значения давления газа в его различных областях объёма не совпадают, то на микроуровне происходит передача импульса от одной области газа к другой, ведущая к установлению одинакового давления. В результате устанавливается механическое равновесие. Однако при этом внутренние энергии этих двух областей газа могут не совпадать, если их температуры различны. В течение какого-то промежутка времени после установления равенства давлений из-за хаотических столкновений молекул имеет место энергетическое воздействие одной области газа на другую. На микроуровне это означает, молекулы «горячего» газа, обладающего большей средней энергией, переносят её молекулам «холодного» газа. Происходит передача внутренней энергии на микроуровне от одной области газа к другой, ведущая к установлению одинаковой температуры. Существует третья возможность внешнего воздействия одной области объёма газа на его другую область. Её можно реализовать, когда наряду с обменом импульсом и внутренней энергией частей газа может происходить обмен входящими в эти части газа молекулами. Если при этом газы в этих частях разного сорта, то такое корпускулярное воздействие приводит к установлению одинаковых концентраций каждого газа в его частях. При этом происходит передача числа частиц каждого сорта на микроуровне от одной части газа к другой. Этот процесс происходит медленно и возможен даже тогда, когда давление и температура в этих частях уже стали одинаковыми. Таким образом, процессы установления теплового равновесия в результате силового, энергетического и корпускулярного контактов называются явлениями переноса. Как следует из приведённого на знаковом (словесном) языке анализа, к ним относятся явления переноса импульса, энергии и числа частиц (или массы).
           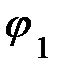 Итак, названные явления обусловлены переносом молекулами газа соответствующих физических характеристик: массы при диффузии; импульса при вязком трении; энергии при теплопроводности. Механизм явлений единый – столкновительный и изучить эти явления, это значит – установить закон которому они подчиняются. Наиболее удобной характеристикой такого процесса может служить поток физической характеристики, переносимый молекулами через площадку DS в направлении оси х – Итак, названные явления обусловлены переносом молекулами газа соответствующих физических характеристик: массы при диффузии; импульса при вязком трении; энергии при теплопроводности. Механизм явлений единый – столкновительный и изучить эти явления, это значит – установить закон которому они подчиняются. Наиболее удобной характеристикой такого процесса может служить поток физической характеристики, переносимый молекулами через площадку DS в направлении оси х –  (рис. 7.6). Здесь N и j соответственно число частиц и переносимая ими физическая характеристика. Общую формулу потока (рис. 7.6). Здесь N и j соответственно число частиц и переносимая ими физическая характеристика. Общую формулу потока  при малых отклонениях от равновесия можно предугадать, исходя из следующих соображений. Известно [3, с. 53], что за время Dt через площадку DS в одном из направлений, в частности, в направлении оси х, движется N = при малых отклонениях от равновесия можно предугадать, исходя из следующих соображений. Известно [3, с. 53], что за время Dt через площадку DS в одном из направлений, в частности, в направлении оси х, движется N = 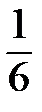 n× u× DS× Dt молекул. Численное значение физической величины, переносимой молекулами в направлении оси х из точки (х – l) через площадку DS (рис. 7.6), запишется: (N× n× u× DS× Dt молекул. Численное значение физической величины, переносимой молекулами в направлении оси х из точки (х – l) через площадку DS (рис. 7.6), запишется: (N×  )1 = )1 = 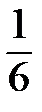 (n× (n×  )1× u× DS× Dt. В обратном направлении через эту же площадку из точки (х + l) перенос физической величины (N× )1× u× DS× Dt. В обратном направлении через эту же площадку из точки (х + l) перенос физической величины (N×  )2 = )2 = 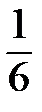 (n× (n×  )2× u× DS× Dt. Каждый процесс переноса связан с отклонением физической величины (n× )2× u× DS× Dt. Каждый процесс переноса связан с отклонением физической величины (n×  )i от равновесного значения и поток физической величины D(N× )i от равновесного значения и поток физической величины D(N×  ) через площадку DS в направлении оси х запишется: D(N× ) через площадку DS в направлении оси х запишется: D(N×  ) = – {(N× ) = – {(N×  )2 – (N× )2 – (N×  )1}. Если учесть число частиц, соответственно дальше и ближе точки х, и среднюю скорость их хаотического движения последнее равенство принимает вид: )1}. Если учесть число частиц, соответственно дальше и ближе точки х, и среднюю скорость их хаотического движения последнее равенство принимает вид: D(N× Учтём теперь тот факт, что перед пересечением площадки каждая молекула испытывает последнее столкновение, т. е. обменивается физической характеристикой с другими молекулами, на расстоянии не меньшем l от точки х; где l – длина её свободного пробега (рис. 7.6). У нас появляется возможность представить отклонение физической величины D(N×
Если учесть, что 2l это не что иное как D х, в чём пытливый студент может легко убедиться, глядя на рис. 7.6 (преобразования проделали? ), приходим к уравнению, отражающему темп отклонения D(N×
здесь под символом u подразумевается средняя квадратичная скорость молекулы (? ); формула (7.5). Итак, нам удалось, не в ущерб математической строгости, прописать явления переноса и получить уравнение, аналогичное уравнению Фика. Дальнейший анализ формулы (7.13) позволит найти конкретные формулы для явлений переноса. В заключение преобразований следует заметить, что за действием умножения на 2l скрывается математическая операция по нахождению приблизительного приращения функции, равного произведению производной на приращение аргумента. Приступая к описанию явления диффузии, рассмотрим газовую смесь, состоящую из молекул двух сортов n1 и n2. Для упрощения расчётов будем считать, что молекулы обеих компонент мало отличаются по массе, т. е. m1
Здесь D – коэффициент диффузии, равный
Популярное:
|
Последнее изменение этой страницы: 2017-03-11; Просмотров: 702; Нарушение авторского права страницы