Прямолинейное равномерное движение

⇐ ПредыдущаяСтр 2 из 17Следующая ⇒

Неотъемлемым свойством материи является движение. Простейший вид движения материи – механическое движение – представляет собой изменение положения тела в пространстве относительно других тел с течением времени. Издавна человечеству приходилось решать задачу, «где и когда будет находиться движущееся тело? ». Так, войны-разведчики припадали ухом к Земле и, слушая стук копыт конницы врага о Землю, определяли положение противника (в символическом представлении, например, – х, s) и время приближения его к тем или иным рубежам защиты (в символическом представлении – t). Они решали основную задачу кинематики (раздела механики), где и когда будет находиться противник, если известен закон его движения: ; в символической записи под f «скрываются» кинематические характеристики передвижения объекта, в частности, конницы. Естественно, в настоящее время такого рода задача решается другими методами. Однако, знать закон движения тела, это значит знать, как, по какому закону изменяется положение движущегося тела в пространстве с течением времени. Для этого нужно научиться вычленять кинематические характеристики, через которые проявляется движение тела; как эти характеристики связаны с пространственными и временными характеристиками в символической записи.

Первое, что нужно сделать для того, чтобы знать закон движения тела, это научиться определять положение тела в пространстве; на плоскости или прямой. Во времена Ньютона, когда закладывались основы научного познания, было известно, декартова система координат, где все три оси имеют одинаковую размерность расстояния, является математическим отражением трёх мерности физических объектов. Она годится и для определения положения движущегося тела в пространстве. Почему?

При движении тела все его точки движутся по одинаковым линиям-траекториям, разделённым пространственно; попробуйте представить на рисунке. В связи с этим, для аналитического описания движения тела в зависимости от условий конкретной задачи, механика (раздел физики) использует разные физические модели, упрощающие описание движения тел. Так, модель абсолютно твёрдого тела предполагает, пренебрежимо малая роль деформации при движении тела в определённых условиях даёт возможность рассматривать его как абсолютно твёрдое. Например, Ваша правая рука вместе с Вами не опоздала на занятия. Здесь немедленно появляется ещё одна модель – материальная точка – тело, размерами которого в условиях данной задачи можно пренебречь. Это возможно хотя бы потому, что все точки тела движутся по одинаковым линиям-траекториям, что значительно упрощает определение положения движущегося тела.

Рис. 1.1.

Рис. 1.2.

Трёх мерная система координат (декартова) представлена на рис. 1.1. Пусть движущееся тело, например, Вы пытаетесь не опоздать на занятия, находится в точке А; координаты положения можно определить, если задать единицы измерения по осям, что в символическом представлении может быть представлено А(х, у, z). Ориентируясь, где Вы находитесь и в какое время, можете определить – опаздываете или придёте в назначенное время. Из рис.1.1. следует, положение тела может быть однозначно (почему? ) определено тройкой чисел (х, у, z); в пространстве двумерном или одномерном, соответственно, двумя или одним числом. Отобразите это на рисунке.

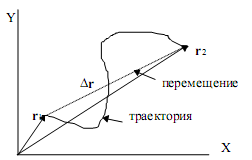
Задать положение тела можно не только координатами х, у, z, но и радиус-вектором ( ), что и представлено на рис.1.2. Здесь вектора определяют, соответственно, начальное и конечное положения движущегося тела.

Настало время задаться вопросом, а какое тело является телом отсчёта в приведённом выше примере? Решение приняли? Правильно! Ответ не однозначен. Тогда подискутируйте с товарищем: он в аудитории поджидает Вас, а Вы приближаетесь; можно и наоборот, Вы заботитесь, чтоб не опоздать.

Чтобы перейти к аналитическому описанию движения тел, а именно, к поиску характеристик, проясняющих свойства движения, следует уточнить вопрос о субординации в соотношениях между «пространством» и «движением». Создатель неевклидовой геометрии, наш соотечественник Н. Лобачевский, по этому поводу писал: «В природе мы познаем собственно только движение, без которого известные впечатления не возможны. Все прочие понятия, например, геометрические, произведены нашим умом искусственно, будучи взятые в свойствах движения; поэтому пространство само по себе отдельно для нас не существует». Следовательно, геометрические свойства пространства порождены соответствующими свойствами движения материи. Здесь пространство, как физическая реальность, выступает в качестве внешнего объекта, который воспринимается, наблюдается и измеряется и с помощью которого теоретически могут быть познаны свойства движения. Время также внешняя сторона движения материи, через которую проявляется движение; оно воспринимается, наблюдается и измеряется. Свойства пространства и времени предопределяются соответствующими свойствами движения. И такая связь свойств пространства и времени со свойствами движения доказывается успехами физики. В частности, «специальной теорией относительности», которая, по существу, является физической теорией пространства и времени.

Приступая к аналитическому описанию движения тел, следует осознавать, любое движение можно представить как комбинацию поступательного и вращательного движений. Поступательным принято называть такое движение, при котором прямая, соединяющая две любые точки движущегося теле, остаётся параллельной самой себе; отобразите это на рисунке. При вращательном движении все точки тела движутся по кривым некоторого радиуса, центры которых лежат на одной прямой, называемой осью вращения; представьте образ траектории данного движения на рисунке.

Для аналитического описания движения тела, необходимо условиться, относительно какого тела будет отсчитываться изменение положения движущегося тела. С этим телом связывается система координат (декартова, прямоугольная), позволяющая определить положение движущегося тела в пространстве (на плоскости, прямой, если тело движется в пространстве соответствующей размерности). Время, равно как и пространство, неотъемлемая форма существования материи. Естественно, для описания движения во времени необходимо научиться отсчитывать время. Человечество научилось его отсчитывать, «поймав» биологическую (и не только) цикличность. Всё это – тело отсчёта, система координат и время – образует систему отсчёта и позволяет приступить к вычленению свойств, через которые проявляется, в частности, поступательное движение тел. Эти свойства, представленные в символической форме, позволяют через количественную математику отобразить изменение положения движущегося тела в пространстве с течением времени. Как количественная математика позволяет это сделать?

Двигаясь в пространстве, материальная точка проходит через ряд точек. Если эти точки соединить, получится линия, которую принято называть траекторией движения; см. рис. 1.2. и рис. 1.1. Длина траектории представляет собой пройденный путь, в символическом представлении S, и является скалярной величиной. Наряду с понятием «пройденный путь» в кинематике используется понятие «вектор перемещения». Это величина векторная, в символическом представлении D или D . Вектор перемещения D представляет собой направленный отрезок прямой, соединяющий начальное положение движущейся точки с её конечным положением. Проведите вектор перемещения D на рис.1.1., считая начальной точку В, а конечной (·А); или, соответственно, (·С) ® (·В). Модуль вектора перемещения D , представленного в двумерном пространстве на рис. 1.2., можно выразить через координаты: Таким образом, модуль вектора перемещения через количественную математику связан с изменением координат тела при движении. Количественная математика здесь представлена теоремой Пифагора, а в изменении положения по координатным осям х и у вычитанием из конечного положения начального. Запишите, например, модуль вектора (см. рис. 1.2.) через изменение координат.

Приведённые примеры количественной математики показывают, для получения аналитического уравнения, отражающего движение тела во времени, нужно искать кинематические характеристики «чувствительные» к времени. Попробуем это проделать.

Переходя с одной стороны улицы на другую, мы следим за тем, как движется транспортный поток. При оценке ситуации наша внутренняя речь привлекает слова быстро, медленно, что означает безопасно или нет (успею или не успею перейти). За словами «быстро», «медленно» также скрывается быстрота изменения положения движущегося тела, то есть его вектора перемещения или пройденного пути S, за время наблюдения. Естественно, за время сделанного пешеходом шага средство передвижения успевает переместиться не на расстояние шага. В символическом представлении это может выглядеть так: . Так появляется кинематическая характеристика быстроты изменения положения тела в пространстве – скорость; символически обозначается буквами Если мы знаем перемещение , совершённое движущимся телом за время t, скорость находится операцией деления (почему? ) количественной математики: . Естественно ожидать, скорость величина векторная, поскольку характеризует быстроту изменения вектора перемещения, и её направление совпадает с направлением вектора перемещения. Математическая операция деления вектора на скаляр не препятствует такому выводу.

Если движение равномерное, аналитически закон движения имеет вид: . Простота закона кажущаяся. Убедитесь на дежурной задаче. Со станции вышел товарный поезд, идущий со скоростью 36 км/ч. Через 30 мин по тому же направлению вышел экспресс, скорость его 72 км/ч. Через какое время после выхода товарного поезда и на каком расстоянии от станции, экспресс нагонит товарный поезд? Решить задачу также графически. Чтобы решить задачу аналитически, нужно составить уравнения, отражающие движение тел (товарного и экспресс поезда). Это первая трудность; в математике дают уравнения, содержащие неизвестное и есть алгоритм их решения; здесь же нужно составить уравнения самостоятельно, учитывая условие задачи, и только потом приступать к решению. Составьте эту систему (из двух) уравнений и решите её относительно неизвестного. Приступая к решению задачи графически, выберите систему координат, которая обеспечит решение. Непонятно? Вернитесь к условию задачи, оно подскажет; возможно, придётся сделать не один чертёж. Особое внимание обратите на вопрос «через какое время… и на каком расстоянии». Наверное, догадались, придётся записать х = f(t), а закон движения задан? Снова в условие, нашли ключевые слова «идущий со скоростью; скорость его». Записали уравнения движения товарного?; запишите и для экспресса, не забывая, вышел через… Стало очевидным?; строить придётся в системе координат (х, t).

В кинематике неравномерного поступательного движения очень часто используется понятие средней скорости. Под средней скоростью понимают скорость некоего равномерного движения, при котором тело проходит тот же путь и за то же самое время, за которое оно прошло тот же путь, но при переменном равномерном поступательном движении. Аналитически это записывается так: . Простота записи опять же кажущаяся. Убедитесь. Если это просто, можно порадоваться за Вас! Один электровоз прошёл половину пути со скоростью 80 км/ч, а другую половину со скоростью 40 км/ч. Другой электровоз шёл половину времени со скоростью 80 км/ч, а половину времени со скоростью 40 км/ч. Какова средняя скорость каждого электровоза? Не забудьте записать «дано», поможет ориентироваться в заданных величинах. Это в свою очередь обеспечит правильное составление уравнений. Не забудьте, здесь два условия, должно быть два чертежа, естественно, и два решения.

Завершая экскурс в раздел кинематики «прямолинейное равномерное движение», перечислим его ключевые слова: движение, пространство, время, система отсчёта, координата, траектория, перемещение, скорость, закон движения.

⇐ Предыдущая 123 4 5 6 7 8 9 10 Следующая ⇒