
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Предмет физики. Связь физики с другими наукамиСтр 1 из 17Следующая ⇒
Я.Д. Лебедев
ПРОПЕДЕВТИЧЕСКИЙ КУРС ПО ФИЗИКЕ
Утверждено редакционно-издательским советом в качестве учебного пособия
Вологда УДК 53/075 ББК 223я73 Л33
Рецензенты: Ю.А. Сауров, доктор педагогических наук, профессор, член-корреспондент РАО (г. Киров), Л.А. Минасян, доктор философских наук, профессор, кафедра физики, кафедра кристаллографии и экспериментальной физики ГУ им. Лобачевского, Нижний Новгород
Лебедев, Я.Д. Л33 Пропедевтический курс по физике: учебное пособие / Я.Д. Лебедев. – Вологда: ВоГУ, 2014. – 85 с.
Данный пропедевтический курс написан в соответствии с программой курса физики для технических специальностей в вузах и направлен на оказание помощи студентам в освоении физики высшей школы. Пособие включает содержание физики средней и высшей школы. Оно направлено на формирование у студентов понимания: знакового (словесного) языка и на его основе приобретение навыков построения моделей реальности; кодирования содержания курса через символический язык с целью перехода на язык математики и, владея навыками преобразования информации курса физики и математических действий, уметь получать оценочный результат. Пособие предназначено для студентов факультета промышленного менеджмента и инновационных технологий.
УДК 53/075 ББК 223я73
© ВоГУ 2014 © Лебедев Я.Д., 2014 Пропедевтический курс физики для студентов факультета промышленного менеджмента и инновационных технологий представлен с целью оказания помощи в изучении основ физики высшей школе, который изучается со второго по четвёртый семестр (18/18/18; 16/16/16; 18/18/18). Такая необходимость возникла после того, когда обучение в школе достигло такого уровня, что будущие студенты технического вуза не владеют многими элементами знаний по математике, а вместе с этим и по физике. Причина здесь кроется не только в учащихся, но и в формируемой государством системе образования, что и подвигло авторов к таким действиям. Не последнюю роль сыграло и то, что существующие учебные пособия современное студенчество читать не только не хочет, но и не может. В связи с этим основная задача предлагаемого пособия, убедить студента в том, что он всё-таки может научиться читать техническую литературу. Естественно, при некотором напряжении с его стороны. Читать техническую литературу нелегко. Человек, являясь универсальным инструментом, созданным Реальностью для очевидных целей, вынужден отражать её, Реальность, в знаках (словах), образах, символах и действиях. Всё это проявляется в концептуальном аппарате науки и заканчивается воздействием на Реальность. Физика не исключение, а математический аппарат, являющийся её языком, позволяет получать количественные оценки, заканчивающиеся преобразованием окружающей реальности. Причём не только с грубой материей. Поскольку физика является прародительницей не только новых наук, но и новых отраслей производства, естественно желание освоить «языки» представления этого знания. Пропедевтический курс направлен на то, чтобы помочь студентам в освоении этих языков представления знания – языков мышления человека. В пособие включены элементы содержания классической механики и термодинамики. Отведённое на пропедевтический курс число часов (16/16), даёт надежду на понимание связи языков представления содержания. Выбор материала позволяет надеяться на ознакомление и с основами дифференциально-интегрального исчисления. На лекциях поднимаются вопросы, способствующие пониманию реализации обозначенных желаний. На практических занятиях работа направлялась по их возможной практической реализации. Всё это должно подкрепляться самостоятельной работой студента над домашними заданиями по решению задач. Задания содержат методическое обеспечение, направленное на оказание помощи в понимании условия задачи и нахождения возможных путей её решения при использовании упомянутых языков мышления. Для дистанционного обучения подготовлены подсказки пошаговые, до конечного решения.
ОГЛАВЛЕНИЕ 1. Кинематика поступательного и вращательного движения 5 1.1. Предмет физики. Связь физики с другими науками 5 1.2. Прямолинейное равномерное движение 6 1.3. Прямолинейное равнопеременное движение 11 1.4. Вращательное движение 12 2. Динамика Ньютона 15 2.1. Современная трактовка законов Ньютона 15 2.2. Силы в механике. Практическое применение законов Ньютона 18 2.3. Понятие механического состояния. Работа. Мощность. Энергия 23 2.4. Законы сохранения в механике. Условия равновесия 26 3. Гармонические колебания. Волновые процессы 29 3.1. Сведения о колебаниях. Гармонические колебания 29 3.2. Уравнение колебания. Скорость. Ускорение. Квазиупругая сила 31 3.3.Связь параметров колебательной системы с периодом колебаний. Энергия колебательной системы с одной степенью свободы 33 3.4. Понятие сплошной среды. Колебания в сплошных средах. Понятие волны. Основные определения. Уравнение волны. 35 4. Элементы механики сплошных сред: жидкости и газы 40 4.1. Давление в жидкости и газе. Выталкивающая сила 40 4.2. Неразрывность потока. Уравнение Бернулли 43 4.3. Давление под искривлённой поверхностью жидкости. Капиллярные явления 47 5. Тепловые явления. Термодинамический и статистический методы исследования 50 5.1. Термодинамический и статистический методы исследования. Давление и внутренняя энергия идеального газа 50 5.2. Распределение энергии по степеням свободы. Закон парциальных давлений 53 5.3. Барометрическая формула 55 6. Термодинамика. Первое начало термодинамики 59 6.1. Некоторые общие понятия термодинамики 59 6.2. Внутренняя энергия термодинамической системы. Первое начало термодинамики 61 6.3. Работа в термодинамике 63 7. Изопроцессы и первое начало термодинамики 65 7.1. Внутренняя энергия и теплоёмкость идеального газа 65 7.2. Изопроцессы в идеальном газе; теплоёмкость газов 66 7.3. Адиабатический процесс 71 8. Круговые процессы 74 8.1. Замкнутые циклы. К.П.Д. цикла 74 8.2. Цикл Карно. К.П.Д. цикла. Второе начало термодинамики 76 8.3. Понятие энтропии 79 9. Библиографический список 84 И вращательного движения
Вращательное движение Вращательное движение является частным случаем криволинейного движения. Кроме того, будем рассматривать движение материальной точки по окружности с постоянной по модулю скоростью, Пусть точечное тело (материальная точка) движется по окружности радиуса R (рис. 1.3). За некоторый промежуток времени Dt оно пройдёт путь DS, равный дуге АВ. В точке А тело имело скорость
 . Геометрическая иллюстрация вращательного движения (рис. 3) позволяет эту запись представить следующим образом: . Геометрическая иллюстрация вращательного движения (рис. 3) позволяет эту запись представить следующим образом:  . Прочитать её можно так: вектор . Прочитать её можно так: вектор  , характеризующий изменение скорости по направлению, представляет собой сумму векторов ( , характеризующий изменение скорости по направлению, представляет собой сумму векторов (  ) и (– ) и (–  ) и соединяет начало первого вектора ( ) и соединяет начало первого вектора (  ) с концом второго вектора (– ) с концом второго вектора (–  ), рис. 1.3. Это позволяет выразить модуль, численное значение вектора ), рис. 1.3. Это позволяет выразить модуль, численное значение вектора 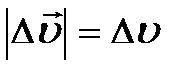 через кинематические характеристики: скорость и радиус окружности. Действительно, Ð АОВ = Ð ВСD как углы с взаимно перпендикулярными сторонами (построением убедились?; можно рассуждениями); по числовому значению скорость постоянна и через кинематические характеристики: скорость и радиус окружности. Действительно, Ð АОВ = Ð ВСD как углы с взаимно перпендикулярными сторонами (построением убедились?; можно рассуждениями); по числовому значению скорость постоянна и  . Следовательно, rАОВ и rВСD подобны по двум сторонам и углу между ними (почему? ), отсюда из rВСD следует . Следовательно, rАОВ и rВСD подобны по двум сторонам и углу между ними (почему? ), отсюда из rВСD следует  , а из rАОВ этот же угол , а из rАОВ этот же угол  (см. рис. 1.3.). Поскольку левые части уравнений равны (углы с взаимно перпендикулярными сторонами), то из правых частей немедленно следует, модуль, численное значение вектора (см. рис. 1.3.). Поскольку левые части уравнений равны (углы с взаимно перпендикулярными сторонами), то из правых частей немедленно следует, модуль, численное значение вектора  (самостоятельно проделали? ). По определению ускорение, в нашем случае характеризующее изменение скорости по направлению, равно (самостоятельно проделали? ). По определению ускорение, в нашем случае характеризующее изменение скорости по направлению, равно  . Если промежуток времени Dt взять малым, то хорда АВ стремится к длине дуги АВ, или пройденному пути DS за время Dt. Перепишите на листке аналитическое выражение ускорения (а) и самостоятельно замените в нём . Если промежуток времени Dt взять малым, то хорда АВ стремится к длине дуги АВ, или пройденному пути DS за время Dt. Перепишите на листке аналитическое выражение ускорения (а) и самостоятельно замените в нём 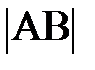 на пройденный путь DS. Поскольку DS/Dt = на пройденный путь DS. Поскольку DS/Dt =  , для символической записи ускорения, характеризующего быстроту изменения скорости по направлению, получим выражение , для символической записи ускорения, характеризующего быстроту изменения скорости по направлению, получим выражение  (преобразования проделайте самостоятельно). Направление центростремительного ускорения можно определить по рис. 1.3. Из треугольника скоростей, rВСD следует, чем меньше промежуток времени Dt, тем меньше угол Dj. При этом векторы (преобразования проделайте самостоятельно). Направление центростремительного ускорения можно определить по рис. 1.3. Из треугольника скоростей, rВСD следует, чем меньше промежуток времени Dt, тем меньше угол Dj. При этом векторы  и и 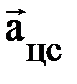 , имеют одинаковое направление и направлены по радиусу R окружности к её центру O. , имеют одинаковое направление и направлены по радиусу R окружности к её центру O.
При рассмотрении равномерного движения по окружности привлекались как линейные кинематические характеристики перемещение, путь, скорость, ускорение, радиус окружности, так и угловая характеристика – угол поворота Dj, опирающийся на отрезок АВ. Появление угла поворота связано с линейными величинами, естественно желание прописать равномерное движение материальной точки по окружности и через угловые характеристики. При вращательном движении угол поворота является основной кинематической характеристикой и с точки зрения количественной математики в общем виде может быть записан следующим образом: Dj = = j2 –.j1 = j2 = j = 2× p× N; если j1 = 0. Прочитаем эту запись: изменение угла поворота Dj равно разности конечного (j2) и начального (j1) значений; если же начальный угол j1 = 0, обозначать конечное значение значком j2 не имеет смысла и цифру два опускают. Итак, угол поворота j = 2× p× N, естественно, это произошло за время Dt; здесь 2p = 360о и представляет собой один полный оборот, N – число оборотов за время движения; не обязательно полных, например, 0, 37. Отношение угла поворота к времени, в течение которого это изменение произошло, будет характеризовать изменение угла поворота в единицу времени, то есть это быстрота изменения угла поворота или угловая скорость w. Аналитически это может быть представлено следующим образом: Ещё две характеристики, полезные для технических целей, могут быть введены из уравнения: j = 2p× N = w× t. Действительно, если N = 1, уравнение примет вид: 2p× 1 = w× t. Здесь t время одного полного оборота. Его принято обозначать буквой Т – время одного оборота. Тогда 2p = w× Т, отсюда следует Для снятия сомнений в понятии «малые углы», проделайте следующие действия: воспользуйтесь тригонометрической таблицей или калькулятором и найдите sin10о. Нашли? Запишите это значение. Проделайте следующие действия: 2p радиан равны 360о; найдите операцией «деление» сколько в одном градусе радиан; нужно 2p разделить на 360о, разделили?; не забыли, что p = 3, 14 радиан?; умножьте на 10о. Если уже умножили, сопоставьте с табличным результатом или найденным по калькулятору. В каком знаке ошибка? Вы с такой точностью умеете считать? Можно ли согласиться с понятием «малые углы»? Наверное, всё-таки можно! В заключение две дежурные задачи. Запишите центростремительное ускорение через угловую скорость; период обращения, частоту вращения. Введение угловых характеристик позволяет записать уравнение движения тела по окружности через угловые характеристики. Как будет выглядеть уравнение движения: j = f(t) через угловую скорость; период вращения; частоту вращения?; это и есть вторая задача. Завершая экскурс в раздел кинематики «вращательное движение», перечислим его ключевые слова: угол поворота, малый промежуток времени, угловая скорость, центростремительное ускорение, период вращения, частота вращения.
Динамика Ньютона
Энергия Основная задача механики – нахождение движения тела по заданным силам. Найти движение – это значит суметь указать, в каком месте пространства, и в какой момент времени находится движущееся тело. Чтобы справиться с такой задачей, нужно располагать исчерпывающими сведениями о действующих силах. Силы должны быть известны для любой точки и любого места нахождения этого тела. Если силы известны, уравнения Ньютона позволяют определить ускорение движущегося тела. Однако при помощи одних только уравнений движения Ньютона сведения о траектории, скорости, знании момента времени, которому соответствует прохождение через данную точку пространства, не могут быть получены. Чтобы прописать движение, надо знать для любого момента времени место, где находилось тело, а также его скорость как по величине, так и по направлению. Эти данные (х, Итак, механическое состояние тела само по себе измениться не может, необходимо действие со стороны других тел; наличие силы. Будем рассуждать так. Пусть под действием силы происходит изменение механического состояния тела. Тогда должна быть физическая величина, являющаяся мерой изменения этого состояния, которая зависит как от величины силы Работа является скалярной величиной; имеет только численное значение. Вместе с тем это величина алгебраическая: если cosa> 0, работа положительна; если cosa< 0, работа отрицательна. При a = p/2 работа равна нулю. Это обстоятельство особенно отчётливо показывает, что понятие работы в механике существенно отличается от обыденного представления о работе. Найдём работу, совершаемую при растяжении или сжатии пружины, рис. 2.6.. Чтобы выполнялся закон Гука
В приведённом примере результатом совершённой работы является изменение механического состояния, которое определяется лишь координатой х; геометрическая сумма сил равна нулю, движение равномерное и прямолинейное. Рассмотрим пример, в котором совершённая работа по изменению механического состояния, может быть выражена через изменение скорости (D Въедливому читателю преобразования проделать самостоятельно. Итак, приведённые примеры показали, когда есть взаимодействие тел, сопровождающееся изменением механического состояния, совершается работа. Совершённая работа равна разности некоей физической величины, содержащей параметры начального и конечного механических состояний. Физическая величина обязательно является функцией состояния – положения тел х и скорости движения На практике большое значение имеет не только величина совершённой работы, но и время, в течение которого она совершается. Поэтому для характеристики механизмов, предназначенных для совершения работы, вводится понятие мощности. Новая величина, равная отношению работы к промежутку времени, за которое эта работа совершается Завершая экскурс в раздел динамики «Понятие механического состояния. Работа. Мощность. Энергия», перечислим его ключевые слова: механическое состояние, механическая работа, мощность, энергия потенциальная и кинетическая, закон сохранения энергии.
Квазиупругая сила В предыдущем параграфе было установлено, несмотря на большое разнообразие колебательных процессов, как по физической природе, так и по степени сложности, все они совершаются по общим закономерностям и могут быть сведены к простейшим, гармоническим колебаниям, совершаемым по закону х(t) = Следует ожидать, скорость тела, как и смещение, должна изменяться по гармоническому закону. Взяв производную от смещения х по времени, находим Уравнение скорости функционально зависит от времени, следовательно, колебательное движение совершается с ускорением. Ускорение можно найти, продифференцировав уравнение скорости по времени:
Графически уравнение ускорения представлено на рис. 3.3. мелким пунктиром. Если учесть, Сравнение формул смещения, скорости и ускорения приводит к следующим выводам: изменение этих физических величин совершается по закону синуса или косинуса с одинаковой циклической частотой или периодом В заключение следует обратить внимание на то, что по второму закону динамики сила, действующая на тело, совершающее колебательный процесс, запишется: F = ma = –m× Капиллярные явления В параграфе 4.1., рис. 4.2. мы выяснили (посмотрели? ), в приповерхностном слое жидкости на молекулу действует равнодействующая сил
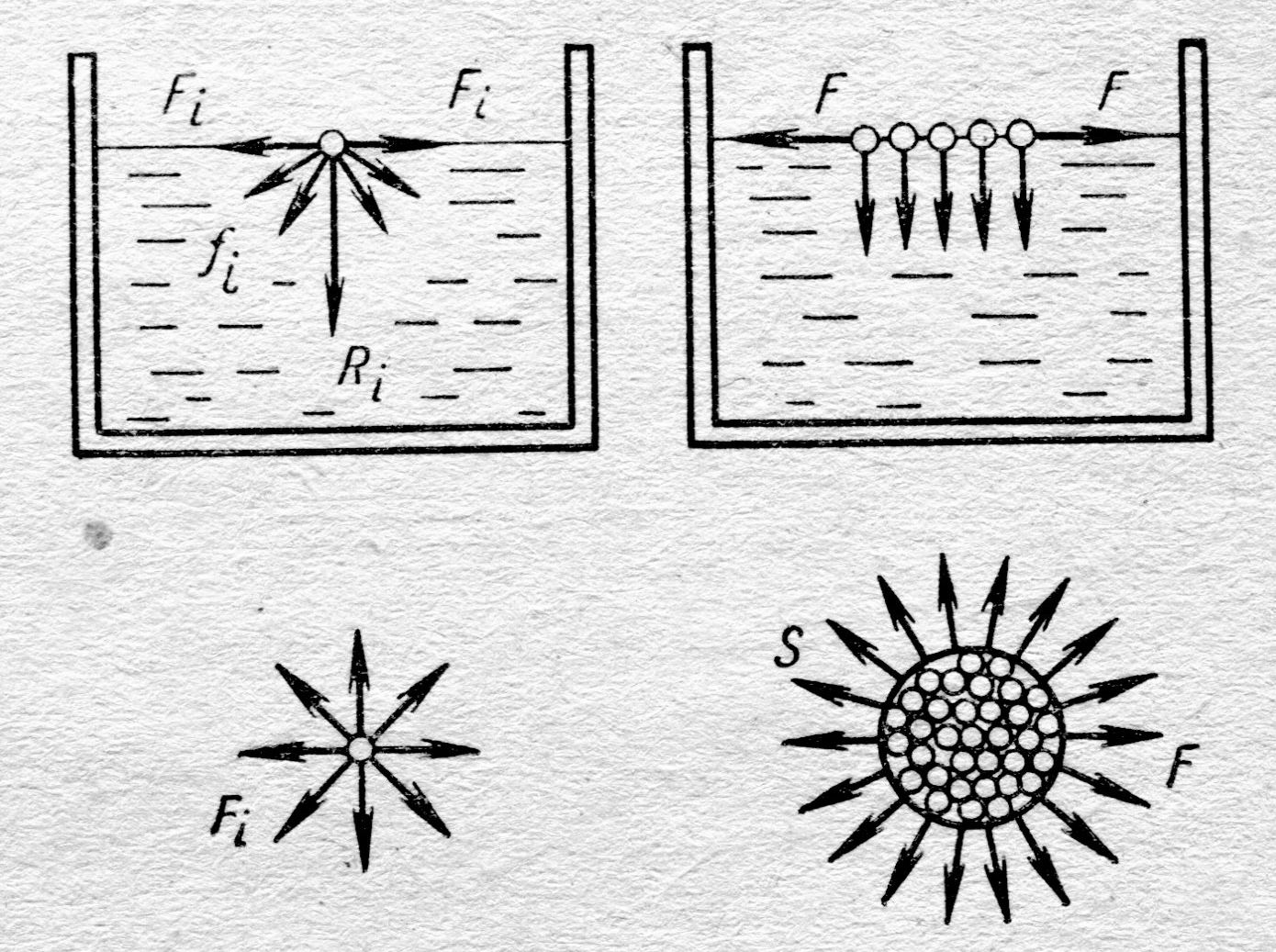 Кроме того, на молекулы поверхностного слоя действуют силы Кроме того, на молекулы поверхностного слоя действуют силы 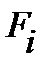 , лежащие в плоскости, касательной к поверхности жидкости (см. рис. 4.8., справа). Эти внешние силы F, растягивающие плёнку, и называют силами поверхностного натяжения. Если выделить на поверхности жидкости площадку S, рис. 4.8., справа (внизу), то силы F, направленные наружу, являются внешними силами; они перпендикулярны периметру площадки S и касательные к поверхности жидкости. Для всех молекул, лежащих внутри площадки S, все эти силы , лежащие в плоскости, касательной к поверхности жидкости (см. рис. 4.8., справа). Эти внешние силы F, растягивающие плёнку, и называют силами поверхностного натяжения. Если выделить на поверхности жидкости площадку S, рис. 4.8., справа (внизу), то силы F, направленные наружу, являются внешними силами; они перпендикулярны периметру площадки S и касательные к поверхности жидкости. Для всех молекул, лежащих внутри площадки S, все эти силы 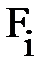 взаимно уравновешиваются. взаимно уравновешиваются.
Всё сказанное об особых условиях, в которых находятся молекулы поверхностного слоя жидкости, в целом относится и к твёрдым телам. Следовательно, твёрдые тела, как и жидкости, обладают поверхностным натяжением. Следует ожидать, если жидкость имеет границу с твёрдым телом, то эта система, с учётом сил межмолекулярного взаимодействия, принимает конфигурацию, соответствующую минимуму суммарной потенциальной энергии; поверхностной, с учётом и поля сил тяжести. В частности, это проявляется на искривлении поверхности жидкости; явление смачивания (не смачивания, например, ртуть). Под искривлённой поверхностью жидкости помимо внутреннего давления силы поверхностного натяжения создают дополнительное давление на жидкость. Оно прибавляется к давлению, созданному поверхностным слоем, или вычитается из него. Кстати, давление, создаваемое поверхностным слоем воды ~ 1, 7× 109 Па, что значительно превышает давление атмосферы; поэтому все жидкости уже сильно сжаты внутренними молекулярными силами. Чтобы вызвать дополнительное уменьшение их объёма, сжать, требуется приложить очень большое внешнее давление. (Вспомните неудачные прыжки в воду в детские годы; «нежная» при умывании вода, больно жалит при взаимодействии с нею за малый промежуток времени.)
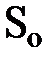 ; радиус основания ; радиус основания  (см. рис. 4.9.). Силы поверхностного натяжения (см. рис. 4.9.). Силы поверхностного натяжения 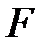 , действующие по периметру площадки S (рис. 4.9.), создают равнодействующую , действующие по периметру площадки S (рис. 4.9.), создают равнодействующую 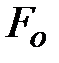 , перпендикулярную основанию , перпендикулярную основанию 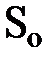 и равную и равную  . Составляющие . Составляющие 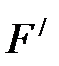 силы поверхностного натяжения силы поверхностного натяжения 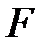 в сумме дают нуль (почему? Нарисуйте вид сверху, поможет). Учитывая, что давление равно силе приходящейся на единицу площади, т.е., в сумме дают нуль (почему? Нарисуйте вид сверху, поможет). Учитывая, что давление равно силе приходящейся на единицу площади, т.е., 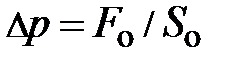 , для дополнительного давления на жидкость от сил поверхностного натяжения, обусловленного кривизной поверхности, получим аналитическое выражение , для дополнительного давления на жидкость от сил поверхностного натяжения, обусловленного кривизной поверхности, получим аналитическое выражение 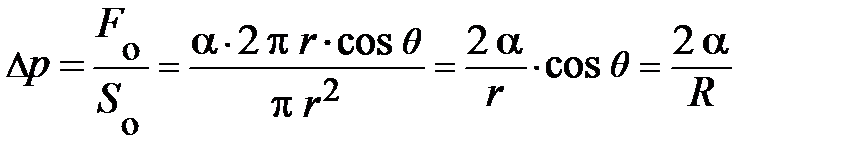 . .
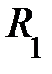 и максимальный и максимальный  ; они лежат во взаимно перпендикулярных плоскостях и называются главными радиусами кривизны поверхности S в данной её точке (рис. 4.10.). Точное выражение для дополнительного давления под искривлённой поверхностью жидкости любой формы вывел французский математик и физик Лаплас в 1805 году. Оно может быть представлено в виде ; они лежат во взаимно перпендикулярных плоскостях и называются главными радиусами кривизны поверхности S в данной её точке (рис. 4.10.). Точное выражение для дополнительного давления под искривлённой поверхностью жидкости любой формы вывел французский математик и физик Лаплас в 1805 году. Оно может быть представлено в виде  . Знак плюс соответствует выпуклой поверхности, знак минус – вогнутой поверхности; . Знак плюс соответствует выпуклой поверхности, знак минус – вогнутой поверхности; 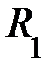 и и  здесь алгебраические величины – если центр кривизны находится под данной поверхностью, радиус кривизны положительный; если центр кривизны лежит над поверхностью, радиус кривизны отрицателен (отобразите на рис; сделали? ). здесь алгебраические величины – если центр кривизны находится под данной поверхностью, радиус кривизны положительный; если центр кривизны лежит над поверхностью, радиус кривизны отрицателен (отобразите на рис; сделали? ).
Если силы сцепления между молекулами жидкости больше, чем между молекулами жидкости и твёрдого тела, то жидкость, искривляясь, стремится уменьшить границу соприкосновения с твёрдым телом, т.е. сжимается, «опускается» по стенкам (рис. 4.11., справа); в этом и состоит суть явления несмачивания. Изогнутую поверхность принято называть мениском, а узкую трубку (щель и т.п.) – капилляром. При большой кривизне мениска внутреннее давление жидкости в капилляре (на уровне горизонта поверхности) будет меньше, чем вне капилляра, на величину избыточного давления под искривлённой (сферической) поверхностью. По закону Паскаля это должно сопровождаться выдавливанием вверх жидкости в капилляре (при смачивании, рис. 4.11., слева). Жидкость в капилляре поднимается до тех пор, пока давление столба жидкости не скомпенсирует уменьшение давления, обусловленное искривлением поверхности жидкости; давление столба жидкости должно равняться капиллярному давлению. Аналитически это запишется Dр = Завершая экскурс в раздел «Элементы механики сплошных сред: жидкости и газы», перечислим его ключевые понятия: квазикристаллическая структура, сфера молекулярного действия, молекулярное давление, макроскопический элемент, гидростатическое давление (объёмные силы), уравнение неразрывности потока, трубка тока, идеальная несжимаемая жидкость, искривлённая поверхность, капиллярное (лапласовское) давление.
Методы исследования
Закон парциальных давлений. Несмотря на простоту вывода основного уравнения молекулярно-кинетической теории газов, формулу Пока будем обходиться понятием эмпирической температуры, т.е. той физической величины, которая измеряется на опыте и связана с интуитивным представлением о тепловом равновесии. Эмпирическая температура объекта – это то, что измеряется другим объектом-термометром, приведённым в состояние теплового равновесия с исходным объектом, и служит характеристикой равновесного состояния. В роли такого объекта-термометра может служить любой объект в состоянии теплового равновесия, характеристики которого реагируют на изменение этого состояния. Популярное:
|
Последнее изменение этой страницы: 2017-03-11; Просмотров: 567; Нарушение авторского права страницы