Понятие механического состояния. Работа. Мощность.

Энергия

Основная задача механики – нахождение движения тела по заданным силам. Найти движение – это значит суметь указать, в каком месте пространства, и в какой момент времени находится движущееся тело. Чтобы справиться с такой задачей, нужно располагать исчерпывающими сведениями о действующих силах. Силы должны быть известны для любой точки и любого места нахождения этого тела. Если силы известны, уравнения Ньютона позволяют определить ускорение движущегося тела. Однако при помощи одних только уравнений движения Ньютона сведения о траектории, скорости, знании момента времени, которому соответствует прохождение через данную точку пространства, не могут быть получены. Чтобы прописать движение, надо знать для любого момента времени место, где находилось тело, а также его скорость как по величине, так и по направлению. Эти данные (х, 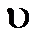) однозначно характеризуют «механическое состояние» движущегося тела.

Итак, механическое состояние тела само по себе измениться не может, необходимо действие со стороны других тел; наличие силы. Будем рассуждать так. Пусть под действием силы происходит изменение механического состояния тела. Тогда должна быть физическая величина, являющаяся мерой изменения этого состояния, которая зависит как от величины силы , так и от изменения положения (координаты х или перемещения DS). Естественно, чем больше сила и перемещение, тем больше изменение механического состояния. Поэтому было введено понятие «механическая работа». Количественной характеристикой работы, а, следовательно, и мерой изменения механического состояния, является произведение силы, действующей на тело в направлении движения, на пройденный телом путь: А = = F× DS. Если направление силы не совпадает с направлением перемещения, аналитическое выражение работы примет вид: А = F× DS× cosa. Здесь a – угол между направлением силы и перемещением. Практический опыт человечества это подтверждает. Хорошим примером является золотое правило механики: выигрывая в силе, проигрываем в расстоянии.

Работа является скалярной величиной; имеет только численное значение. Вместе с тем это величина алгебраическая: если cosa> 0, работа положительна; если cosa< 0, работа отрицательна. При a = p/2 работа равна нулю. Это обстоятельство особенно отчётливо показывает, что понятие работы в механике существенно отличается от обыденного представления о работе.

Найдём работу, совершаемую при растяжении или сжатии пружины, рис. 2.6.. Чтобы выполнялся закон Гука ; растяжение, сжатие будем производить медленно. В выражение работы следует подставить среднее значение силы , то есть (почему? ). После преобразований аналитическое выражение работы по растяжению, сжатию пружины как по величине, так и по знаку одинаково и примет вид: ; желательно проделать преобразования самостоятельно. Здесь учтено, в момент начала сжатия х₁ =

Рис. 2.6.

0, (см. рис. 2.6.), а х₂ = х. Однако работа упругой силы, силы, действующей стороны пружины на деформирующее её тело, и при растяжении и при сжатии равна –kх²/2; желательно убедиться аналитически.

В приведённом примере результатом совершённой работы является изменение механического состояния, которое определяется лишь координатой х; геометрическая сумма сил равна нулю, движение равномерное и прямолинейное. Рассмотрим пример, в котором совершённая работа по изменению механического состояния, может быть выражена через изменение скорости (D 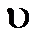); движение равноускоренное, рис. 2.7., сила > 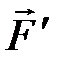. По второму закону динамики равнодействующая сил = 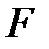– 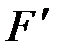= m× a и под действием её совершается работа А = × DS= = m× a× DS, где а – среднее ускорение на участке пути DS, равное а = D 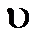/Dt. Подставляя ускорение в формулу работы, получаем уравнение вида: А = = m× D 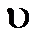× DS/Dt, где DS/Dt = 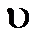– средняя скорость на участке пути DS и тогда аналитическое выражение работы принимает вид: А = m× D 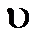× 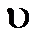. Учитывая, что и 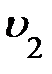мгновенные скорости в начале и в конце пути DS, изменение скорости D 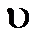= 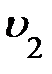– , а средняя скорость на этом участке 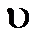= ( 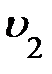+ )/2, и тогда конечное выражение для работы принимает вид: А = .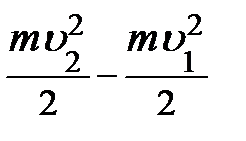

Въедливому читателю преобразования проделать самостоятельно.

Итак, приведённые примеры показали, когда есть взаимодействие тел, сопровождающееся изменением механического состояния, совершается работа. Совершённая работа равна разности некоей физической величины, содержащей параметры начального и конечного механических состояний. Физическая величина обязательно является функцией состояния – положения тел х и скорости движения 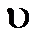. Эта физическая величина характеризует работоспособность системы взаимодействующих тел, а её разность начального и конечного состояний – количественная мера совершённой механической работы. Физическую величину назвали механической энергией; обозначают её, как правило, буквой Е = f(x, 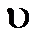) и она является функцией параметров механического состояния. Энергию, определяемую скоростью движения, принято называть кинетической К = m 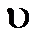²/2; энергия, определяемая взаимным расположением тел, называется потенциальной П = kх²/2 и её вид тесно связан с характером силового поля (например, гравитационного, электрического…). Полная механическая энергия определяется суммой энергий, потенциальной и кинетической Е = К + П.

На практике большое значение имеет не только величина совершённой работы, но и время, в течение которого она совершается. Поэтому для характеристики механизмов, предназначенных для совершения работы, вводится понятие мощности. Новая величина, равная отношению работы к промежутку времени, за которое эта работа совершается , показывает, какую работу данное устройство может совершить за единицу времени. Поскольку DА = F× DS, а DS/Dt равно средней скорости на пути DS, то среднее значение мощности за время Dt равно N = F× 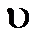и является величиной скалярной. Единицей измерения мощности является Вт (Дж/с); это значит, что за каждую секунду механизм совершает работу в один Дж.

Завершая экскурс в раздел динамики «Понятие механического состояния. Работа. Мощность. Энергия», перечислим его ключевые слова: механическое состояние, механическая работа, мощность, энергия потенциальная и кинетическая, закон сохранения энергии.

⇐ Предыдущая 1 2 3 4 567 8 9 10 Следующая ⇒