
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Связь параметров колебательной системы с периодом колебаний. Энергия колебательной системы с одной степенью свободы
В предыдущих параграфах данной главы были введён параметр колебательной системы w – круговая или циклическая частота и частота колебаний n, связанные между собой соотношением Периодом колебаний называют промежуток времени, по истечении которого колебание повторяется, то есть колеблющаяся точка, тело проходит те же положения и в том же направлении (см. рис. 3.2.). Аналитически это может быть записано так х(t + n× Т) = х(t); здесь n – целое число (периодов), Т – период колебаний, t – промежуток времени, через который нас интересует положение движущейся точки, тела. Аналитическая запись может быть прочитана так, через произвольное целое число периодов тело будет двигаться так же, как и в данный момент времени. Уравнение движения примет вид: Подводя итог сказанному выше, обратим внимание на следующее. Всякое колебательное движение есть движение, происходящее с ускорением, поэтому на колеблющееся тело должна действовать сила, сообщающая это ускорение. Направление силы совпадает с направлением ускорения, а вектор ускорения при гармоническом колебании всегда направлен к положению равновесия
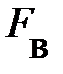 ; она направлена по касательной к траектории движения. При малых углах отклонения от положения равновесия, синус угла a равен его радианной мере и синус угла a запишется ; она направлена по касательной к траектории движения. При малых углах отклонения от положения равновесия, синус угла a равен его радианной мере и синус угла a запишется 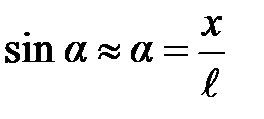 , а формула возвращающей силы F = = mg× sina примет вид F @ mg× , а формула возвращающей силы F = = mg× sina примет вид F @ mg× 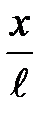 . Во втором законе Ньютона последствия возвращающей силы равны произведению массы тела на ускорение колебательного движения. Формула возвращающей силы немедленно принимает вид mg× . Во втором законе Ньютона последствия возвращающей силы равны произведению массы тела на ускорение колебательного движения. Формула возвращающей силы немедленно принимает вид mg× 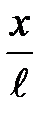 = m× = m× 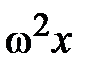 . Проведя в последнем равенстве несложные преобразования, читатель самостоятельно может получить аналитическое выражение для периода колебаний математического маятника . Проведя в последнем равенстве несложные преобразования, читатель самостоятельно может получить аналитическое выражение для периода колебаний математического маятника 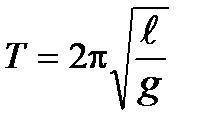 . Из формулы следует, параметрами колебательной системы являются длина нити и ускорение свободного падения. В системах такого рода длина нити характеризует инертные свойства маятника (математического, физического) к движению, а именно, к отклонению из состояния равновесия. Ускорение свободного падения в таких системах определяет возвращающее действие в состояние равновесия. . Из формулы следует, параметрами колебательной системы являются длина нити и ускорение свободного падения. В системах такого рода длина нити характеризует инертные свойства маятника (математического, физического) к движению, а именно, к отклонению из состояния равновесия. Ускорение свободного падения в таких системах определяет возвращающее действие в состояние равновесия.Таким образом, простейшая колебательная система, состоящая из двух тел, является замкнутой консервативной системой, в которой действуют только внутренние силы. Это указывает на то, что работа внутренних сил определяется изменением потенциальной энергии системы и равна изменению кинетической энергии; то есть колебательные движения в механических системах сопровождаются периодическими превращениями кинетической энергии колеблющихся тел в потенциальную энергию взаимодействия частей системы и обратно. Запишем потенциальную энергию системы:
3.4. Понятие сплошной среды. Колебания в сплошных средах. Понятие волны. Основные определения. Уравнение волны. Предыдущие параграфы курса физики были посвящены анализу природы на основе простейшей модели вещества – модели частицы. Это позволило установить многие, хорошо уже известные фундаментальные законы действительности и описать движение в системе частица – внешнее воздействие. В частности, это относится к рассмотренным колебательным системам. Главным инструментом анализа в такой системе служила возможность представить её в виде совокупности независимых «частицеподобных объектов – квазичастиц». При этом «квазичастицы» делятся на две качественно различные группы – индивидуальные (например, колеблющееся тело) и существенно коллективные (поле тяготения Земли). В поле центральных сил и для систем с малым числом частиц это различие практически ни на чём не сказывается. Ситуация меняется при переходе к макроскопическим объектам, содержащим число частиц N ~ Nа, т.е. N> > 1 (здесь Nа – число Авогадро). Такой объект в условиях теплового равновесия и вблизи него ещё можно свести к рассмотрению одной «квазичастицы» индивидуального типа. Почему? Это возможно, поскольку индивидуальные «квазичастицы» ещё сохраняют внешние признаки реальных частиц; например, масса, положение, скорость частицы. Переходя к писанию колебательных процессов в сплошных (континуальных) средах, могут возникнуть трудности. В частности, характеризовать состояние сплошной (континуальной) среды через параметры состояния частицы громоздко (N> > 1), не говоря о других его характеристиках; например, скорость распространения колебания, фронт волны. При интенсивном взаимодействии частиц в макроскопическом объекте их описание возможно лишь на основе «квазичастиц» существенно коллективного типа. Поскольку при громадном числе частиц (N> > 1), входящих в макроскопический объект, подобные «квазичастицы» не обладают внешними признаками реальных частиц. В частности, они «размазаны» по конечному объёму DV и модель частицы или корпускулы к ним не применима. Ещё большие трудности возрастают, если учесть, что частицы в макроскопическом объекте движутся хаотически, а задать точное состояние каждой частицы невозможно. Естественно, описание подобных объектов лучше осуществлять в идеализированной модели вещества – модели сплошной среды. Интуитивное представление о такой модели мы получаем из повседневной жизни, наблюдая, например, за однородной жидкостью или воспринимая звуки из окружающей реальности. При этом нам кажется, что частицы вещества расположены столь тесно, что дискретная структура его не проявляется. Таким образом, модель сплошной среды – континуума существенно отличается от модели корпускулы. Универсальность этой модели в том, что любые материальные объекты с большим числом частиц N> > 1 – жидкие, газообразные, твёрдые могут трактоваться как сплошная среда, Этот бесконечно большой ансамбль мельчайших частиц, соответствующим образом организованный в каждой из указанных сред, находится в состоянии непрекращающегося беспорядочного теплового движения. В отличие от твёрдых жидкие и газообразные среды характерны тем, что не оказывают сопротивления сдвигу и поэтому изменяют свою форму под воздействием сколь угодно малых сил. Для изменения же объёма указанных сред требуются внешние силы, что позволяет утверждать – в жидкостях, газах и твёрдых телах возникают упругие силы. Степень упругости определяется взаимодействием между частицами, образующими среду. Наш жизненный опыт этим утверждениям не противоречит. Появление упругих сил в рассматриваемых средах обусловлено изменением равновесного состояния, которое сложилось в среде. Выше уже упоминалось, условием устойчивого состояния системы является минимальное значение её энергии в данных условиях. Естественно ожидать, при образовании сплошных сред (твёрдых тел) наряду с силами отталкивания между атомами (ионами), должны существовать силы притяжения. При нарушении равновесия будут возникать, соответственно, те или иные силы; в сплошной среде распространяется упругая деформация (продольная, поперечная). Перейдём к установлению характеристик сплошной среды, определяющих её состояние и движение; в частности, на примере колебательного движения. Покажем их качественное отличие от аналогичных характеристик частицы. В макроскопических объектах входящие в них частицы могут участвовать лишь в хаотических относительных движениях. В этих условиях выглядит довольно загадочно тот факт, что в этих объектах всё-таки возникают волнообразные движения, наблюдаемые на опыте; к такого рода движениям относятся звук или волны на поверхности жидкости. Однако, учитывая тот факт, что механическое действие в сплошных средах передаётся с конечной скоростью, то деформация в упругой (сплошной) среде передаётся последовательно от одной точки среды (тела) к соседней точке. Если среда испытала сжимающее действие, – на поверхность жидкости упало тело, по твёрдому телу нанесён удар предметом, произошло резкое сжатие воздуха – то образуется уплотнение среды, которое распространяется с определённой скоростью Остаётся осознать, почему подобные движения в сплошной среде в целом оказываются упорядоченными, несмотря на то, что атомы (молекулы) в ней движутся хаотически. Причина, по-видимому, здесь кроется в том, что положение и движение каждого элемента сплошной среды DV определяется её соседними элементами. Эти элементы не могут двигаться независимо и хаотически, поскольку в противном случае в среде должны были бы образоваться разрывы. Наблюдая за поведением волн на поверхности воды, общаясь через звуковые сигналы в сплошной среде – воздух мы этого не обнаруживаем. Таким образом, если элемент среды выполняет какое-то движение, то соседние с ним элементы также должны выполнять подобные движения; то есть движения всех элементов среды должны быть согласованными. Хаотическое же движение множества атомов в каждом элементе среды проявляется только в том, что выделяемый элемент среды действует на соседние элементы с некоторой средней силой; которая обусловлена воздействием всей совокупности атомов в нём. Такого рода силу принято называть поверхностной. Если провести аналогию, то атомы в элементе сплошной среды напоминают «рой мошек», воздействующих на стенки сосуда, центр масс которого совершает какое-либо упорядоченное движение. Таким образом, переход от рассмотрения «частиц» – атомов к «квазичастицам» – элементам среды, содержащим N> > DN> > 1 атомов, позволил выявить – элементы среды испытывают воздействие со стороны отдельных атомов, входящих в соседние элементы. Суммарный результат этого воздействия можно характеризовать средней силой, величина которой тем больше, чем больше площадь поверхности DS, окружающей элемент среды. Особенности поверхностных сил, в частности, их направления различны для твёрдых, жидких и газообразных сред. Однако все поверхностные силы могут быть разделены на силы упругости и силы вязкости. Их подробному рассмотрению будет уделено внимание в соответствующих разделах основного курса физики.
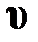 , – перейдём к аналитическому описанию волнового процесса. Пусть некая область упругой среды (рис. 3.5.), находящаяся в начале отсчёта (направление удара), колеблется согласно уравнению , – перейдём к аналитическому описанию волнового процесса. Пусть некая область упругой среды (рис. 3.5.), находящаяся в начале отсчёта (направление удара), колеблется согласно уравнению 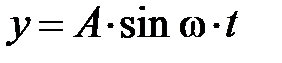 ; здесь А – амплитуда колебания, ; здесь А – амплитуда колебания, 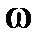 – циклическая частота колебания в среде, начальную фазу jо – примем равной нулю, t – время. Запишем уравнение колебания точки, расположенной вдоль линии распространения упругой деформации на расстоянии х от начальной точки (удара, рис. 3.5.). Мы не можем записать его в том же виде, так как эта точка начинает колебание с запозданием на время – циклическая частота колебания в среде, начальную фазу jо – примем равной нулю, t – время. Запишем уравнение колебания точки, расположенной вдоль линии распространения упругой деформации на расстоянии х от начальной точки (удара, рис. 3.5.). Мы не можем записать его в том же виде, так как эта точка начинает колебание с запозданием на время 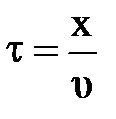 , нужное для распространения деформации на расстояние х. Поэтому колебание в точке х должно быть сдвинуто по фазе по отношению к начальной точке (точке удара). Точка х будет находиться в момент времени t в той же фазе колебания, в какой находилась начальная точка в момент времени на , нужное для распространения деформации на расстояние х. Поэтому колебание в точке х должно быть сдвинуто по фазе по отношению к начальной точке (точке удара). Точка х будет находиться в момент времени t в той же фазе колебания, в какой находилась начальная точка в момент времени на 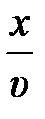 более ранний. Следовательно, уравнение колебания точки, сдвинутой на расстояние х от начала координат, имеет вид более ранний. Следовательно, уравнение колебания точки, сдвинутой на расстояние х от начала координат, имеет вид 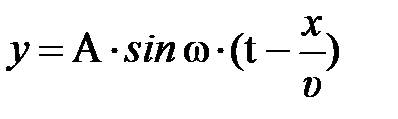 , здесь , здесь 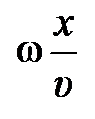 – сдвиг по фазе колебания в точке х по отношению к началу отсчёта. – сдвиг по фазе колебания в точке х по отношению к началу отсчёта.
Написанное уравнение называют уравнением волны, оно охватывает колебания всех точек упругой среды, расположенных на любых расстояниях по отношению к начальной точке. В действительности, как мы знаем, колеблются не точки, расположенные вдоль выбранного направления, а совокупность точек (частиц DN), заключённых в некотором объёме DV. Распространяясь от источника колебаний, волновой процесс охватывает всё новые и новые части пространства. Геометрическое место точек, до которых доходят колебания к моменту времени t, называется фронтом волны (волновым фронтом). Фронт волны представляет собой ту поверхность, которая отделает часть пространства уже вовлечённую в волновой процесс, от области, в которой колебания ещё не возникали. Геометрическое место точек, колеблющихся в одной фазе, называется волновой поверхностью. Волновую поверхность можно провести через любую точку пространства, охваченного волновым процессом. Следовательно, волновых поверхностей существует бесконечное множество, в то время как волновой фронт в каждый момент времени только один. Если волновые поверхности остаются неподвижными (они проходят через положения равновесия частиц, колеблющихся в одной фазе), то волновой фронт всё время перемещается.
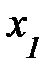 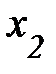 Поскольку волна представляет собой повторяющееся в среде упругое колебание, например, поперечное (рис. 3.6. и 3.5.а), определим её пространственный период; расстояние, через которое повторяется волнообразное распределение в среде (рис. 3.6.); можно вспомнить волны на поверхности воды, если на неё упал предмет. Запишем уравнение волны для промежутка времени, кратного числу периодов. Пусть максимальное отклонение у от положения равновесия для первого горба (рис. 3.6.) произошло в момент времени t = T× n, а для второго через время t = T× (n+1). Уравнения волны для этих точек упругой среды примут вид: Поскольку волна представляет собой повторяющееся в среде упругое колебание, например, поперечное (рис. 3.6. и 3.5.а), определим её пространственный период; расстояние, через которое повторяется волнообразное распределение в среде (рис. 3.6.); можно вспомнить волны на поверхности воды, если на неё упал предмет. Запишем уравнение волны для промежутка времени, кратного числу периодов. Пусть максимальное отклонение у от положения равновесия для первого горба (рис. 3.6.) произошло в момент времени t = T× n, а для второго через время t = T× (n+1). Уравнения волны для этих точек упругой среды примут вид:
Если пренебречь трением и тепловыми потерями при распространении колебаний в среде, амплитуда колебаний у, по мере распространения волны, в точках Завершая экскурс в раздел механики «Гармонические колебания. Волновые процессы», перечислим его ключевые понятия: «потенциальная яма», уравнение колебания, квазиупругая сила, параметры колебательной системы, сплошная среда, квазичастицы сплошной среды, уравнение волны, фронт волны, волновая (фазовая) поверхность.
Популярное:
|
Последнее изменение этой страницы: 2017-03-11; Просмотров: 839; Нарушение авторского права страницы