Ускорение при криволинейном движении (тангенциальное и нормальное ускорение).
Если траектория движения материальной точки представляет собой кривую линию, то такое движение мы будем называть криволинейным.
При таком движении 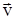 изменяется как по величине, так и по направлению. Следовательно, при криволинейном движении
изменяется как по величине, так и по направлению. Следовательно, при криволинейном движении  .
.
 Рассмотрим движение материальной точки по криволинейной траектории (рис. 2.11). Вектор скорости движения в любой точке траектории направлен по касательной к ней. Пусть в точке M0 скорость
Рассмотрим движение материальной точки по криволинейной траектории (рис. 2.11). Вектор скорости движения в любой точке траектории направлен по касательной к ней. Пусть в точке M0 скорость 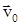 , а в точке М –
, а в точке М – 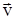 . При этом считаем, что промежуток времени Dt при переходе из точки М0 в точку М настолько мал, что изменением ускорения по величине и направлению можно пренебречь.
. При этом считаем, что промежуток времени Dt при переходе из точки М0 в точку М настолько мал, что изменением ускорения по величине и направлению можно пренебречь.
 Вектор изменения скорости
Вектор изменения скорости  . (В данном случае разность 2х векторов
. (В данном случае разность 2х векторов 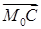 и
и 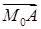 будет равна
будет равна  ). Разложим вектор
). Разложим вектор 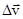 , который характеризует изменение скорости как по величине, так и по направлению на две составляющие
, который характеризует изменение скорости как по величине, так и по направлению на две составляющие  и
и  . Составляющая
. Составляющая  , которая является касательной к траектории в точке М0, характеризует изменение скорости по величине за время Dt, в течение которого была пройдена дуга М0М и называется тангенциальной составляющей вектора изменения скорости (
, которая является касательной к траектории в точке М0, характеризует изменение скорости по величине за время Dt, в течение которого была пройдена дуга М0М и называется тангенциальной составляющей вектора изменения скорости (  ). Вектор
). Вектор  , направленный в пределе, когда Dt ® 0, по радиусу к центру, характеризует изменение скорости по направлению и называется нормальной составляющей вектора изменения скорости (
, направленный в пределе, когда Dt ® 0, по радиусу к центру, характеризует изменение скорости по направлению и называется нормальной составляющей вектора изменения скорости ( 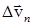 ).
).
Таким образом, вектор изменения скорости  равен сумме двух векторов
равен сумме двух векторов  .
.
Тогда можно записать, что
 .
.
При бесконечном уменьшении Dt®0 угол Da при вершине DM0АС будет стремиться к нулю. Тогда вектором 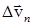 можно пренебречь по сравнению с вектором
можно пренебречь по сравнению с вектором  , а вектор
, а вектор

будет выражать тангенциальное ускорение и характеризовать быстроту изменения скорости движения по величине. Следовательно, тангенциальное ускорение численно равно производной от модуля скорости по времени  и направлено по касательной к траектории.
и направлено по касательной к траектории.
Вычислим теперь вектор 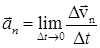 , называемый нормальным ускорением. При достаточно малом Dt участок криволинейной траектории можно считать частью окружности. В этом случае радиусы кривизны M0O и MO будут равны между собой и равны радиусу окружности R.
, называемый нормальным ускорением. При достаточно малом Dt участок криволинейной траектории можно считать частью окружности. В этом случае радиусы кривизны M0O и MO будут равны между собой и равны радиусу окружности R.
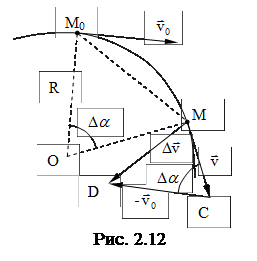
Повторим рисунок. Ð М0ОМ = Ð МСD, как углы со взаимно перпендикулярными сторонами (рис. 2. 12). При малом Dt можно считать |v0|=|v|, поэтому DМ0ОМ = DМDC подобны как равнобедренные треугольники с одинаковыми углами при вершине.
Поэтому из рис. 2.11 следует
 Þ
Þ  ,
,
но DS = vср.× Dt, тогда 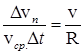 .
.
Переходя к пределу при Dt ® 0 и учитывая, что при этом vср. = v находим
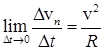 , т.е.
, т.е. 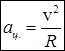 (2.5)
(2.5)
 Т.к. при Dt ® 0 угол Da ® 0, то направление этого ускорения совпадает с направлением радиуса R кривизны или с направлением нормали к скорости
Т.к. при Dt ® 0 угол Da ® 0, то направление этого ускорения совпадает с направлением радиуса R кривизны или с направлением нормали к скорости 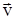 , т.е. вектор
, т.е. вектор  . Поэтому это ускорение часто называют центростремительным. Оно характеризует быстроту изменения скорости движения по направлению.
. Поэтому это ускорение часто называют центростремительным. Оно характеризует быстроту изменения скорости движения по направлению.
Полное ускорение определяется векторной суммой тангенциального и нормального ускорений  (рис. 2.13). Т.к. вектора этих ускорений взаимно перпендикулярны
(рис. 2.13). Т.к. вектора этих ускорений взаимно перпендикулярны  , то модуль полного ускорения равен
, то модуль полного ускорения равен 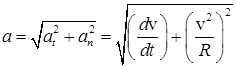 ; Направление полного ускорения определяется углом j между векторами
; Направление полного ускорения определяется углом j между векторами 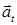 и
и 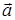 :
: 
Кинематика вращательного движения.
Угловая скорость.
ОПРЕДЕЛЕНИЕ: Вращательным движением будем называть такое движение, при котором все точки абсолютно твердого тела описывают окружности, центры которых лежат на одной прямой, называемой осью вращения.
 В качестве координаты, определяющей положение точки при вращательном движении, берут угол, характеризующий мгновенное положение радиус-вектора, проведенного из центра вращения к рассматриваемой точке (рис. 2.14)
В качестве координаты, определяющей положение точки при вращательном движении, берут угол, характеризующий мгновенное положение радиус-вектора, проведенного из центра вращения к рассматриваемой точке (рис. 2.14)
Для характеристики вращательного движения вводится понятие угловой скорости
 .
.
Вектор  направлен вдоль оси, вокруг которой вращается тело в сторону, определяемую правилом правого винта (рис. 2.15).
направлен вдоль оси, вокруг которой вращается тело в сторону, определяемую правилом правого винта (рис. 2.15).
Модуль вектора угловой скорости равен  . Если
. Если  = const, то такое движение называется равномерным, при этом
= const, то такое движение называется равномерным, при этом 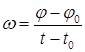 , следовательно
, следовательно  и при t0 = 0 получаем
и при t0 = 0 получаем  .
.
Если j0 = 0, то j = w·t или  .
.
Таким образом, при равномерном движении w показывает на какой угол поворачивается тело за единицу времени. Размерность угловой скорости [w]=рад/сек.
Равномерное вращение можно характеризовать периодом вращения T, под которым понимают время, за которое тело делает один полный оборот, т.е. поворачивается на угол 2p. В этом случае  , следовательно
, следовательно 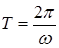 .
.
 Частота вращения (число оборотов в единицу времени): n=1/T=w/2p. Отсюда w=2pn.
Частота вращения (число оборотов в единицу времени): n=1/T=w/2p. Отсюда w=2pn.
Дополнение 1.
Поворот тела на некоторый малый угол dj можно задать в виде отрезка, длина которого равна dj, а направление совпадает с осью, вокруг которой совершен поворот. Таким образом, повороту тела можно приписать некоторое численное значение и направление. При этом направление вектора 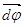 можно определить, связав его с направлением вращения тела. Такие вектора называются аксиальными или псевдовекторами, в отличие от истинных или полярных векторов, для которых направление определяется естественным образом (
можно определить, связав его с направлением вращения тела. Такие вектора называются аксиальными или псевдовекторами, в отличие от истинных или полярных векторов, для которых направление определяется естественным образом ( 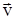 ,
, 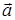 ,
, 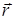 и т. д.), при операции инверсии системы координат(x → -x’, y → -y’, z → -z’) последние меняют знак на противоположный:
и т. д.), при операции инверсии системы координат(x → -x’, y → -y’, z → -z’) последние меняют знак на противоположный:  .
.
Угловое ускорение.
Вектор угловой скорости 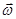 может изменяться как за счет изменения скорости вращения тела вокруг оси (в этом случае он изменяется о величине), так и за счет поворота оси вращения в пространстве (в этом случае
может изменяться как за счет изменения скорости вращения тела вокруг оси (в этом случае он изменяется о величине), так и за счет поворота оси вращения в пространстве (в этом случае 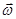 изменяется по направлению). Для характеристики быстроты изменения
изменяется по направлению). Для характеристики быстроты изменения 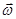 вводится физическая величина
вводится физическая величина  , называемая угловым ускорением.
, называемая угловым ускорением.
ОПРЕДЕЛЕНИЕ: Средним угловым ускорением называется величина  , где Dt – промежуток времени за который произошло изменение угловой скорости.
, где Dt – промежуток времени за который произошло изменение угловой скорости.
ОПРЕДЕЛЕНИЕ: Мгновенным ускорением  называется величина равная
называется величина равная  ;
;
Если направление оси вращения в пространстве постоянно, то угловая скорость изменяется только по величине 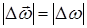 и в этом случае
и в этом случае  .
.
Если под e понимать проекцию вектора  на направление
на направление 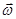 , то последняя формула примет вид
, то последняя формула примет вид  . Здесь e – алгебраическая величина и
. Здесь e – алгебраическая величина и
если w , то e> 0 (векторы 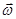 и
и  одного направления),
одного направления),
 если w ¯, то e< 0 (
если w ¯, то e< 0 (  ¯
¯ 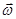 ).
).
1) Если e> 0 Þ вращение равноускоренное ( 
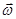 ) (рис. 2.16).
) (рис. 2.16).
2) Если e< 0 – (  ¯
¯ 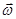 ) (рис. 2.16).
) (рис. 2.16).
В системе СИ [e]=рад/с2.
Для равноускоренного движения:
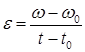
Следовательно, w = w0 + e·(t - t0). При t0 = 0 получаем w = w0 + e·t.
Тогда  ;
;
Окончательно
 (2.6)
(2.6)
Теперь установим
Популярное:
- A. Оказание помощи при различных травмах и повреждениях.
- A. особая форма восприятия и познания другого человека, основанная на формировании по отношению к нему устойчивого позитивного чувства
- B. Принципы единогласия и компенсации
- Cочетания кнопок при наборе текста
- D-технология построения чертежа. Типовые объемные тела: призма, цилиндр, конус, сфера, тор, клин. Построение тел выдавливанием и вращением. Разрезы, сечения.
- EP 3302 Экономика предприятия
- Exercise 5: Образуйте сравнительные степени прилагательных.
- H. Приглаживание волос, одергивание одежды и другие подобные жесты
- I. «Движение при закрытой автоблокировке (по путевой записке).
- I. Если глагол в главном предложении имеет форму настоящего или будущего времени, то в придаточном предложении может употребляться любое время, которое требуется по смыслу.
- I. Запоры — основная причина стресса
- I. ПРИЕМЫ ИЗМЕРЕНИЙ И СТАТИСТИЧЕСКИЕ СПОСОБЫ ОБРАБОТКИ ИХ РЕЗУЛЬТАТОВ В ПСИХОЛОГИЧЕСКОМ ИССЛЕДОВАНИИ

