РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
2.1 Постановка задачи
Пусть дана некоторая функция 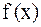 и требуется найти все или некоторые значения
и требуется найти все или некоторые значения 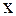 , для которых
, для которых 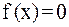 .
.
Значение 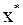 , при котором
, при котором 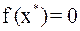 , называется корнем (или решением ) уравнения. Относительно функции
, называется корнем (или решением ) уравнения. Относительно функции 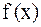 часто предполагается, что
часто предполагается, что 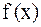 дважды непрерывно дифференцируема в окрестности корня.
дважды непрерывно дифференцируема в окрестности корня.
Корень 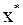 уравнения называется простым, если первая производная функции
уравнения называется простым, если первая производная функции 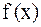 в точке
в точке 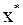 не равна нулю, т. е.
не равна нулю, т. е. 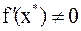 . Если же
. Если же 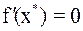 , то корень
, то корень 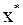 называется кратным корнем.
называется кратным корнем.
Геометрически корень уравнения есть точка пересечения графика функции 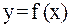 с осью абсцисс. На рис. 1 изображен график функции
с осью абсцисс. На рис. 1 изображен график функции 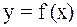 , имеющей четыре корня: два простых
, имеющей четыре корня: два простых 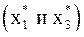 и два кратных
и два кратных 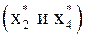 .
.
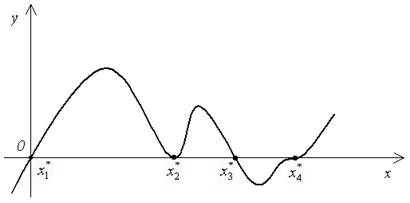
Рис. 1
Большинство методов решения уравнения ориентировано на отыскание простых корней.
2.2 Основные этапы отыскания решения
В процессе приближенного отыскания корней уравнения обычно выделяют два этапа: локализация (или отделение) корня и уточнение корня.
Локализация корня заключается в определении отрезка 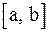 , содержащего один и только один корень. Не существует универсального алгоритма локализации корня. Иногда удобно бывает локализовать корень с помощью построения графика или таблицы значений функции
, содержащего один и только один корень. Не существует универсального алгоритма локализации корня. Иногда удобно бывает локализовать корень с помощью построения графика или таблицы значений функции 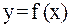 . На наличие корня на отрезке
. На наличие корня на отрезке 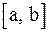 указывает различие знаков функции на концах отрезка. Основанием для этого служит следующая теорема.
указывает различие знаков функции на концах отрезка. Основанием для этого служит следующая теорема.
Теорема. Если функция 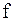 непрерывна на отрезке
непрерывна на отрезке 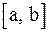 и принимает на его концах значения разных знаков так что
и принимает на его концах значения разных знаков так что 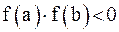 , то отрезок
, то отрезок 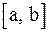 содержит по крайней мере один корень уравнения.
содержит по крайней мере один корень уравнения.
Однако корень четной кратности таким образом локализовать нельзя, так как в окрестности такого корня функция 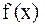 имеет постоянный знак. На этапе уточнения корня вычисляют приближенное значение корня с заданной точностью
имеет постоянный знак. На этапе уточнения корня вычисляют приближенное значение корня с заданной точностью 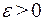 . Приближенное значение корня уточняют с помощью различных итерационных методов. Суть этих методов состоит в последовательном вычислении значений
. Приближенное значение корня уточняют с помощью различных итерационных методов. Суть этих методов состоит в последовательном вычислении значений 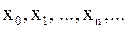 , которые являются приближениями к корню
, которые являются приближениями к корню 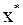 .
.
2.3 Метод половинного деления
Метод половинного является самым простым и надежным способом решения нелинейного уравнения. Пусть из предварительного анализа известно, что корень уравнения находится на отрезке 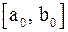 , т. е.
, т. е. 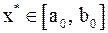 , так, что
, так, что 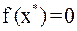 . Пусть функция
. Пусть функция 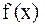 непрерывна на отрезке
непрерывна на отрезке 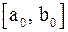 и принимает на концах отрезка значения разных знаков, т.е.
и принимает на концах отрезка значения разных знаков, т.е. 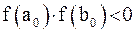 .
.
Разделим отрезок 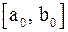 пополам. Получим точку
пополам. Получим точку 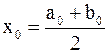 . Вычислим значение функции в этой точке:
. Вычислим значение функции в этой точке: 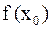 . Если
. Если 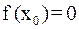 , то
, то 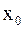 – искомый корень, и задача решена. Если
– искомый корень, и задача решена. Если 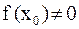 , то
, то 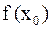 – число определённого знака:
– число определённого знака: 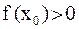 либо
либо 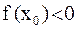 . Тогда либо на концах отрезка
. Тогда либо на концах отрезка 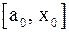 , либо на концах отрезка
, либо на концах отрезка 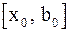 значения функции
значения функции 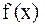 имеют разные знаки. Обозначим такой отрезок
имеют разные знаки. Обозначим такой отрезок 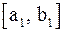 . Очевидно, что
. Очевидно, что 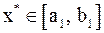 и длина отрезка
и длина отрезка 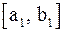 в два раза меньше, чем длина отрезка
в два раза меньше, чем длина отрезка 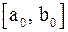 . Поступим аналогично с отрезком
. Поступим аналогично с отрезком 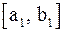 . В результате получим либо корень
. В результате получим либо корень 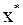 , либо новый отрезок
, либо новый отрезок 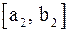 и т. д. (рис. 2).
и т. д. (рис. 2).
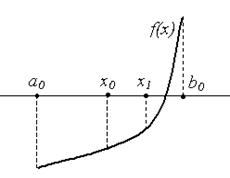
Рис. 2
Середина 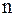 -го отрезка
-го отрезка 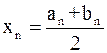 . Очевидно, что длина отрезка
. Очевидно, что длина отрезка 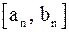 будет равна
будет равна 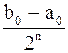 , а так как
, а так как 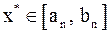 , то
, то
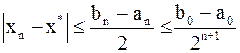 . (1)
. (1)
Критерий окончания. Из соотношения (1) следует, что при заданной точности приближения 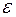 вычисления заканчиваются, когда будет выполнено неравенство
вычисления заканчиваются, когда будет выполнено неравенство 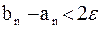 или неравенство
или неравенство 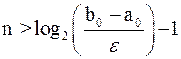 . Таким образом, количество итераций можно определить заранее. За приближенное значение корня берется величина
. Таким образом, количество итераций можно определить заранее. За приближенное значение корня берется величина 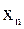 .
.
2.4 Метод простой итерации
Пусть уравнение 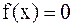 можно заменить эквивалентным ему уравнением
можно заменить эквивалентным ему уравнением
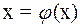 . (2)
. (2)
Выберем каким-либо образом начальное приближение 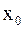 . Вычислим значение функции
. Вычислим значение функции 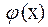 при
при 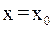 и найдем уточненное значение
и найдем уточненное значение 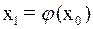 . Подставим теперь
. Подставим теперь 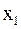 в уравнение (1) и получим новое приближение
в уравнение (1) и получим новое приближение 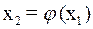 и т. д. Продолжая этот процесс неограниченно, получим последовательность приближений к корню:
и т. д. Продолжая этот процесс неограниченно, получим последовательность приближений к корню:
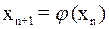 . (3)
. (3)
Формула (3) является расчетной формулой метода простой итерации.
Если последовательность 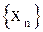 сходится при
сходится при 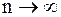 , т. е. существует
, т. е. существует
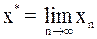 (4)
(4)
и функция 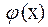 непрерывна, то, переходя к пределу в (3) и учитывая (4), получим:
непрерывна, то, переходя к пределу в (3) и учитывая (4), получим: 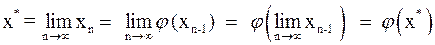 .
.
Таким образом, 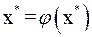 , следовательно,
, следовательно, 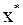 – корень уравнения (2).
– корень уравнения (2).
Сходимость метода. Сходимость метода простой итерации устанавливает следующая теорема.
Теорема. Пусть функция 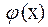 определена и дифференцируема на отрезке
определена и дифференцируема на отрезке 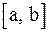 , причем все ее значения
, причем все ее значения 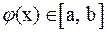 . Тогда, если выполняется условие
. Тогда, если выполняется условие 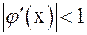 при
при 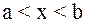 :
:
1) процесс итерации 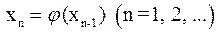 сходится независимо от начального значения
сходится независимо от начального значения 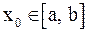 ;
;
2) предельное значение 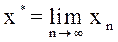 является единственным корнем уравнения
является единственным корнем уравнения 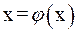 на отрезке
на отрезке 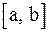 .
.
Доказательство. Так как 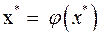 и
и 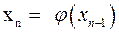 , то можно записать
, то можно записать
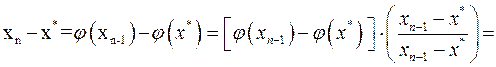
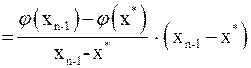 .
.
По теореме о среднем (она утверждает, что если производная функции 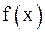 непрерывна на некотором интервале
непрерывна на некотором интервале 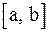 , то тангенс угла наклона хорды, проведенной между точками
, то тангенс угла наклона хорды, проведенной между точками 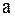 и
и 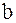 , (т.е.
, (т.е. 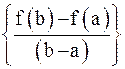 равен производной функции в некоторой промежуточной точке, лежащей между
равен производной функции в некоторой промежуточной точке, лежащей между 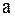 и
и 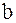 ) частное в последнем выражении будет равно
) частное в последнем выражении будет равно 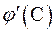 , где
, где 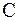 – некоторая промежуточная точка в интервале поиска корня. Следовательно,
– некоторая промежуточная точка в интервале поиска корня. Следовательно, 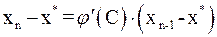 .
.
Если ввести обозначение 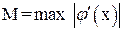 для всего интервала поиска, то предыдущее равенство может быть переписано в виде:
для всего интервала поиска, то предыдущее равенство может быть переписано в виде: 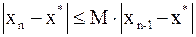
Аналогично 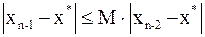 . Тогда для
. Тогда для 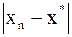 будет справедливо неравенство:
будет справедливо неравенство: 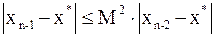 и т. д. Продолжая эти выкладки дальше, в результате получаем
и т. д. Продолжая эти выкладки дальше, в результате получаем 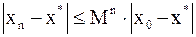 , где
, где 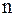 – натуральное число. Таким образом, чтобы метод сходился, необходимо выполнение неравенства:
– натуральное число. Таким образом, чтобы метод сходился, необходимо выполнение неравенства: 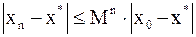 .
.
Отсюда следует, что 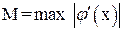 должно быть меньше единицы. В свою очередь, для всех остальных значений
должно быть меньше единицы. В свою очередь, для всех остальных значений 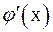 меньших
меньших 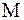 , можно записать:
, можно записать: 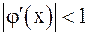 . Число
. Число 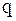 определим из соотношения
определим из соотношения 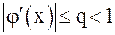 . Тогда справедливо неравенство (вывод см. ниже):
. Тогда справедливо неравенство (вывод см. ниже): 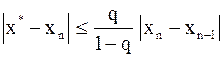 . Если поставить условие, что истинное значение корня
. Если поставить условие, что истинное значение корня 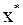 должно отличаться от приближенного значения на величину
должно отличаться от приближенного значения на величину 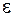 , т.е.
, т.е. 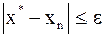 , то приближения
, то приближения 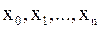 надо вычислять до тех пор, пока не будет выполнено неравенство
надо вычислять до тех пор, пока не будет выполнено неравенство
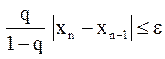 или
или 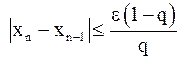 и тогда
и тогда 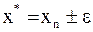 .
.
Вывод неравенства.Рассмотрим два последовательных приближения: 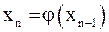 и
и 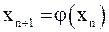 . Отсюда
. Отсюда 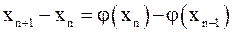 .
.
Используя теорему о среднем, получим:
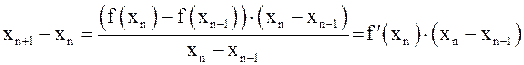 ,
,
тогда на основании условия 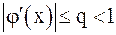 можно записать:
можно записать:
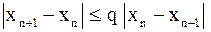 .
.
С другой стороны, пусть 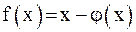 . Очевидно, что
. Очевидно, что 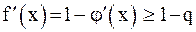 . Отсюда, учитывая, что
. Отсюда, учитывая, что 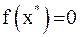 , получим
, получим
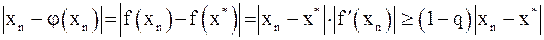 ,
,
где 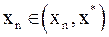 .
.
Тогда 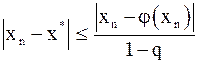 или
или 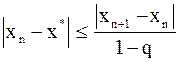 .
.
Используя предыдущую формулу, можно получить:
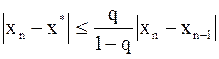 . (5)
. (5)
Перейдём к пределу в равенстве (3), в силу непрерывности функции 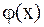 получим
получим 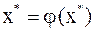 , то есть
, то есть 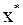 – корень уравнения (2). Других корней на
– корень уравнения (2). Других корней на 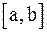 нет, так как если
нет, так как если 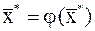 , то
, то 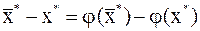 , тогда
, тогда 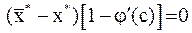 , где
, где 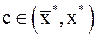 . Равенство нулю будет достигнуто, если
. Равенство нулю будет достигнуто, если 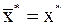 . То есть
. То есть 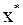 – корень единственный.
– корень единственный.
Теорема доказана.
Приведение уравнения 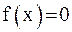 к виду
к виду 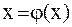
для обеспечения выполнения неравенства 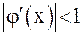
В общем случае получить подходящую итерационную форму возможно, проведя равносильное преобразование исходного уравнения, например, умножив его на коэффициент 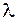 :
: 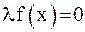 . Прибавив затем к обеим частям уравнения
. Прибавив затем к обеим частям уравнения 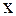 и обозначив
и обозначив 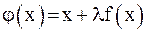 можно потребовать выполнения достаточного условия
можно потребовать выполнения достаточного условия 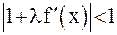 . Отсюда определяется необходимое значение
. Отсюда определяется необходимое значение 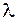
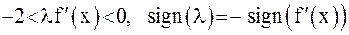 . Так как условие
. Так как условие 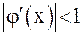 должно выполняться на всем отрезке
должно выполняться на всем отрезке 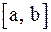 , то для выбора
, то для выбора 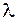 следует использовать наибольшее значение
следует использовать наибольшее значение 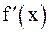 на этом отрезке, т.е.
на этом отрезке, т.е.
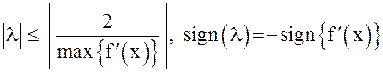 . Это соотношение определяет диапазон значений коэффициента
. Это соотношение определяет диапазон значений коэффициента 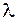 , изменяющий величину
, изменяющий величину 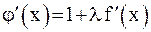 в пределах
в пределах 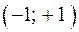 .
.
Обычно принимают 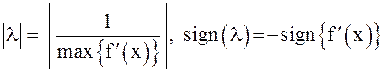 .
.
На рис. 3–6 показаны четыре случая взаимного расположения линий 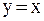 и
и 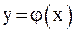 и соответствующие итерационные процессы. Рис. 3 и 4 соответствуют случаю
и соответствующие итерационные процессы. Рис. 3 и 4 соответствуют случаю 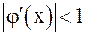 , и итерационный процесс сходится. При этом, если
, и итерационный процесс сходится. При этом, если 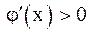 (рис. 3), сходимость носит односторонний характер, а если
(рис. 3), сходимость носит односторонний характер, а если 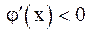 (рис. 4), сходимость носит двусторонний, колебательный характер. Рис. 5 и 6 соответствуют случаю
(рис. 4), сходимость носит двусторонний, колебательный характер. Рис. 5 и 6 соответствуют случаю 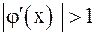 – итерационный процесс расходится. При этом может быть односторонняя (рис. 5) и двусторонняя (рис. 6) расходимость.
– итерационный процесс расходится. При этом может быть односторонняя (рис. 5) и двусторонняя (рис. 6) расходимость.
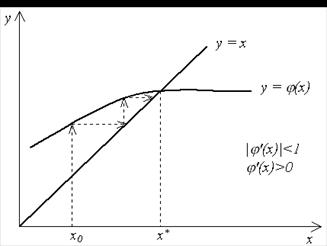
Рис. 3
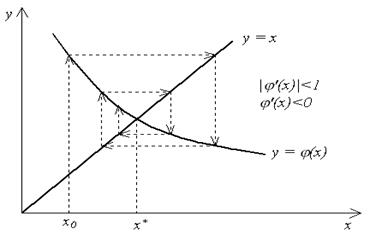
Рис. 4

Рис. 5
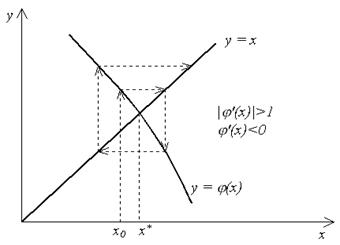
Рис. 6
Погрешность метода. Оценка погрешности была доказана (5).
Критерий окончания. Из оценки (5) следует, что вычисления надо продолжать до выполнения неравенство 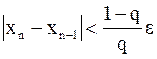 . Если же
. Если же 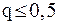 , то оценка упрощается:
, то оценка упрощается: 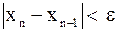 .
.
2.5 Метод Ньютона (метод касательных)
Метод Ньютона является наиболее эффективным методом решения нелинейных уравнений. Пусть корень 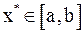 , т. е.
, т. е. 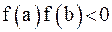 . Предполагаем, что функция
. Предполагаем, что функция 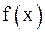 непрерывна на отрезке
непрерывна на отрезке 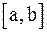 и дважды непрерывно дифференцируема на интервале
и дважды непрерывно дифференцируема на интервале 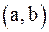 . Положим
. Положим 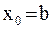 . Проведем касательную к графику функции
. Проведем касательную к графику функции 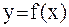 в точке
в точке 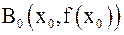 (рис. 8).
(рис. 8).
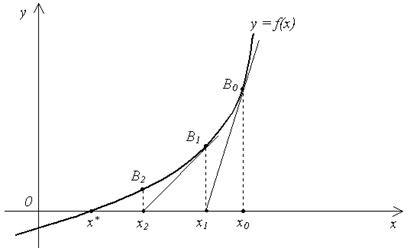
Рис. 8
Уравнение касательной будет иметь вид: 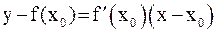 .
.
Первое пересечение получим, взяв абсциссу точки пересечения этой касательной с осью 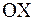 , т. е. положив
, т. е. положив 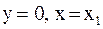 :
: 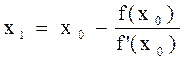 .
.
Аналогично поступим с точкой 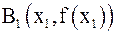 , затем с точкой
, затем с точкой 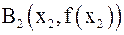 и т. д., в результате получим последовательность приближений
и т. д., в результате получим последовательность приближений 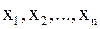 , причем
, причем
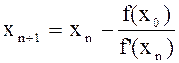 . (6)
. (6)
Формула (6) является расчетной формулой метода Ньютона.
Метод Ньютона можно рассматривать как частный случай метода простых итераций, для которого 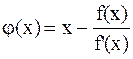 .
.
Сходимость метода. Сходимость метода Ньютона устанавливает следующая теорема.
Теорема. Пусть 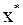 – простой корень уравнения
– простой корень уравнения 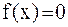 и в некоторой окрестности этого корня функция
и в некоторой окрестности этого корня функция 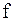 дважды непрерывно дифференцируема. Тогда найдется такая малая
дважды непрерывно дифференцируема. Тогда найдется такая малая 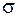 – окрестность корня
– окрестность корня 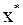 , что при произвольном выборе начального приближения
, что при произвольном выборе начального приближения 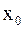 из этой окрестности итерационная последовательность, определенная по формуле (6) не выходит за пределы этой окрестности и справедлива оценка:
из этой окрестности итерационная последовательность, определенная по формуле (6) не выходит за пределы этой окрестности и справедлива оценка:
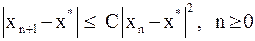 , (7)
, (7)
где 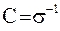 .
.
Сходимость метода Ньютона зависит от того, насколько близко к корню выбрано начальное приближение.
Выбор начального приближения. Пусть 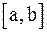 – отрезок, содержащий корень. Если в качестве начального приближения
– отрезок, содержащий корень. Если в качестве начального приближения 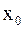 выбрать тот из концов отрезка, для которого
выбрать тот из концов отрезка, для которого 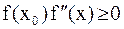 , то итерации (6) сходятся, причем монотонно. Рис. 8 соответствует случаю, когда в качестве начального приближения был выбран правый конец отрезка:
, то итерации (6) сходятся, причем монотонно. Рис. 8 соответствует случаю, когда в качестве начального приближения был выбран правый конец отрезка: 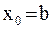 (Здесь
(Здесь  ).
).
Погрешность метода. Оценка (7) неудобна для практического использования. На практике пользуются следующие оценки погрешности:
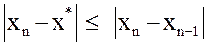 . (8)
. (8)
Критерий окончания. Оценка (8) позволяет сформулировать следующий критерий окончания итераций метода Ньютона. При заданной точности 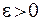 вычисления нужно вести до тех пор, пока не будет выполнено неравенство
вычисления нужно вести до тех пор, пока не будет выполнено неравенство
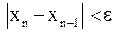 .
.
2.6 Видоизменённый метод Ньютона
Если производная 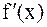 мало изменяется на отрезке
мало изменяется на отрезке 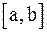 , то в расчетной формуле метода можно положить:
, то в расчетной формуле метода можно положить: 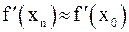 . Отсюда для корня
. Отсюда для корня 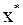 уравнения
уравнения 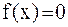 получаем последовательные приближения
получаем последовательные приближения
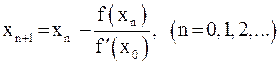 .
.
Геометрически этот способ означает, что касательные заменяются прямыми, параллельными касательной к кривой 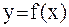 , в ее фиксированной точке
, в ее фиксированной точке 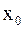 . Этот способ избавляет от необходимости вычислять каждый раз значения производной, поэтому эта формула полезна, если
. Этот способ избавляет от необходимости вычислять каждый раз значения производной, поэтому эта формула полезна, если 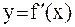 сложна.
сложна.
2.7 Метод хорд
Рассмотрим еще одну модификацию метода Ньютона. Пусть известно, что простой корень 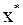 уравнения
уравнения 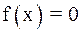 находится на отрезке
находится на отрезке 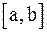 , то есть
, то есть 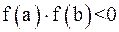 . И предположим, что
. И предположим, что 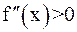 при
при 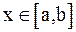 (если это не так, то будем рассматривать уравнение
(если это не так, то будем рассматривать уравнение 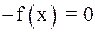 ). Заменим кривую
). Заменим кривую 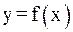 хордой
хордой 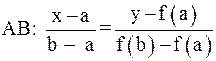 .
.
| 
|
| а)
| б)
|
| Рис. 10
|
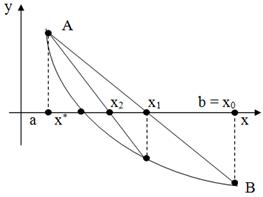
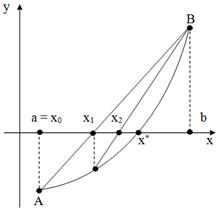
Возможны два случая: 1) 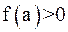 (рис. 9); 2)
(рис. 9); 2) 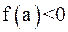 (рис. 10). В первом случае конец
(рис. 10). В первом случае конец 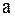 неподвижен и последовательные приближения:
неподвижен и последовательные приближения: 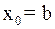
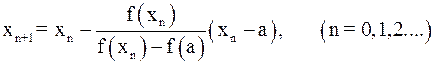 (9)
(9)
образуют ограниченную монотонно убывающую последовательность, причем 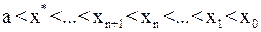 .
.
Во втором случае неподвижен конец 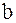 , а последовательные приближения:
, а последовательные приближения: 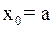
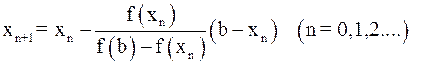 (10)
(10)
образуют ограниченную монотонно убывающую последовательность, причем 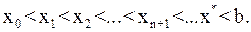 Итак, в результате получаем следующее
Итак, в результате получаем следующее
Выбор начального условия:
1. Рассматриваем только случай 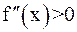 (иначе
(иначе 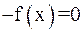 ).
).
2. Начальное приближение x0 выбираем из условия 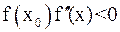
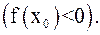
Неподвижен тот конец, для которого знак функции совпадает со знаком ее второй производной.
Критерий окончания. Критерий окончания итераций метода хорд такой же, как и для метода Ньютона. При заданной точности 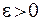 вычисления нужно вести до тех пор, пока не будет выполнено неравенство
вычисления нужно вести до тех пор, пока не будет выполнено неравенство 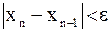 .
.
1.8. Комбинированный метод
Пусть 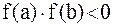 , а
, а 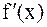 и
и 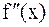 сохраняют постоянные знаки на отрезке
сохраняют постоянные знаки на отрезке 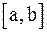 . Соединяя методы хорд и касательных, получаем метод на каждом этапе, которого находим значения по недостатку и значения по избытку точного корня
. Соединяя методы хорд и касательных, получаем метод на каждом этапе, которого находим значения по недостатку и значения по избытку точного корня 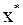 уравнения
уравнения 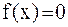 . Пусть
. Пусть 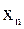 – последовательные приближения метода хорд,
– последовательные приближения метода хорд, 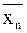 – последовательные приближения метода касательных. Пошаговая иллюстрация представлена на рис. 11.
– последовательные приближения метода касательных. Пошаговая иллюстрация представлена на рис. 11.
Возможны 4 случая: 1) 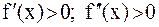 , 2)
, 2) 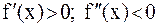 ,
,
3) 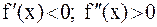 , 4)
, 4) 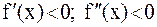 ,
,
которые можно свести к первому случаю.
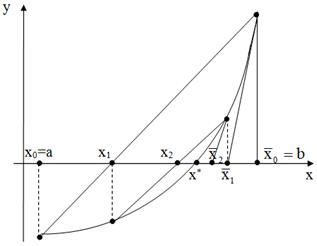
Рис. 11
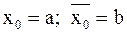 .
.
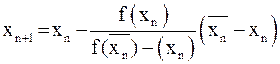 .
. 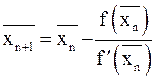 .
.
Очевидно, что 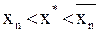 и
и 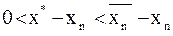 .
.
По окончании процесса за значение корня 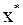 лучше всего взять среднее арифметическое полученных значений:
лучше всего взять среднее арифметическое полученных значений: 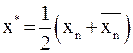 .
.
3. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ
АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
3.1 Постановка задачи
Требуется найти решение системы линейных уравнений:
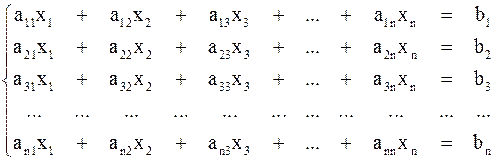
или в матричной форме: 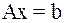 , где
, где
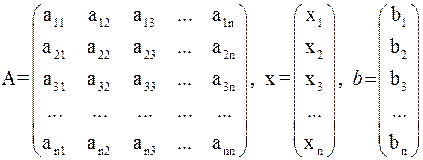
По правилу Крамера система 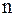 линейных уравнений имеет единственное решение, если определитель системы отличен от нуля
линейных уравнений имеет единственное решение, если определитель системы отличен от нуля 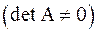 и значение каждого из неизвестных определяется следующим образом:
и значение каждого из неизвестных определяется следующим образом: 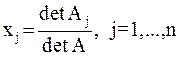 , где
, где  – определитель матрицы, получаемой заме-
– определитель матрицы, получаемой заме-
ной 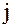 -го столбца матрицы
-го столбца матрицы 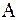 столбцом правых частей
столбцом правых частей 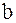 .
.
Непосредственный расчет определителей для больших 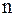 является очень трудоемким.
является очень трудоемким.
Известные в настоящее время многочисленные приближенные методы решения систем линейных алгебраических уравнений распадаются на две большие группы: прямые методы и методы итераций.
Прямые методы всегда гарантируют получение решения, если оно существуют, однако, для больших 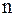 требуется большое количество операций, и возникает опасность накопления погрешностей.
требуется большое количество операций, и возникает опасность накопления погрешностей.
Этого недостатка лишены итерационные методы, но зато они не всегда сходятся и могут применяться лишь для систем определенных классов.
Норма матрицы является некоторой обобщенной оценкой значений элементов матрицы. Для её вычисления можно использовать следующие выражения:
 ,
,
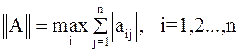 ,
, 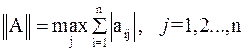 .
.
3.2 Метод простой итерации
Для того чтобы применить метод простой итерации, необходимо систему уравнений
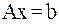 (1)
(1)
с квадратной невырожденной матрицей 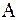 привести к виду
привести к виду
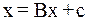 , (2)
, (2)
где 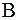 – квадратная невырожденная матрица с элементами
– квадратная невырожденная матрица с элементами 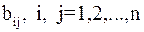 ,
,
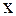 – вектор-столбец неизвестных
– вектор-столбец неизвестных 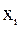 ,
, 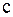 – вектор-столбец с элементами
– вектор-столбец с элементами 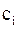 ,
, 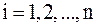 . Существуют различные способы приведения системы (1) к виду (2). Рассмотрим самый простой.
. Существуют различные способы приведения системы (1) к виду (2). Рассмотрим самый простой.
Представим систему в развернутом виде:
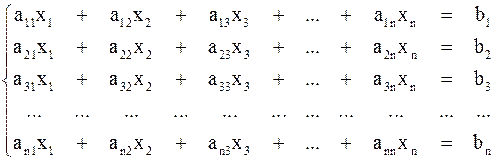 (3)
(3)
Из первого уравнения системы (3) выразим неизвестную 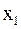 :
:
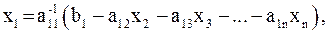 из второго уравнения – неизвестную
из второго уравнения – неизвестную 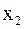 :
:
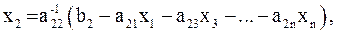 и т. д. В результате получим систему:
и т. д. В результате получим систему:
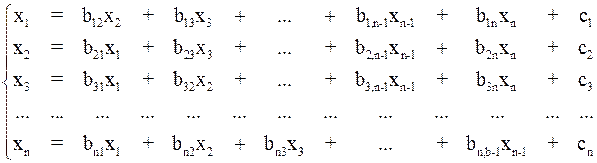 (4)
(4)
Матричная запись системы (4) имеет вид (2). На главной диагонали матрицы  находятся нулевые элементы, а остальные элементы вычисляются по формулам:
находятся нулевые элементы, а остальные элементы вычисляются по формулам:
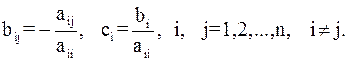 (5)
(5)
Очевидно, что диагональные элементы матрицы  должны быть отличны от нуля. Выберем произвольно начальное приближение. Обычно в качестве первого приближения берут
должны быть отличны от нуля. Выберем произвольно начальное приближение. Обычно в качестве первого приближения берут 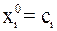 или
или 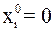 . Подставим начальное приближение в правую часть (4). Вычисляя левые части, получим значения
. Подставим начальное приближение в правую часть (4). Вычисляя левые части, получим значения 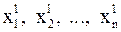 . Продолжая этот процесс дальше, получим последовательность приближений, причем
. Продолжая этот процесс дальше, получим последовательность приближений, причем 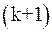 приближение строится следующим образом:
приближение строится следующим образом:
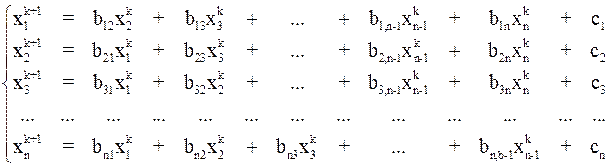
Последняя система представляет собой расчетные формулы метода простой итерации.
Сходимость метода простой итерации. Известно следующее достаточное условие сходимости метода простой итерации.
Если элементы матрицы 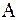 удовлетворяют условию:
удовлетворяют условию:
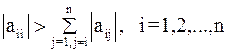 , (6)
, (6)
то итерационная последовательность 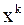 сходится к точному решению
сходится к точному решению 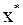 .
.
Условие (7) называют условием преобладания диагональных элементов матрицы 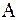 , так как оно означает, что модуль диагонального элемента
, так как оно означает, что модуль диагонального элемента 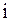 -ой строки больше суммы модулей остальных элементов этой строки,
-ой строки больше суммы модулей остальных элементов этой строки, 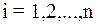 .
.
Необходимо помнить, что условие сходимости (6) является лишь достаточным. Его выполнение гарантирует сходимость метода простых итераций, но его невыполнение, вообще говоря, не означает, что метод расходится.
Справедлива следующая оценка погрешности:
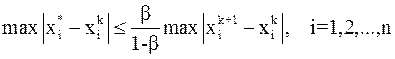 , (7)
, (7)
где 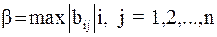 .
.
Правую часть оценки (7) легко вычислить после нахождения очередного приближения.
Иначе достаточное условие (6) для матрицы 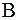 может быть переформулирована так: если
может быть переформулирована так: если 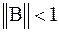 , то итерационный процесс (6) сходится к точному решению системы.
, то итерационный процесс (6) сходится к точному решению системы.
Критерий окончания. Если требуется найти решение с точностью 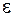 , то в силу (7) итерационный процесс следует закончить, как только на
, то в силу (7) итерационный процесс следует закончить, как только на 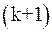 -ом шаге выполнится неравенство:
-ом шаге выполнится неравенство: 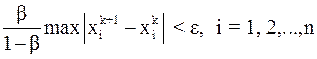 .
.
Поэтому в качестве критерия окончания итерационного процесса можно использовать неравенство 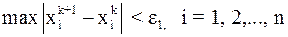 , где
, где 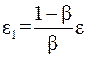 .
.
Если выполняется условие 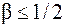 , то можно пользоваться более простым критерием окончания:
, то можно пользоваться более простым критерием окончания:
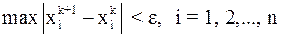 . (8)
. (8)
В других случаях использование последнего критерия (8) неправомерно и может привести к преждевременному окончанию итерационного процесса.
Метод Зейделя
Модификацией метода простой итерации можно считать метод Зейделя.
В методе простой итерации на 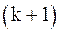 -ой итерации значения
-ой итерации значения 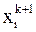 ,
, 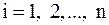 вычисляются подстановкой в правую часть (6) вычисленных на предыдущей итерации значений. В методе Зейделя при вычислении
вычисляются подстановкой в правую часть (6) вычисленных на предыдущей итерации значений. В методе Зейделя при вычислении 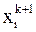 используются значения
используются значения 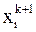 ,
, 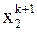 ,
, 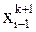 , уже найденные на
, уже найденные на 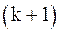 -ой итерации, а не
-ой итерации, а не 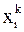 ,
, 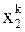 , …,
, …, 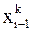 , как в методе простой итерации, т.е.
, как в методе простой итерации, т.е. 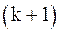 -е приближение строится следующим образом:
-е приближение строится следующим образом:
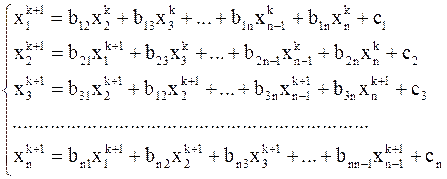 (9)
(9)
Эти формулы являются расчетными формулами метода Зейделя.
Введем нижнюю и верхнюю треугольные матрицы:
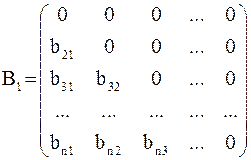 и
и 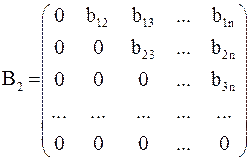 .
.
Матричная запись расчетных формул (9) имеет вид: 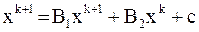 . Так как
. Так как 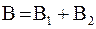 , точное решение
, точное решение 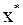 исходной системы удовлетворяет равенству:
исходной системы удовлетворяет равенству:  .
.
Сходимость метода Зейделя. Достаточным условием сходимости метода Зейделя является выполнение неравенства:
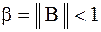 . (10)
. (10)
Неравенство (10) означает, что для сходимости метода Зейделя достаточно, чтобы любая норма матрицы 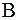 был меньше единицы.
был меньше единицы.
Если выполнено условие (10), то справедлива следующая оценка погрешности:
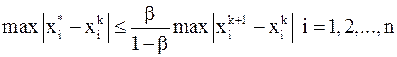 , (11)
, (11)
где 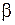 – норма матрицы
– норма матрицы 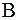 .
.
Критерий окончания. Если требуется найти решение с точностью 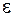 , итерационный процесс следует закончить, как только на
, итерационный процесс следует закончить, как только на 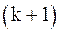 -ом шаге выполнится неравенство:
-ом шаге выполнится неравенство: 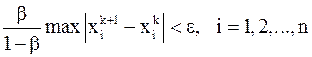 . Поэтому в качестве критерия окончания итерационного процесса можно использовать неравенство
. Поэтому в качестве критерия окончания итерационного процесса можно использовать неравенство 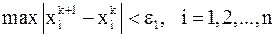 , где
, где 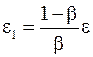 . Если выполняется условие
. Если выполняется условие
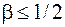 , то можно пользоваться более простым критерием окончания:
, то можно пользоваться более простым критерием окончания:
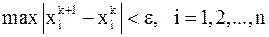 .
.
Метод Зейделя, как правило, сходится быстрее, чем метод простой итерации. Однако возможны ситуации, когда метод простой итерации сходится, а метод Зейделя сходится медленнее или вообще расходится.
Сравнение с предыдущим примером показывает, что метод Зейделя сходится быстрее и дает более точный результат.
Популярное:

