Скалярное, векторное, смешанное произведение векторов.

Пример 1. Найти угол между векторами и , если , , , .

Решение. Используем формулу . Определим координаты векторов и , учитывая, что при сложении векторов мы складываем одноименные координаты, а при умножении вектора на число – умножаем на это число каждую координату этого вектора, а: , .

Найдем скалярное произведение векторов и и их длины. , , . Подставив в формулу, получим . Отсюда .

Пример 2. Параллелограмм построен на векторах и , где , , 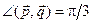. Вычислить длину диагоналей этого параллелограмма, угол между диагоналями и площадь параллелограмма.

 

Решение.

, ,

.

Угол между диагоналями обозначим буквой , тогда

Следовательно, .

Используя свойства векторного произведения, вычислим площадь параллелограмма:

Пример 3. Компланарны ли векторы , , ?

Решение. Если векторы компланарны, то по свойству 4) их смешанное произведение равно нулю. Проверим это. Найдем смешанное произведение данных векторов, вычислив определитель:

векторы , , некомпланарны.

Пример 4. Найти точку , делящую отрезок в отношении , если .

Решение. Определим координаты точки :

. Таким образом, .

Пример 5. Пирамида задана координатами своих вершин , , . Требуется найти: 1) длины ребер и ; 2) угол между ребрами и ; 3) площадь грани, содержащей вершины ; 4) объем пирамиды; 5) уравнения прямых и ; 6) уравнение высоты , опущенной из вершины на плоскость ; 7) расстояние от вершины до плоскости ; 8) угол между ребром и гранью, содержащей вершины .

Решение. 1) Длины ребер и определим как модуль векторов и по формулам ;

;

2) Найдем координаты векторов и :

Длины этих векторов, т.е. длины ребер и , таковы: ,

. Косинус угла между ребрами и вычислим по формуле

;

3) Площадь грани (треугольника) равна половине площади параллелограмма, построенного на векторах и , т.е. половина модуля векторного произведения этих векторов, которое равно

.

Тогда, (кв. ед);

4) Объем пирамиды равен .

(куб. ед);

5) Уравнения прямых и найдем как уравнения прямых, проходящих через две данные точки:

( ): ,

( ): (абсциссы точек и одинаковые);

6) Направляющим вектором высоты является нормальный вектор плоскости . Получим уравнение плоскости :

,

– уравнение плоскости . Тогда нормальный вектор плоскости имеет координаты . Канонические уравнения прямой, проходящей через точку параллельно вектору имеет вид: ;

7) Для вычисления расстояния от вершины до плоскости воспользуемся формулой . В нашем случае – уравнение плоскости и . Итак, ;

8) Угол между прямой и плоскостью находят по формуле:

, где – нормальный вектор плоскости . и (см. п.7) .

Таким образом, ,

.

Задания для самостоятельной работы

1. Найти угол между векторами и , если , .

А) , ,

Б) , ,

В) , ,

2. Параллелограмм построен на векторах и , где А) , , .

Б) , , .

В) , , .

Вычислить длину диагоналей этого параллелограмма, угол между диагоналями и площадь параллелограмма.

2. Компланарны ли векторы

А) , , ,

Б) , , ,

В) , , ?

3. Найти точку , делящую отрезок в отношении , если

А) .

Б) .

В) .

4. Пирамида задана координатами своих вершин

А) , , ,

Б) , , ,

В) , , .

Требуется найти: 1) длины ребер и ; 2) угол между ребрами и ; 3) площадь грани, содержащей вершины ; 4) объем пирамиды; 5) уравнения прямых и ; 6) уравнение высоты , опущенной из вершины на плоскость ; 7) расстояние от вершины до плоскости ; 8) угол между ребром и гранью, содержащей вершины .

Форма контроля: Проверка решений задач и заданий

4. Функции комплексного пременного

 

 

Форма контроля: Проверка решений задач и заданий

Дифференциальное и интегральное исчисления

Пределы.

Пример: Найти пределы функций

а) б)

в) г)

д) е)

ж) з)

 

Решение:

а) Непосредственная подстановка предельного значения аргумента x=2 приводит к неопределённости вида (0/0). Чтобы раскрыть эту неопределённость, разложим числитель и знаменатель на множители по формуле где x₁ и x₂ находятся как корни квадратных трёхчленов стоящих в числители и знаменатели

Так как аргумент x только стремится к своему предельному значению -2, но не совпадает с ним, то множитель (x+2) отличен от нуля при х → -2 и можно сократить на (x+2). В результате будем иметь:

б) При x® ¥ имеем неопределенность вида (¥ / ¥ ). Разделим числитель и знаменатель дроби на x² (x¹ 0) при х ®¥. Получим:

= = 2,

(так как при х ®¥ 7/x ® 0, 6/x²® 0, 5/x ® 0, 9/x²® 0).

в) Непосредственная подстановка даёт неопределённость вида(0/0).

Используем формулу сокращённого умножения (a-b)(a+b)=a² +b². Умножим числитель и знаменатель дроби на выражения: и .

Имеем:

г) При х ®¥ основание стремится к 1, а показатель степени (4x+1) стремится к ¥. Значит, имеем неопределённость вида (1^¥ ).

Будем использовать второй замечательный предел .

Сведем исходное выражение заданного предела ко второму замечательному пределу:

 

Положим . Тогда . Выразим показатель степени через переменную :

Кроме того, при х ®¥, новая переменная y ®¥.

Таким образом

 

Задания для самостоятельной работы

 

1) а) б) в) г)

2) а) б) в) г)

3) а) б) в) г)

4) а) б) в) г)

5) а) б) в) г)

6) а) б) в) г)

7) а) б) в) г)

8) а) б) в) г)

9) а) б) в) г)

10) а) б) в) г)

 

Форма контроля: Проверка решений задач и заданий

⇐ Предыдущая12345678910Следующая ⇒

Поделиться: