Метод контурных токов (КТ)

Можно показать, что из p – токов ветвей только токи главных ветвей числом p – q + 1 являются независимыми, обычно q – 1<p.

 Будем называть их контурными токами. Остальные токи, т.е. ветвей дерева, могут быть найдены из контурных, применяя УБТ.

 Для примера №1 УБТ:

Токи главных ветвей:

Тогда токи ветвей дерева:

Подставим в УБН, получим систему контурных уравнений цепи:

Введем новые понятия:

Собственным сопротивлением  i-гo контура назовем сумму сопротивлений всех ветвей, входящих в этот контур.

Контурный ток i-гo контура обозначим , направление совпадает с направлением главной ветви контура:

Общим или взаимным сопротивлением i-гo и j-гo контуров назовем сопротивление , равное сумме сопротивлений ветвей, общих для этих контуров.

 Общее сопротивление  берется со знаком плюс, если направление соответствующих контурных токов в этих ветвях совпадает.

 Если контуры не имеют общих ветвей, то общее сопротивление равно нулю.

Контурная ЭДС i-го контура — алгебраическая сумма ЭДС всех идеализированных источников напряжения, входящих в данный контур.

 Если направление ЭДС совпадает с направлением контурного тока, плюс.

Контурные уравнения в канонической (стандартной) форме:

 Такая же система уравнений будет для цепи, содержащей произвольное n число главных контуров.

 В матричной форме система контурных уравнений: i=1,…,n; j=1,…,n;

 где n = р − q + 1

— квадратная симметричная  матрица контурных сопротивлений;

Система уравнений решается любым из известных способов: Крамера, Гаусса L? – преобразований и др.

 При наличии ветвей с источниками тока                                                                 их либо преобразуют в ветви с источниками напряжения, либо при выборе дерева графа все источники тока заданы и не требуют определения.

 Для неизвестных контурных токов составляется система из р − q + 1 –р_ит уравнений.

 Таким образом, порядок составления контурных уравнений следующий:

 1) построение графа цепи, выбор дерева графа, выделение главных контуров;

2) определение числа уравнений n и запись системы в канонической;

3) нахождение элементов матриц контурных сопротивлений  и контурных ЭДС .

Метод узловых напряжений

Узловое напряжение – это напряжение i– го узла цепи относительно базового .

Напряжения всех ветвей цепи могут быть выражены через узловые:

−

 

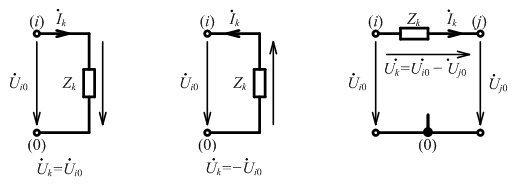
Если цепь не содержит вырожденных ветвей р_ин, то все q – 1 неизвестные узловые напряжения независимы.

 ССУ относительно узловых напряжений называется системой узловых уравнений цепи.

 Метод формирования такой системы называется методом узловых напряжений.

 Преобразуем схему замещения примера 1 к виду:

 

 

 

УБТ:

Выразим токи ветвей через напряжение ветвей, а напряжение ветвей через узловые напряжения:

Представим в УБТ:

Введем понятия:

Собственная проводимость  i-го узла назовем сумму проводимостей всех ветвей, подключенных к данному узлу:

Общая (взаимная) проводимость i-гo и j-гo узлов  — это сумма проводимостей всех ветвей, включенных непосредственно между этими узлами, взятая с противоположным знаком.

 Если в цепи нет ветви между i-м и j-м узлами, то  = 0.

Узловым током   i-гo узла называется алгебраическая сумма токов всех источников тока, подключенных к данному узлу.

 Если источник тока направлен к узлу, то плюс.

Таким образом, узловые уравнения в канонической форме:

Для цепи с m=q – 1 независимыми узлами в матричной форме:

i=1,…,m; j=1,…,m;

 

При  при составлении узловых уравнений нет необходимости строить граф.

При наличии источников напряжения в цепи они либо с помощью эквивалентных преобразований преобразуются в источники тока, либо включаются в дерево графа, затем определяется  независимых узлов и узловых напряжений, для  главных сечений, соответствующих невырожденным ветвям дерева, составляются уравнения БТ и далее по алгоритму.

⇐ Предыдущая45678910111213Следующая ⇒

Поделиться: