Оптимизация коррекции траектории космического аппарата
Рассмотрим возможность применения комбинированного метода к задаче оптимизации процесса однопараметрической коррекции траектории космического аппарата.
По-прежнему через 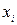 обозначим величину прогнозируемого конечного промаха в момент, непосредственно предшествующий i-му корректирующему импульсу, отнесенному к среднему квадратичному отклонению априорного промаха; через
обозначим величину прогнозируемого конечного промаха в момент, непосредственно предшествующий i-му корректирующему импульсу, отнесенному к среднему квадратичному отклонению априорного промаха; через  — расчетную величину i-го корректирующего импульса скорости, отнесенную к среднему квадратичному отклонению ошибки, его реализации, через
— расчетную величину i-го корректирующего импульса скорости, отнесенную к среднему квадратичному отклонению ошибки, его реализации, через  — производную по направлению
— производную по направлению 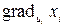 . Обычно
. Обычно 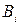 убывает по мере движения аппарата. Тогда после отработки i-го импульса получим
убывает по мере движения аппарата. Тогда после отработки i-го импульса получим

| (18.49)
|
где  представляет собой ошибку реализации i-го корректирующего импульса. Будем считать, что
представляет собой ошибку реализации i-го корректирующего импульса. Будем считать, что  =0 при
=0 при  =0.При
=0.При 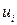 ¹ 0
¹ 0  — центрированная случайная гауссовская величина с единичной дисперсией. Задача оптимизации процесса коррекции состоит в определении последовательности
— центрированная случайная гауссовская величина с единичной дисперсией. Задача оптимизации процесса коррекции состоит в определении последовательности  , i= 1, ..., N, включая определение самих моментов коррекции, обеспечивающей достижение требуемой конечной точности, характеризуемой условием
, i= 1, ..., N, включая определение самих моментов коррекции, обеспечивающей достижение требуемой конечной точности, характеризуемой условием
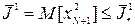
| (18.50)
|
при минимальном расходе топлива, оцениваемом величиной

| (18.51)
|
Число коррекций N и величина 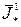 в соотношении (18.23) считаются заданными. Так как от моментов коррекции зависят лишь коэффициенты
в соотношении (18.23) считаются заданными. Так как от моментов коррекции зависят лишь коэффициенты  , то задачу определения оптимальных моментов коррекции, т. е. задачу оптимального распределения корректирующих импульсов вдоль траектории наведения, будем трактовать как задачу отыскания оптимальной последовательности
, то задачу определения оптимальных моментов коррекции, т. е. задачу оптимального распределения корректирующих импульсов вдоль траектории наведения, будем трактовать как задачу отыскания оптимальной последовательности 
Для решения задачи обратимся к комбинированному методу оптимизации.
Согласно поэтапной оптимизации решение задачи может быть проведено в два этапа. На первом этапе при фиксированной последовательности В путем минимизации критерия (18.51) по последовательности  i=l, 2,..., N, с учетом (18.50) отыскивается алгоритм оптимальной коррекции и функция
i=l, 2,..., N, с учетом (18.50) отыскивается алгоритм оптимальной коррекции и функция
представляющая собой по сути дела зависимость потребного для достижения заданной конечной точности расхода топлива от моментов проведения коррекции.
На втором этапе находится оптимальное распределение корректирующих импульсов путем минимизации функции  по последовательности
по последовательности 
Для решения задачи первого этапа воспользуемся методом множителей Лагранжа.
Введем в рассмотрение обобщенный критерий оптимальности
Пусть  управление, минимизирующее
управление, минимизирующее 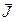 при данном a.
при данном a.
Нетрудно показать, что если найдется такой множитель a> 0, что будут одновременно выполнены условия
то управление  будет оптимальным в задаче первого этапа. Действительно, из определения
будет оптимальным в задаче первого этапа. Действительно, из определения  следует
следует
откуда 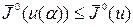 для всех и, если
для всех и, если  . Таким образом, для определения алгоритма оптимальной коррекции достаточно минимизировать по последовательности
. Таким образом, для определения алгоритма оптимальной коррекции достаточно минимизировать по последовательности  обобщенный критерий оптимальности
обобщенный критерий оптимальности 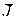 последующим выбором множителя a из условия
последующим выбором множителя a из условия  .
.
Минимизация критерия 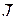 может быть проведена с помощью основного рекуррентного соотношения метода динамического программирования
может быть проведена с помощью основного рекуррентного соотношения метода динамического программирования

| (18.52)
|
при граничном условии
Для определения множителя a необходимо произвести анализ конечной точности при найденном алгоритме коррекции, т. е. установить зависимость  от a. С этой целью может быть использовано рекуррентное соотношение
от a. С этой целью может быть использовано рекуррентное соотношение
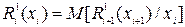
| (18.53)
|
при граничном условии
Искомая зависимость определится соотношением
Для решения задачи второго этапа необходимо установить зависимость  . Это может быть сделано с помощью рекуррентного соотношения
. Это может быть сделано с помощью рекуррентного соотношения

| (18.54)
|
при граничном условии
Так как функция  характеризует зависимость ожидаемого расхода топлива при оптимальном корректировании от текущего состояния
характеризует зависимость ожидаемого расхода топлива при оптимальном корректировании от текущего состояния  , то, очевидно,
, то, очевидно,
Для окончательного решения задачи остается минимизировать функцию 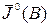 по В.
по В.
Для простоты ограничимся рассмотрением случая одноимпульсной коррекции. Предположим, что единственная коррекция производится в момент i= N. Воспользовавшись рекуррентным соотношением (18.52), с учетом (18.49) получим
где
Осуществляя операцию минимизации по  для случая
для случая  > 0, получаем
> 0, получаем
Минимальное значение функции  при этом оказывается равным
при этом оказывается равным
где
Аналогично для случая  < 0
< 0
Объединяя полученные результаты, заключаем, что оптимальный алгоритм коррекции в момент i= N имеет вид
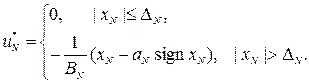
| (18.55)
|
Здесь  — величина, определяемая условием
— величина, определяемая условием

|
|
т.е. 
|
|
Таким образом, алгоритм оптимальной коррекции является существенно нелинейным. Он имеет зону нечувствительности и является линейным вне этой зоны.
Функция потерь 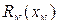 при найденном алгоритме может быть представлена в виде
при найденном алгоритме может быть представлена в виде

| (18.56)
|
В соответствии с изложенной выше методикой для определения множителя a, входящего в алгоритм (18.55) через параметр  , необходимо установить зависимость
, необходимо установить зависимость 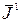 от a. Для этого, как уже говорилось, воспользуемся рекуррентным соотношением (18.53), полагая i= N. Будем иметь
от a. Для этого, как уже говорилось, воспользуемся рекуррентным соотношением (18.53), полагая i= N. Будем иметь
или, принимая во внимание алгоритм (18.55),

| (18.57)
|
где  .
.
Так как рассматривается случай одноимпульсной коррекции, то в соответствии с принятыми обозначениями  представляет собой величину нормированного априорного промаха, который имел бы место без коррекции траектории. Полагая, что
представляет собой величину нормированного априорного промаха, который имел бы место без коррекции траектории. Полагая, что  является центрированной случайной величиной с нормальным законом распределения и единичной дисперсией и производя осреднение выражения (18.48) по
является центрированной случайной величиной с нормальным законом распределения и единичной дисперсией и производя осреднение выражения (18.48) по  , получим искомую зависимость
, получим искомую зависимость 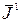 от a.
от a.
Введем условные обозначения для следующих интегралов
Эти интегралы легко выражаются через табличные интегралы вероятностей, а именно,
Здесь
С учетом принятых обозначении получаем
или
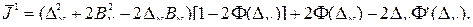
| (18.58)
|
Соотношение (18.58) и устанавливает зависимость  от множителя Лагранжа a, в данном случае через параметр
от множителя Лагранжа a, в данном случае через параметр  , который связан с a следующим соотношением
, который связан с a следующим соотношением
Каждому значению a или, что то же самое,  соответствует свое значение
соответствует свое значение 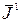 . Приравнивая
. Приравнивая 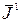 величине
величине  , получаем уравнение для определения a (или
, получаем уравнение для определения a (или  ):
):

| (18.59)
|
К сожалению, аналитически решить уравнение относительно  не удается. Решение можно получить численными методами или графически, построив зависимость
не удается. Решение можно получить численными методами или графически, построив зависимость 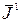 от
от  . Характерно, что эта зависимость является монотонно возрастающей, в чем нетрудно убедиться, рассмотрев производную
. Характерно, что эта зависимость является монотонно возрастающей, в чем нетрудно убедиться, рассмотрев производную
Это означает, что решение уравнения (18.59), если такое существует, единственное. Это решение, естественно, зависит от параметра  , определяемого в свою очередь моментом проведения коррекции. С целью определения оптимального момента коррекции установим связь ожидаемого расхода топлива
, определяемого в свою очередь моментом проведения коррекции. С целью определения оптимального момента коррекции установим связь ожидаемого расхода топлива  от величины
от величины 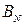 .
.
В соответствии с рекуррентным соотношением (18.54) имеем
где
Производя осреднение полученного выражения по  , как и выше, получаем
, как и выше, получаем
или

| (18.60)
|
Из (18.60) видно, что ожидаемый расход топлива  однозначно определяется все теми же параметрами
однозначно определяется все теми же параметрами  и
и  . Минимизируя (18.60) по
. Минимизируя (18.60) по  с учетом (18.59) найдем оптимальное значение, а следовательно, и оптимальный момент проведения коррекции, обеспечивающие минимум ожидаемому расходу топлива при достижении требуемой конечной точности. Беря производную от (18.60) с учетом (18.59) и приравнивая ее к нулю, получим
с учетом (18.59) найдем оптимальное значение, а следовательно, и оптимальный момент проведения коррекции, обеспечивающие минимум ожидаемому расходу топлива при достижении требуемой конечной точности. Беря производную от (18.60) с учетом (18.59) и приравнивая ее к нулю, получим
причем
Учитывая это, нетрудно получить следующее алгебраическое уравнение второй степени относительно 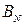
где через 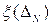 обозначено отношение:
обозначено отношение:
Уравнение имеет единственный положительный корень
Последнее соотношение совместно с условием (18.59) и определяет оптимальное значение коэффициента  , обеспечивающее минимум ожидаемого расхода топлива при достижении требуемой конечной точности. Уравнение (18.59) целесообразно решать графически. С этой целью достаточно построить зависимости
, обеспечивающее минимум ожидаемого расхода топлива при достижении требуемой конечной точности. Уравнение (18.59) целесообразно решать графически. С этой целью достаточно построить зависимости  ,
,  и
и  . На основании зависимости
. На основании зависимости  по заданному значению
по заданному значению 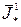 определяется величина
определяется величина  , а по зависимостям
, а по зависимостям  ,
,  и найденной величине
и найденной величине  — оптимальное значение
— оптимальное значение  и соответствующее значение
и соответствующее значение  . Указанные зависимости можно перестроить, исключив вообще из рассмотрения параметр
. Указанные зависимости можно перестроить, исключив вообще из рассмотрения параметр  . В результате получим явные зависимости оптимальных значений
. В результате получим явные зависимости оптимальных значений  и
и  от величины
от величины 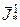 , определяющей заданную конечную точность.
, определяющей заданную конечную точность.

