Выбор материалов и допускаемых напряжений, расчет передач

⇐ ПредыдущаяСтр 14 из 14

Цилиндрическая зубчатая передача, в заданной схеме привода, является тихоходной ступенью двухступенчатого коническо-цилиндрического редуктора.

2.1. Выбор материалов зубчатых колёс и термической обработки тихоходной ступени

2.1.1 Назначаем для колеса и для шестерни сталь 40х улучшенную с твердостью:

-для шестерни

HB₃ =0, 5∙ (HBmax+HBmin) = 0, 5∙ (260+280) = 270 МПа

-для колеса

HB₄ = 0, 5∙ (HBmax+HBmin) = 0, 5∙ (230+260) = 245 МПа

где: HBmin – минимарльная твёрдость колеса в единицах Бринелля

HBmax – максимальная твёрдость колеса в единицах Бринелля

2.1.2 Оцениваем возможность приработки колес:

HB₃ > HB₄ + (10…15);

270 МПа > 255…260 МПа

Условия приработки выполнены

2.1.3Предел контактной выносливости при пульсирующем (отнулевом) цикле напряжений

-для шестерни

-для колеса

2.1.4 Расчетное число циклов при постоянной нагрузке [2]

- для шестерни

-для колеса

где: L_h= 10000 – ресурс работы передачи, ч

n – число оборотов ступени

С = 1- число зацепления зуба за один оборот колеса

2.1.5 Базовое число циклов напряжений

- для шестерни

-для колеса

2.1.6 Коэффициент долговечности

- для шестерни

-для колеса

2.1.7 Допустимые контактные напряжения [2]

- для шестерни

-для колеса

где: S_H = 1, 1 – коэффициент запаса прочности

2.1.8 Расчетное допустимое контактное напряжение

В нашем случае > поэтому принимаем в качестве расчетного допустимого контактного напряжения =488, 2 МПа

Для определения допустимых напряжений изгиба принимаем коэффициент запаса прочности S_F = 1, 7; предел выносливости зубьев на изгиб для данного материала определяется как

2.1.9 Коэффициент долговечности при расчете на изгибную выносливость

- для шестерни

- для колеса

Согласно условию 1≤ Y_N≤ 4 принимаем Y_N₃= Y_N₄=1.

2.1.10 Коэффициент учитывающий двухстороннее нагружение

Y_А3= Y_А4 = 1 (для одностороннего нагружения)

2.1.11 Допустимые напряжения изгиба [2]

- для шестерни

- для колеса

Для нахождения межосевого расстояния принимаем коэффициент относительной ширины колес ψ _ba = 0, 4 из ряда стандартных; вспомогательный коэффициент для прямозубых K_a=490; коэффициент учитывающий неравномерность нагрузки по длине контактной линии K_Hβ = 1, 15

2.1.12 Межосевое расстояние [2]

мм.

Полученное значение a_w межосевого расстояния округляем дл ближайшего значения по ГОСТ 2185-66; принимаем a_w = 200 мм.

2.1.13 Необходимая ширина зубчатого венца

b_w₄ = a_w ∙ ψ _ba= 200 ∙ 0, 4 = 80мм.

Ширину венца шестерни принято принимать на 3…5 мм больше, чем у колеса, поэтому для шестерни b_w₃ = 85мм.

2.1.14 Нормальный модуль зубчатого колеса

m_n = (0, 01…0, 02)a_w = (0, 01…0, 02) ∙ 200 = 2…4 мм.

В соответствии с ГОСТ 9563-60 назначаем m_n = 3мм.

Предварительно принимаем угол наклона зубьев β = 10° и проверяем условие обеспечивающее двухпарное зацепление

в нашем случае и условие выполняется.

2.1.15 Определение суммарного числа зубьев

Принимаем суммарное число зубьев z_∑=131

С целью сохранения стандартных значений межосевого расстояния и модуля корректируем угол наклона зубьев:

Принимаем угол наклона зубьев β =10, 78°

2.1.16 Число зубьев колеса и шестерни

-для шестерни

-для колеса

2.1.17 Диаметры делительных окружностей зубчатых колес [2]

- для шестерни

-для колеса

2.1.18 Диаметры вершин

-для шестерни

d_a₃ = d₃ + 2m_n = 51, 91 + 6 = 57, 91мм

-для колеса

d_a₄ = d₄ + 2m_n = 342, 14+ 6 = 348, 14 мм

2.1.19 Диаметр впадин

-для шестерни

d_β₃ = d₃ + 2, 5m_n = 57, 91 - 7, 5 = 44, 41мм

-для колеса

d_β₄ = d₄+ 2, 5m_n = 342, 14 - 7, 5 = 334, 64 мм

2.1.20 Окружная скорость

м/с

Степень точности изготовления передачи 9.

2.1.21 Коэффициенты расчётной нагрузки при расчёте по контактным напряжениям и напряжениям изгиба:

Определяем коэффициенты динамичности нагрузки по таблице , , коэффициенты концентрации нагрузки для прирабатывающихся колёс принимаем , .

для прямозубых передач и .

Так как фактический коэффициент расчётной нагрузки при расчете по контактным напряжениям , принятого в проектном расчёте, то проверка по контактным напряжениям не требуется.

2.1.22 Силы, действующие в зацеплении [2]

- окружная сила

;

- радиальная сила

;

где: a = 20^о - угол зацепления

- осевая сила

2.1.23 Проверка зубьев на прочность по напряжениям изгиба

Проверку проводим для того из колёс, для которого будет меньше отношение , где Y_F – коэффициент формы зуба. Коэффициент формы зуба определяем по таблице 2.1

Таблица 2.1. Коэффициент формы зуба [2] .

Для шестерни Y_F₁ = 4, 025, .

Для колеса Y_F₂= 3, 604, .

Проверку зубьев на прочность по напряжениям изгиба проводим для зубьев колеса.

σ _F₂ = .

Прочность зубьев по напряжениям изгиба обеспечена.

2.2 Выбор материалов зубчатых колёс и термической обработки быстроходной ступени

2.2.1 Диаметр внешней делительной окружности

d_e₂ = (1, 4…1, 6)a_w = (1, 4…1, 6)·200 = 280…320 мм.

Назначаем диаметр внешней делительной окружности d_e = 315 мм.

2.2.2 Ширина венца шестерни и колеса

В соответствии со стандартным диаметром внешней делительной окружности ширину колеса и шестерни принимаем: b_w = 48 мм.

2.2.3 Диаметр внешней делительной шестерни

2.2.4 Число зубьев шестерни и колеса

Согласно рисунку 2.1 определяем число зубьев [2]

-для шестерни

z₁ = 21

Рисунок 2.1. Графики для определения чисел зубьев конической шестерни: а – прямозубой; б – с круговыми зубьями

-для колеса

z₂ = z₁·u_{1, 2} = 21·2, 4 = 50

2.2.5 Внешний окружной модуль

2.2.6 Внешнее конусное расстояние [2]

2.2.7 Угол делительного конуса шестерни

δ ₁ = 23, 87°

2.2.8 Угол делительного конуса колеса

δ ₂ = 90-23, 87 = 66, 13°

2.2.9 Среднее конусное расстояние

R_m = R_e-0, 5b_w = 170, 82-0, 5·48 = 146, 28 мм.

2.2.10 Коэффициент относительной ширины

2.2.11 Средний делительный диаметр колеса и шестерни

- для колеса

d_m₂ = (1-0, 5K_be)·d_e₂ = (1-0, 5·0, 2818)·315 = 270, 61мм.

- для шестерни

d_m₁ = (1-0, 5K_be)·d_e₂ = (1-0, 5·0, 2818)·131, 25= 112, 75мм.

2.2.12 Средний окружной модуль

2.2.13 Коэффициент учитывающий механические свойства материалов сопряженных зубчатых колес [2]

для стали Z_E = 190 МПа

2.2.14 Коэффициент учитывающий форму колес

для прямозубой передачи Z_H = 2, 5

2.2.15 Коэффициент торцевого перекрытия

2.2.16 Коэффициент учитывающий суммарную длину контактной линии

2.2.17 Окружная скорость колес на среднем диаметре

По таблице 2.1 назначаем 7-ю степень точности передачи

Таблица 2.1 Рекомендуемые степени точности зубчатых передач [2]

2.2.18 Коэффициент учитывающий распределение нагрузки между зубьями

для прямозубых передач K_Hα = 1

2.2.19 Коэффициент учитывающий неравномерность нагрузки по длине контактной линии

при НВ≤ 350 K_Hβ = 1, 06

2.2.20 Коэффициент учитывающий динамическую нагрузку

для 7-й степени точности и твердости НВ₁ или НВ₂≤ 350 принимаем K_v = 1, 15

2.2.21 Окружная сила на среднем диаметре колеса

2.2.22 Действующие контактные напряжения [2]

где: υ = 0, 85 – нагрузочный коэффициент для конических прямозубых колес;

Изготовление конических колес их материала такого же, что и для цилиндрических, экономически не обосновано, так как коническая пара будет существенно не догружена. Поэтому целесообразно принять материал для конических колес, имеющий меньшую твердость.

2.2.23 Расчетное число циклов нагружений

- для шестерни

-для колеса

2.2.24 Базовое число циклов напряжений

- для шестерни

-для колеса

2.2.25 Коэффициент долговечности

- для шестерни

-для колеса

2.2.26 Требуемый предел контактной выносливости зубьев колес

2.2.27 Требуемая твердость колеса

Назначаем для колеса Сталь 45Х улучшенную твердостью НВ 163…269

2.2.28 Расчетная контактная твердость колеса

С учетом приработки колес для шестерни назначаем Сталь 40Х улучшенную твердостью НВ 260…280

2.2.29 Расчетная контактная твердость шестерни

2.2.30 Оцениваем возможность приработки колес:

HB₁ > HB₂ + (10…15);

245 МПа > 226…231 МПа

Условия приработки выполнены

2.2.31 Допустимые контактные напряжения

- для шестерни

-для колеса

Для определения допустимых напряжений изгиба принимаем коэффициент запаса прочности S_F = 1, 7;

2.2.32 Предел выносливости зубьев на изгиб для данного материала [2]

-для шестерни

-для колеса

2.2.33 Коэффициент долговечности

-для шестерни

-для колеса

Согласно условию 1≤ Y_N≤ 4 принимаем Y_N₁= Y_N₂=1.

2.2.34 Коэффициент учитывающий двухстороннее нагружение

Y_А1= Y_А2 = 1 (для одностороннего нагружения)

2.2.35 Допустимые напряжения изгиба

- для шестерни

- для колеса

2.2.36 Коэффициент формы зуба

Коэффициент формы зуба определяем по таблице 2.1

- для шестерни

Y_F₁ =4, 01

- для колеса

Y_F₂ =3, 65

Коэффициенты Y_ε=Y_β=K_Fα=1; K_Fβ=1, 08

2.2.37 Окружная скорость

7-я степень точности

2.2.38 Коэффициент динамической нагрузки

При 7-й степени точности и окружной скорости принимаем:

K_Fv = 1, 2744

2.2.39 Проверка зубьев по напряжениям изгиба колеса

16, 67МПа<

Условие выполнено

2.2.40 Определяем силы действующие в зацеплении:

окружная сила

радиальная сила ;

осевая сила ;

где: a = 20^о - угол зацепления.

Рисунок 2.2. Цилиндрическая шестерня и тихоходный вал. Выполненно с помощью программы Компас-3D.

3. Проектный расчет валов. Выбор подшипников;

Для выбора подшипников необходимо оценить нагрузки на опоры валов. Для этого определяем положение подшипников по отношению к приложенным силам

3.1 Быстроходный вал

Так как на быстроходном валу присутствуют радиальная и осевая нагрузки, на валах конической ступени применяют радиально-упорные подшипники. Чтобы уменьшить габариты быстроходного вала по длине, подшипники устанавливаем «врастяжку». Предварительно назначаем роликовый радиально-упорный подшипник 10227309А ГОСТ 27365-87, у которого габаритные размеры d₁=45мм; D₁=100мм; b₁=25мм. Для удобства сборки ступени второй подшипник выбираем меньшего диаметра чем первый. Предварительно назначаем роликовый радиально-упорный подшипник 10227308А ГОСТ 27365-87, у которого габаритные размеры d₂=40мм; D₂=90мм; b₂=23мм

3.1.1 Диаметр выходного конца вала [2]

Окончательно назначаем диаметр выходного конца d₁=35мм=d_Дв

где: d_Дв=35мм – диаметр вала электродвигателя

Назначаем:

-диаметр под уплотнение

d_у=40мм

-диаметр под подшипник

d_П1=40мм

-диаметр под второй подшипник

d_П2=45мм

-диаметр упорного буртика

d_Б=55мм

3.1.2 Длины ступеней вала

Длины ступеней вала назначаем исходя из конструктивных размеров корпуса редуктора, формы стакана и крышки

-длина выходного конца

l_вых=64мм

-длина под первый подшипник

l_П=63мм

-длина под второй подшипник

l_П1=90мм

-длина буртика

l_Б=4мм

3.1.3 Определение радиальных реакций в подшипниках

Рисунок 3.1. Расчетная схема быстроходного вала

3.1.4 Консольная нагрузка из силового расчета привода

3.1.5 Сумма моментов всех сил относительно точки Б в горизонтальной плоскости [2]

3.1.6 Сумма моментов всех сил относительно точки Б в вертикальной

плоскости

3.1.7 Полная радиальная реакция в подшипнике Б

3.1.8 Сумма моментов всех сил относительно точки А в горизинтальной плоскости

3.1.9 Сумма моментов всех сил относительно точки А в вертикальной плоскости

3.1.10 Полная радиальная реакция в подшипнике А

3.1.11 Уравнения изгибающих моментов по участкам в горизонтальной плоскости

Участок а (0£ x £ a): ,

при x=0: ;

при x=а:

Участок b (0£ x £ b): ,

при x=0: ;

приx=b: .

3.1.12 Уравнения изгибающих моментов по участкам в вертикальной плоскости

Участок а (0£ x £ a): .

при x=0: ;

при x=а: .

Участок b (0£ x £ б): ,

при x=0: ;

при x=b:

Участок c (0£ x £ в): ,

при x=0: при x=c: .

3.1.13 Суммарный изгибающий момент

Участок а

Участок б

Участок с

Рисунок 3.2. Построение эпюр для быстроходного вала

3.2 Промежуточный вал

Предварительно назначаем роликовый радиально-упорный подшипник 1027307А ГОСТ 27365-87, у которого габаритные размеры d₁=35мм; D₁=80мм; b₁=21мм.

3.2.1 Диаметр выходного конца вала

Окончательно назначаем диаметр выходного конца d₂=35мм

Назначаем:

-диаметр под подшипник

d_П1=35мм

-диаметр под зубчатое колесо

d_К2=40мм

-диаметр упорного буртика

d_Б=46мм

3.2.2 Длины ступеней вала

Длины ступеней вала назначаем исходя из конструктивных размеров корпуса редуктора, формы стакана и крышки

-длины под подшипник

l_П1=35мм

-длина под колесо

l_К1=80мм

-длина буртика

l_Б=5мм

3.2.3 Определение радиальных реакций в подшипниках

Рисунок 3.3. Расчетная схема промежуточного вала

3.2.4 Сумма моментов всех сил относительно точки Б в вертикальной плоскости

: ,

3.2.5 Сумма моментов всех сил относительно точки Б в горизонтальной плоскости

: ,

3.2.6 Полная радиальная реакция в подшипнике Б

3.2.7 Сумма моментов всех сил относительно точки А в горизонтальной

плоскости

3.2.8 Сумма моментов всех сил относительно точки А в вертикальной плоскости

: ,

3.2.9 Уравнения изгибающих моментов по участкам в горизонтальной плоскости

Участок а (0£ x £ а): ,

при x=0: ;

при x=а: .

Участок б (0£ x £ б): ,

при x=0: ;

при x=б: .

Участок в (0£ x £ в): ,

при x=0: ;

при x=в:

3.2.10 Уравнения изгибающих моментов по участкам в вертикальной плоскости

Участок а (0£ x £ а): .

при x=0: ;

при x=а:

Участок б (0£ x £ б): ,

при x=0: ;

при x=б: Участок в (0£ x £ в): ,

при x=0:

при x=в

3.2.11 Суммарный изгибающий момент

Участок а

Участок б

Участок с

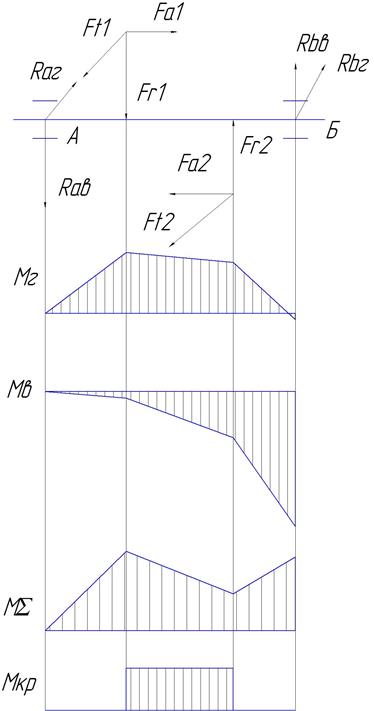
Рисунок 3.4 Построение эпюр для промежуточного вала

3.3 Тихоходный вал

Предварительно назначаем роликовый радиально-упорный подшипник 1027311А ГОСТ 27365-87, у которого габаритные размеры d₁=55мм; D₁=120мм; b₁=29мм.

3.3.1 Диаметр выходного конца вала

Окончательно назначаем диаметр выходного конца d₂=52мм

Назначаем:

диаметр под уплотнение

d_У1=55мм

-диаметр под подшипник

d_П1=55мм

-диаметр под зубчатое колесо

d_К2=60мм

-диаметр упорного буртика

d_Б=65мм

3.3.2 Длины ступеней вала

Длины ступеней вала назначаем исходя из конструктивных размеров корпуса редуктора, формы стакана и крышки

-длина под подшипник

l_П1=18мм

-длина под уплотнение

l_У1=32мм

-длина под колесо

l_К1=52мм

-длина буртика

l_Б=45мм

3.3.3 Определение радиальных реакций в подшипниках

Рисунок 3.5. Расчетная схема тихоходного вала

3.3.3 Сумма моментов всех сил относительно точки Б в горизонтальной плоскости

: ,

3.3.4 Сумма моментов всех сил относительно точки Б в вертикальной плоскости:

: ,

3.3.5 Полная реакция в подшипнике А

3.3.6 Сумма моментов всех сил относительно точки А в горизонтальной плоскости

: ,

3.3.7 Сумма моментов всех сил относительно точки А в вертикальной плоскости:

: ,

;

3.3.8 Полная реакция в подшипнике В

3.3.9 Уравнения изгибающих моментов по участкам в горизонтальной плоскости.

Участок а (0£ x £ a): .

Участок б (0£ x £ б): ,

при x=0: ;

при x=b: .

Участок в (0£ x £ в): ,

при x=0: ;

при x=в: .

3.3.10 Уравнения изгибающих моментов по участкам в вертикальной плоскости.

Участок а (0£ x £ a): .

при x=0: ;

при x=а: .

Участок б (0£ x £ б): ,

при x=0: ;

при x=б:

Участок в (0£ x £ в): ,

при x=0: ;

при x=в:

3.3.11 Суммарный изгибающий момент

Участок а

Участок б

Участок с

Рисунок 3.6 Построение эпюр для тихоходного вала

⇐ Предыдущая 5 6 7 8 9 10 11 12 1314