Метод проекций. Проецирование на одну и две плоскости проекций

⇐ ПредыдущаяСтр 3 из 5Следующая ⇒

Для того чтобы грамотно составлять и читать чертежи надо знать не только правила их оформления, но и правила построения изображения предметов.

Процесс получения изображения на плоскости называется проецированием. Как же получаются проекции?

Возьмем в пространстве произвольную точку А и какую-нибудь плоскость Н. Проведем через точку А прямую до пересечения с плоскостью Н, полученная точка а пересечения линии и плоскости есть проекция точки А. Плоскость, на которой получается проекция, называется плоскостью проекций. Прямая Аа называется проецирующим лучом (рис. 35).

Рис. 35. Проецирование луча на плоскость

Следовательно, чтобы построить проекцию какой-либо фигуры на плоскости, необходимо через точки этой фигуры провести воображаемые проецирующие лучи до их пересечения с плоскостью. Слово проекция – латинское, в переводе на русский язык означает «отбрасывать вперед».

Точки, взятые на предмете обозначают прописными буквами А, В, С, а их проекции – строчными а, в, с.

Если проецирующие лучи исходят из одной точки, такое проецирование называется центральным. Точка S, из которой исходят лучи, называется центральной (рис. 36).

Рис. 36. Центральное проецирование

Примерами центральной проекции являются фотографии, кинокадры, тени, отброшенные от предмета лучами электрической лампочки.

Если проецирующие лучи параллельны друг другу, то проецирование называется параллельным, а полученная проекция – параллельной. Примером параллельной проекции можно условно считать солнечные тени от предметов.

При параллельном проецировании все лучи падают на плоскость проекций под одинаковым углом. Если это любой острый угол, то проецирование называется косоугольным (рис. 37).

Рис. 37. Параллельное проецирование

В том случае, когда проецирующие лучи перпендикулярны плоскости проекции, проецирование называется прямоугольным. Полученная при этом проекция называется прямоугольной (рис. 38).

Рис. 38. Прямоугольное проецирование

Из всех рассмотренных способов проецирования в основе построения изображения лежит способ прямоугольного проецирования, так как полученное изображение на плоскости проецируется без искажения.

В пространстве плоскость проекций может располагаться как угодно: вертикально, горизонтально, наклонно.

Чтобы получить проекцию предмета на плоскости, его располагают параллельно этой плоскости и через каждую вершину проводят лучи перпендикулярно этой плоскости проекций.

Рассмотрим построение проекции предмета, изображенного на рис. 39 на плоскость.

Рис. 39. Проецирование на фронтальную плоскость проекций

Выберем вертикальную плоскость проекции, расположенную перед зрителем. Эту плоскость называют фронтальной (от французского слова « фронталь », что означает « лицом к зрителю » и обозначают буквой V(ве).

Мысленно рассмотрим предмет параллельно фронтальной плоскости и через все точки проведем проецирующие лучи перпендикулярно плоскости V. Отметим точки пересечения лучей с плоскостью и соединим прямыми, а точки окружности - кривой линией. Мы получим проекцию предмета на плоскости, которую называют фронтальной проекцией (рис. 40).

Рис. 40. Фронтальная проекция

По полученной проекции можно судить лишь о двух измерениях – высоте, длине и о диаметре отверстия.

А какова ширина предмета? Пользуясь полученной проекцией, мы этого сказать не можем. Значит, одна проекция не выявляет третьего измерения предмета, кроме того, одна проекция не всегда определяет геометрическую форму предмета (рис. 41).

Рис. 41. Неоднозначность выявления формы предмета одной проекцией:

а – фронтальная проекция; б, в – возможная форма предмета

Фронтальная проекция, показанная на рис. 42, соответствует всем деталям.

Рис. 42. Проекции на фронтальную и горизонтальные плоскости проекций

Для того, чтобы определить форму предмета необходимо построить вторую проекцию на плоскость, которая называется горизонтальной плоскостью и обозначается буквой Н (аш). Проекция предмета на эту плоскость называется горизонтальной проекцией.

Горизонтальная плоскость расположена под углом 90⁰к фронтальной. Плоскость V и Н пересекаются по оси ОХ, (О – точка пересечения осей), которая называется осью проекции. По горизонтальной проекции можно определить длину и ширину детали.

Изображения предмета выполняются в одной плоскости, поэтому для получения чертежа предмета обе плоскости совмещают в одну, развернув горизонтальную плоскость вокруг оси ОХ вниз на 90⁰ так, чтобы она совпала с фронтальной плоскостью (см. рис. 42).

Границы плоскости на чертеже не показывают, а также ось проекций, если в том нет необходимости (рис. 43).

Рис. 43. Расположение фронтальной и горизонтальной проекции на чертеже

Горизонтальная проекция располагается строго под фронтальной проекцией. Расположение между проекциями выбирают произвольно, предусматривая при этом место для нанесения размеров.

2.2. Проецирование на три плоскости проекций. Виды.
Расположение видов на чертеже

Зачастую даже две проекции детали не дают полного представления о ее геометрической форме (рис. 44).

Рис. 44. Примеры неоднозначного выявления формы детали с помощью двух проекций

Данному чертежу соответствуют несколько деталей, поэтому возникает необходимость построения третьей проекции на плоскость. Эту плоскость располагают перпендикулярно плоскости проекции V и Н.

Третью плоскость проекций называют профильной, а полученную на ней проекцию – профильной проекцией предмета.

Обозначается профильная плоскость буквой W (дубль - ве). Профильная плоскость проекций вертикальная, в пересечении с плоскостью Н она образует ось ОY, а с плоскостью V – ось ОZ. Профильная проекция располагается справа от фронтальной проекции на одной с ней высоте
(рис. 45 а, б) Плоскости V, H, W образуют трехгранный угол. Проецируемый предмет поместим в пространство трехгранного угла и через все точки предмета проведем проецирующие лучи до пересечения с плоскостями проекций. Соединим точки пересечения прямыми или кривыми линиями, полученные фигуры будут проекциями предмета на плоскостях V, Н, W (рис. 45, б).

Рис. 45. Проекции предмета на три плоскости проекций V, Н, W

Проецируемый предмет помещен в пространство трехгранного угла а) проекции предмета на плоскостях V, Н, W.

Для получения чертежа предмета плоскости V, H, W совмещают в одну плоскость, развернув плоскость W на 90⁰ вправо, а Н – на 90⁰ вниз (рис. 46, б). Границы плоскостей, оси проекций и проецирующие лучи на чертеже не показывают (рис. 46, в, г).

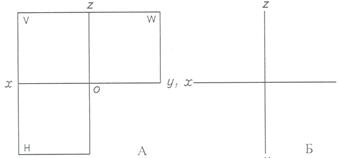
Рис. 46. Расположение плоскостей проекций и осей на плоскости:

а – трехгранный угол, образованный плоскостями V, H, W; б – процесс совмещения плоскостей
3-хгранного угла с плоскостью чертежного листа; в - расположение плоскостей проекции на плоскости чертежного листа; г – расположение осей на плоскости чертежного листа

Рассмотрев процесс проецирования на три плоскости проекций, можно сделать вывод, что проецирование проводят в следующей последовательности:

- предмет в системе плоскостей проекций V, H, W;

- проецирующие лучи перпендикулярны V и направляются спереди, получается фронтальная проекция;

- лучи перпендикулярны Н и направляются сверху, получается горизонтальная проекция;

- лучи перпендикулярны W и направляются слева, получается профильная проекция;

- совмещаем V, H, W в одну плоскость.

Чертеж, состоящий из нескольких прямоугольных проекций называют комплексным чертежом или чертежом в системе прямоугольных проекций.

Если чертеж построен с осями координат, он называется осным чертежом, а если без осей, он называется безосным. Все проекции на чертеже находятся в проекционной связи, которая осуществляется посредством линий связи (рис. 47).

Рис. 47. Построение профильной проекции предмета по двум данным

Вам уже известно, что правила оформления и построения чертежей установлены стандартами ЕСКД. Один из стандартов этой системы устанавливает правила изображения предметов на чертежах, в нем даны определения различных изображений, применяемых при выполнении чертежей.

На технических чертежах проекции на плоскостях называют видами.

Вид – это изображение обращенной к наблюдателю видимой части предмета. В том же стандарте говорится, что предмет располагают относительно фронтальной плоскости так, чтобы изображение на ней давало наиболее полное представление о форме и размерах предмета. Поэтому изображение на фронтальной плоскости называют главным видом или видом спереди.

Изображение на горизонтальной плоскости называют видом сверху.

Изображение на профильной плоскости называют видом слева (рис. 48).

Рис. 48. Расположение на плоскостях проекций видов детали

Вид сверху располагается под главным видом, а справа от главного вида и на одной с ним высоте – вид слева.

Невидимые части предмета на видах показывают штриховыми линиями.

Количество видов на чертеже должно быть минимальным, но достаточным для того, чтобы понять форму изображенного предмета. Виды также как и проекции располагаются в одной проекционной связи друг с другом.

2.3. Геометрические тела и их проекции.
Проекции вершин, ребер, граней на плоскости.
Проекции группы геометрических тел

Формы деталей, встречающихся в технике, представляют собой сочетание различных геометрических тел или их частей.

Чтобы научиться представлять форму предмета по чертежу, нужно знать, как изображаются на чертежах геометрические тела.

Геометрическое тело – это замкнутая часть пространства, ограниченная плоскостями или кривыми поверхностями.

Все геометрические тела подразделяются на многогранники (куб, параллелепипед, призмы, пирамиды) и тела вращения (цилиндр, шар, конус).

Геометрические тела состоят из определенных элементов – вершины, ребра, грани (рис. 49).

Рис. 49. Элементы геометрических тел

Ребра, расположенные перпендикулярно плоскостям проекции, проецируются на них в точку.

Ребра, расположенные параллельно плоскостям проекций, проецируются на них в натуральную величину.

Грани, перпендикулярные плоскостям проекций, проецируются в отрезки прямой.

Грани, параллельные плоскостям проекций, проецируются в натуральную величину.

Грани и ребра, наклоненные к плоскостям проекций, проецируются на них с искажением.

Строя чертеж, надо четко представлять, как изобразится на нем каждая вершина, ребро и грань предмета. Следует помнить, что каждый вид - это изображение всего предмета, а не одной его стороны. Разница заключается лишь в том, что одни грани проецируется в истинную фигуру, другие - в отрезки прямых (рис. 50).

Рис. 50. Проецирование граней и ребер геометрических тел на плоскости проекций

Проекциями геометрических тел являются плоские геометрические фигуры.

Рассмотрим основные геометрические тела и их проекции.

Проекциями куба являются три равных квадрата, призмы – два прямоугольника и многоугольник; пирамиды - два треугольника и многоугольник; усеченной пирамиды – две трапеции и многоугольник; конуса – два треугольника и окружность; усеченного конуса - две трапеции и окружность; шара – три окружности, цилиндра – два прямоугольника и окружность (рис. 51).

а - четырехгранная призма б - трехгранная призма в - четырехгранная пирамида

г - 4-х гранная усеченная пирамида д - конус

е - конус ж - шар

Рис. 51. Проекции геометрических тел на плоскости проекций

Чтобы научиться быстро читать чертежи, надо уметь находить проекции геометрических тел и определять их взаимное расположение.

Рассмотрим чертеж группы геометрических тел (рис. 52).

Рис. 52. Проекция группы геометрических тел на три плоскости проекций

Группа состоит из трех геометрических тел. Первое геометрическое тело на плоскостях V и W изображено треугольником, а на плоскости Н – кругом. Такие проекции имеет только конус. Второе геометрическое тело на плоскостях Н и W представлено двумя прямоугольниками, а на фронтальной плоскости - окружностью. Такие проекции имеет цилиндр. Третье геометрическое тело на всех плоскостях представлено прямоугольниками, значит это параллелепипед.

Таким образом можно сделать вывод, что на чертеже представлена группа геометрических тел, состоящая из конуса, цилиндра и параллелепипеда. Чтобы определить, какое из геометрических тел находится ближе к нам, надо рассмотреть вид сверху. На основании анализа приходим к выводу, что ближе к нам находятся параллелепипед и цилиндр.

2.4. Анализ геометрической формы предмета.
Проекции точек, лежащих на поверхности геометрических тел и предметов

Вы уже знаете, что окружающие нас предметы, детали машин и механизмов имеют форму геометрических тел или их сочетания.

Рассмотрим рис. 53. Здесь изображены различные детали, одни простой формы, другие более сложной формы.

Как же определить форму предмета по чертежу? Для этого сложную по форме деталь мысленно расчленяют на отдельные части, имеющие форму геометрических тел.

Рис. 53. Детали состоящие из сочетания простых геометрических тел

Например на рис. 54. дано изображение детали. Она слагается из параллелепипеда, двух полуцилиндров и усеченного конуса. В детали имеется отверстие цилиндрической формы.

Рис. 54. Анализ геометрической формы опоры:

а – изображение опоры; б - составные части опоры

Мысленное расчленение предмета на составляющие его геометрические тела называется анализом геометрической формы.

Любая точка на изображении геометрических тел является проекцией того или иного элемента – вершины, ребра, грани, кривой поверхности.

Значит, изображение любого геометрического тела сводится к изображению его вершин, ребер, граней и кривых поверхностей.

Рассмотрим процесс построения проекций точек на чертежах геометрических тел и деталей.

Работа осуществляется в следующей последовательности:

- устанавливают грань многогранника или часть поверхности вращения, на которой задана проекция точки, и определяют видимость этой части геометрического тела на всех видах (рис. 55, а);

- через заданную проекцию точки проводят проекцию вспомогательной прямой, строят ее и проекцию точки на том виде, где проекция геометрического тела совместилась с проекцией его основания (рис. 55, б);

- строят проекцию вспомогательной прямой и находят на ней искомую проекцию заданной точки (рис. 55, в).

в)

б)

а)

Рис. 55. Пример построения проекции точки на заданной поверхности геометрических тел

Если нужно построить проекции точек на поверхности предмета, представленной чертежом, то:

- проводят анализ геометрической формы;

- устанавливают геометрические тела, на поверхности которых заданы точки;

- определяют проекцию точек поочередно на каждом геометрическом теле.

На детали точки обозначаются прописными буквами А, В, С, а их проекции - строчными, например, проекции точки А на плоскостях Н-а, V-а^′, W-а″, невидимые точки заключаются в скобки, например, V-(а′ ), Н-(а), W-(а″ ).

2.5. Порядок чтения и построения чертежа детали.
Построение третьего вида по двум заданным

Чтобы познакомиться с устройством какого-либо изделия, необходимо прочитать его чертеж.

Прочитать чертеж - это значит представить по плоским изображениям чертежа объемную форму изображенного на нем предмета.

Чертеж читают в следующей последовательности:

- прочитать основную надпись чертежа, из нее можно узнать название детали, наименование материала, из которого ее изготовляют, масштаб изображения;

- определить, какие виды детали даны на чертеже;

- определить геометрическую форму детали;

- определить габаритные размеры детали и ее элементов;

Рассмотрим пример чтения чертежа детали (рис. 56).

Рис. 56. Чертеж направляющей

Вопросы к чертежу

1. Как называется деталь?

2. Из какого материала ее изготовляют?

3. В каком масштабе выполнен чертеж?

4. Какие виды даны на чертеже?

5. Сочетанием каких геометрических тел определяется форма детали?

6. Чему равны габаритные размеры?

Ответы на вопросы

1. Деталь называется «направляющая».

2. Изготовляют деталь из стали.

3. Масштаб 1: 1.

4. На чертеже даны два вида; главный вид и вид слева.

5. Выделив части детали, рассмотрим их слева направо, сопоставляя оба вида.

Крайняя левая часть на главном виде имеет форму прямоугольника, а на виде слева – окружность. Значит это цилиндр.

Вторая слева часть на главном виде – трапеция, на виде слева – две окружности, это усеченный конус. Третья часть на главном виде показана прямоугольником, а на виде слева – окружность, значит это цилиндр. Четвертая часть на главном виде – прямоугольник, а на виде слева – шестиугольник, значит это шестигранная призма. Крайняя слева часть на главном виде – прямоугольник, а на виде слева - окружность, это цилиндр. Штриховые линии на главном виде и окружность ø 20 на виде слева говорит о том, что деталь имеет сквозное цилиндрическое отверстие.

6. Габаритные размеры детали 160х90х90.

Многие технические детали имеют разнообразные технологические и конструктивные элементы, которые имеют свои названия (рис. 57).

Отверстия

Пазы

Рис. 57. Название конструктивных элементов деталей

Отверстие – сквозной или глухой элемент детали, имеющий форму геометрического тела.

Паз – узкая щель или выемка.

Вырез – удаление части детали двумя или большим количеством плоскостей.

Срез – удаление части детали одной плоскостью.

Ребро (ребро жесткости) – тонкая стенка, предназначенная для усиления жесткости конструкции.

Прежде чем приступить к построению изображений, надо четко представить геометрическую форму детали.

Рассмотрим последовательность построения видов на чертеже (рис. 58).

Рис. 58. Наглядное изображение опоры

Общая форма предмета, изображенного на рис. 58 – параллелепипед. В нем сделаны прямоугольные вырезы и вырез в виде треугольной призмы. Изображать деталь начнем с ее общей формы – параллелепипеда (рис. 59).

Рис. 59. Пример последовательности построения видов детали:

а – изображение общих видов детали; б – построение вырезов; в – нанесение размеров

Спроецировав параллелепипед на плоскости V, H, W, получим прямоугольники на всех трех плоскостях (рис. 59, а).

Все построения выполняются сначала тонкими линиями. Поскольку деталь симметрична, на главном виде и виде сверху нанесем оси симметрии.

Теперь покажем вырезы. Их целесообразнее показать сначала на главном виде.

Для этого надо отложить по 12 мм влево и вправо от оси симметрии и провести через полученные точки вертикальные линии. Затем на расстоянии 14 мм от верхней границы проводим отрезки горизонтальных прямых (рис. 59, б).

Построим проекции этих вырезов на других видах. Это можно сделать при помощи линий связи. После этого на видах сверху и слева нужно показать отрезки, ограничивающие проекции видов.

Далее также с помощью линий проекционной связи строят проекции вертикального паза, и наклонного среза. Те элементы, которые на данной проекции не видимы, проводят штриховыми линиями.

В заключении обводят чертеж и наносят размеры (рис. 59, в).

В черчении довольно часто встречаются задачи, связанные с построением по двум заданным видам третьего.

Рассмотрим последовательность построения третьего вида по двум заданным (рис. 60).

Рис. 60. Чертеж бруска с вырезом

На рис. 60 вы видите изображение бруска с вырезом. Даны два вида: спереди и сверху, требуется построить вид слева. Для этого необходимо сначала представить форму изображенной детали. Сопоставив виды, определяем, что брусок имеет форму параллелепипеда размером 10х35х20 мм. В параллелепипеде сделан вырез прямоугольной формы размером 12х12х10 мм.

На виде спереди с помощью линий связи проводим две горизонтальные линии, одну на уровне нижнего основания параллелепипеда, другую – на уровне верхнего основания. Эти линии ограничивают высоту вида слева. В любом месте между горизонтальными линиями проводим вертикальную линию (рис. 61).

а)

г)

в)

б)

Рис. 61. Последовательность построения третьей проекции

Она будет проекцией задней грани бруска на профильную плоскость проекций (рис. 61, а). От нее вправо отложим отрезок, равный 20 мм, т.е. ширину бруска, и проведем еще одну вертикальную линию – проекцию передней грани (рис. 61, б).

Покажем теперь на виде слева вырез в детали. Для этого отложим влево от правой вертикальной линии, являющейся проекцией передней грани бруска, отрезок 12 мм и проведем еще одну вертикальную линию (рис. 61, в).

После этого удаляем все вспомогательные линии построения и обводим чертеж (рис. 61, г).

⇐ Предыдущая 1 234 5 Следующая ⇒