
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Интегральное исчисление функции одной переменнойСтр 1 из 3Следующая ⇒
Глава 5. Интегральное исчисление функции одной переменной Наряду с понятиями производной и дифференциала возникло и тесно связанное с ними понятие интеграла. Понятие интеграла – одно из важнейших в математическом анализе. Первообразная и неопределенный интеграл Рассмотрим задачу: дана функция Функция Пример 5.1 Дана функция Аналогично, так как Если для данной функции существует первообразная, то она не единственная. В самом деле, для данной функции, например Теорема. Любые две первообразные Неопределенным интегралом от данной функции Например, для функции
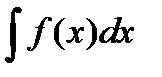 , где спереди стоит символ интеграла, а , где спереди стоит символ интеграла, а 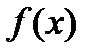 называется подынтегральной функцией, а называется подынтегральной функцией, а 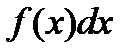 подынтегральным выражением ( подынтегральным выражением ( 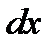 означает дифференциал аргумента). означает дифференциал аргумента). По определению Процесс нахождения неопределенного интеграла данной функции называется интегрированием этой функции.
Свойства неопределенного интеграла 1.Производная неопределенного интеграла равна подынтегральной функции:
2.Дифференциал неопределенного интеграла равен подынтегральному выражению:
3.Неопределенный интеграл от дифференциала функции
Дифференцирование и интегрирование функций являются взаимно обратными операциями. Последовательное применение операций дифференцирования и интегрирования
4.Постоянный множитель С можно выносить за знак неопределенного интеграла:
5.Неопределенный интеграл алгебраической суммы конечного числа функций равен алгебраической сумме интегралов слагаемых Неопределенный интеграл не зависит от обозначения переменной интегрирования. Он зависит только от вида подынтегральной функции.
6. Если
Таблица основных неопределенных интегралов Ниже приводятся простейшие интегралы, часть которых получается непосредственно из таблицы производных, если прочитать ее справа налево. Другую часть интегралов легко проверить путем дифференцирования правой части. 1) 2) 3) 4) 5) 6) 7) 8)
Существует справочная литература, где число табличных интегралов насчитывает многие сотни (например, «Таблицы неопределенных интегралов», Бычков Ю.А., Маричев О.И., Прудников А.П., М.: Физматлит, 2003.) Существуют и так называемые «неподдающиеся» интегралы, не имеющие первообразной, выраженной через элементарные функции, например,
Основные методы интегрирования Процесс интегрирования состоит в умении привести интеграл от данной функции к одному или нескольким табличным интегралам с использованием математических преобразований и свойств неопределенного интеграла. Мы рассмотрим три основных метода:
Определенный интеграл Определенный интеграл связан с непосредственным приложением интегрального исчисления к решению прикладных задач. Введем понятие определенного интеграла и познакомимся с его свойствами и методами вычисления.
Формулы прямоугольников Заменим площадь каждой частичной криволинейной трапеции площадью прямоугольника с основанием Тогда приближенное значение площади фигуры Иначе говоря, получим формулу приближенного интегрирования
Если же в качестве высот прямоугольников возьмем их правые ординаты, то площадь фигуры выразится суммой
что дает аналогичную формулу
Формулы (3.35) и (3.36) называются формулами правых и левых прямоугольников. Иногда используетсяформула средних прямоугольников:
Также существуют аналогичные формулы: формула трапеций, формула парабол (формула Симпсона). Некоторые экономические приложения определенных интегралов. Пример. Пусть эмпирическим путем было установлено, что производительность труда р в течение рабочего дня меняется по закону:
Найти дневную выработку за 8 час. рабочего дня. Решение. Дневная выработка есть определенный интеграл от производительности труда за данный промежуток времени:
Итак, дневная выработка за 8 час. рабочего дня составила 38, 4С единиц.
Вопросы для самопроверки
Упражнения и задачи
Глава 5. Интегральное исчисление функции одной переменной Наряду с понятиями производной и дифференциала возникло и тесно связанное с ними понятие интеграла. Понятие интеграла – одно из важнейших в математическом анализе. Популярное:
|
Последнее изменение этой страницы: 2016-03-25; Просмотров: 573; Нарушение авторского права страницы