
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Вычисление объемов тел вращения ⇐ ПредыдущаяСтр 3 из 3
Рассмотрим тело, образованное вращением вокруг оси
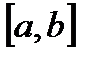  произвольно на произвольно на 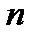 частей. Возьмем частичный отрезок частей. Возьмем частичный отрезок 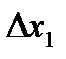 , выберем на нем произвольную точку , выберем на нем произвольную точку 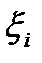 . В точках . В точках 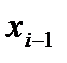 и и 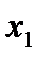 восставим перпендикуляры и построим элементарный прямоугольник высотою восставим перпендикуляры и построим элементарный прямоугольник высотою 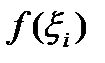 с основанием с основанием 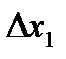 . В результате вращения этого прямоугольника вокруг оси . В результате вращения этого прямоугольника вокруг оси 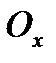 получится элементарное цилиндрическое тело, радиус которого получится элементарное цилиндрическое тело, радиус которого 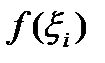 , а высота , а высота 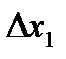 . Объем такого цилиндрического тела равен . Объем такого цилиндрического тела равен 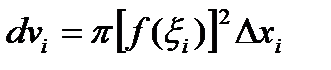 , а сумма всех , а сумма всех 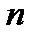 элементарных цилиндрических тел дает интегральную сумму элементарных цилиндрических тел дает интегральную сумму
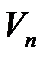 для непрерывной на отрезке для непрерывной на отрезке 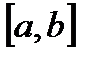 функции при функции при 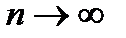 и и 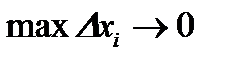 имеет предел. Его и называют объемом тела вращения вокруг координатной оси имеет предел. Его и называют объемом тела вращения вокруг координатной оси 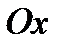 , то есть , то есть
Аналогично, объем тела вращения вокруг оси
Если вокруг оси
Пример 3.43. Найти объем тора, образованного вращением круга Решение. Круг верхней и нижней По формуле (3.33) получим
Употреблена подстановка
Определенные интегралы применяются также при вычислении центра тяжести плоских фигур, инерционных моментов вращающихся тел и др.
Приближенное вычисление определенных интегралов Мы уже знаем, что первообразные некоторых функций не могут быть выражены в конечном виде через элементарные функции. Вычисление определенных интегралов от таких функций возможно с помощью приближенных методов, которые целесообразно применять и в случаях интегрируемости функции в конечном виде, когда отыскание первообразной требует сложных выкладок. Формулы приближенного вычисления определенного интеграла связаны с геометрическим решением задачи о нахождении площади криволинейной трапеции.
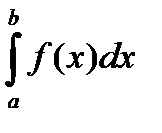 . Рассмотрим площадь криволинейной трапеции . Рассмотрим площадь криволинейной трапеции  (рис. 3.27) как геометрическое представление заданного интеграла и будем искать способы приближенного вычисления этой площади. (рис. 3.27) как геометрическое представление заданного интеграла и будем искать способы приближенного вычисления этой площади.
Разделим отрезок Из точек деления отрезка
Площадь криволинейной трапеции Формулы прямоугольников Заменим площадь каждой частичной криволинейной трапеции площадью прямоугольника с основанием Тогда приближенное значение площади фигуры Иначе говоря, получим формулу приближенного интегрирования
Если же в качестве высот прямоугольников возьмем их правые ординаты, то площадь фигуры выразится суммой
что дает аналогичную формулу
Формулы (3.35) и (3.36) называются формулами правых и левых прямоугольников. Иногда используетсяформула средних прямоугольников:
Также существуют аналогичные формулы: формула трапеций, формула парабол (формула Симпсона). Некоторые экономические приложения определенных интегралов. Пример. Пусть эмпирическим путем было установлено, что производительность труда р в течение рабочего дня меняется по закону:
Найти дневную выработку за 8 час. рабочего дня. Решение. Дневная выработка есть определенный интеграл от производительности труда за данный промежуток времени:
Итак, дневная выработка за 8 час. рабочего дня составила 38, 4С единиц.
Вопросы для самопроверки
Упражнения и задачи
Популярное:
|
Последнее изменение этой страницы: 2016-03-25; Просмотров: 799; Нарушение авторского права страницы