Оценка качества уравнения парной линейной регрессии на основе критерия Фишера.

Оценка качества уравнения парной линейной регрессии на основе критерия Фишера.

Оценка значимости уравнения регрессии в целом дается с помощью - критерия Фишера. Здесь важно определить число степеней свободы.

Любая сумма квадратов отклонений связана с числом степеней свободы , т.е. с числом свободы независимого варьирования признака. Число степеней свободы связано с числом единиц совокупности и с числом определяемых по ней констант. Существует равенство между числом степеней свободы общей, объясненной (регрессионной, факторной) и остаточной суммами квадратов. Число степеней свободы при линейной регрессии составляет . Число степеней свободы для общей суммы квадратов определяется числом единиц, и поскольку используется средняя, вычисленная по данным выборки, то теряется одна степень свободы, т.е. Итак, справедливы два равенства:

Разделив каждую сумму квадратов на соответствующее число степеней свободы, получится средний квадрат отклонений или дисперсия на одну степень свободы 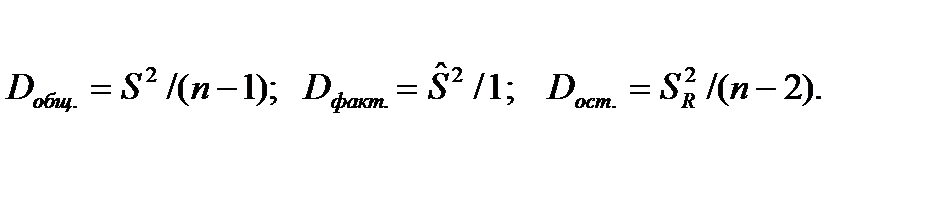Сопоставляя факторную (регрессионную, объясненную) и остаточную дисперсии в расчете на одну степень свободы, получится величина - отношения, т.е. - критерий Фишера:

- статистика используется для проверки нулевой гипотезы

Если нулевая гипотеза справедлива, то факторная и остаточная дисперсии не отличаются друг от друга. Если не справедлива, то факторная дисперсия превышает остаточную в несколько раз. Английским статистиком Снедекором разработаны таблицы критических значений - отношений при разных уровнях значимости нулевой гипотезы и различном числе степеней свободы. Табличное значение - критерия – это максимальная величина отношения дисперсий, которая может иметь место при случайном расхождении их для данного уровня вероятности наличия нулевой гипотезы. Вычисленное значение - отношения признается достоверным (отличным от единицы), если оно больше табличного. В этом случае нулевая гипотеза об отсутствии связи признаков отклоняется и делается вывод о существенности этой связи:

Если же величина окажется меньше табличной, то вероятность нулевой гипотезы выше заданного уровня (например, 0, 5 или 0, 1 или 0, 01) и она не может быть отклонена без риска сделать неправильный вывод о наличии связи. В этом случае уравнение регрессии считается статистически незначимым:

Величина -критерия связана с коэффициентом детерминации (или ). Факторную (регрессионную, объясненную) сумму квадратов можно представить как

а остаточную сумму квадратов – как

Тогда значение -критерия в соответствии (2.13) можно выразить так:

 

Оценка тесноты связи между изучаемыми явлениями с помощью индекса корреляции для нелинейной регрессии.

Уравнение нелинейной регрессии, так же как и в линейной зависимости, дополняется показателем корреляции, а именно индексом корреляции ( )

, (2.27)

где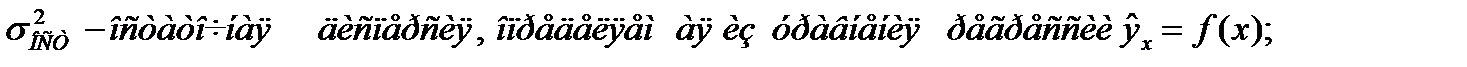

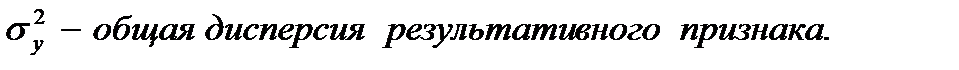
Поскольку 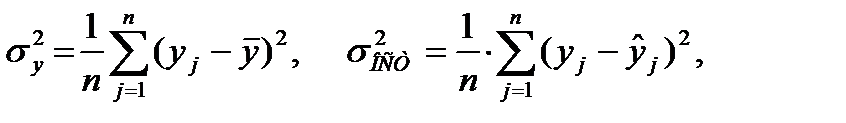индекс корреляции можно выразить как

(2.28)

Величина данного показателя находится в границах: ; чем ближе к единице, тем теснее связь рассматриваемых признаков, тем более надежно найденное уравнение регрессии.

 

Функции, используемые при построении линии тренда.

 

 

 

Полиномиальные модели тренда. Точечный и интервальный прогноз в полиномиальной модели тренда.

Оптимизационная задача составления оптимальной производственной программы предприятия.

Предприятие выпускает несколько видов продукции , имея ограниченный запас ресурсов bi, . Известны нормы затрат ресурса i на производство единицы продукции j - a_ij. Требуется найти такой план производства продукции, который обеспечивает максимум эффекта от выпуска (максимум выручки от реализации, минимум затрат), если p_j − эффективность единицы продукции (например, цена).

x_j – объем производства продукции j-го вида ,

Базовая модель задачи оптимизации производственной программы выглядит следующим образом:

- максимизируется выручка от реализации

- при ограничениях на запас i-го ресурса

- при неотрицательности переменных

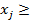0,

 

Методы и модели теории игр в экономике. Основные понятия: стратегии, платежная матрица, цена игра, нижняя и верхняя цены игры.

Оценка качества уравнения парной линейной регрессии на основе критерия Фишера.

Оценка значимости уравнения регрессии в целом дается с помощью - критерия Фишера. Здесь важно определить число степеней свободы.

Любая сумма квадратов отклонений связана с числом степеней свободы , т.е. с числом свободы независимого варьирования признака. Число степеней свободы связано с числом единиц совокупности и с числом определяемых по ней констант. Существует равенство между числом степеней свободы общей, объясненной (регрессионной, факторной) и остаточной суммами квадратов. Число степеней свободы при линейной регрессии составляет . Число степеней свободы для общей суммы квадратов определяется числом единиц, и поскольку используется средняя, вычисленная по данным выборки, то теряется одна степень свободы, т.е. Итак, справедливы два равенства:

Разделив каждую сумму квадратов на соответствующее число степеней свободы, получится средний квадрат отклонений или дисперсия на одну степень свободы 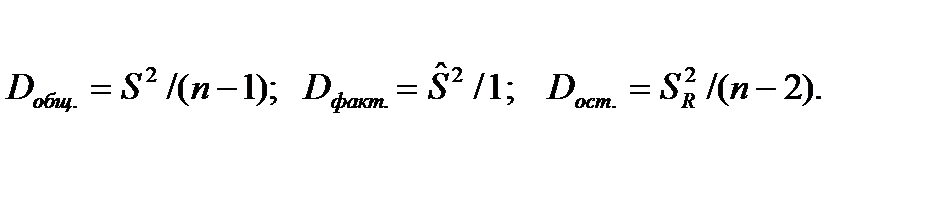Сопоставляя факторную (регрессионную, объясненную) и остаточную дисперсии в расчете на одну степень свободы, получится величина - отношения, т.е. - критерий Фишера:

- статистика используется для проверки нулевой гипотезы

Если нулевая гипотеза справедлива, то факторная и остаточная дисперсии не отличаются друг от друга. Если не справедлива, то факторная дисперсия превышает остаточную в несколько раз. Английским статистиком Снедекором разработаны таблицы критических значений - отношений при разных уровнях значимости нулевой гипотезы и различном числе степеней свободы. Табличное значение - критерия – это максимальная величина отношения дисперсий, которая может иметь место при случайном расхождении их для данного уровня вероятности наличия нулевой гипотезы. Вычисленное значение - отношения признается достоверным (отличным от единицы), если оно больше табличного. В этом случае нулевая гипотеза об отсутствии связи признаков отклоняется и делается вывод о существенности этой связи:

Если же величина окажется меньше табличной, то вероятность нулевой гипотезы выше заданного уровня (например, 0, 5 или 0, 1 или 0, 01) и она не может быть отклонена без риска сделать неправильный вывод о наличии связи. В этом случае уравнение регрессии считается статистически незначимым:

Величина -критерия связана с коэффициентом детерминации (или ). Факторную (регрессионную, объясненную) сумму квадратов можно представить как

а остаточную сумму квадратов – как

Тогда значение -критерия в соответствии (2.13) можно выразить так:

 

123Следующая ⇒

Поделиться:

Популярное:

1. V2: Линейная модель множественной регрессии
2. V6: Нелинейные модели регрессии
3. VII. Проанализируйте специфику библейского языка на основе представленных параллельных текстов.
4. Активность избирателей; неравенство доходов; показатель качества демократии по Р. Далю
5. Алгоритм построения групповой оценки на основе индивидуальных оценок экспертов
6. Анализ и оценка ликвидности и платежеспособности ООО «Торговый дом «Электрокабель»
7. Анализ и оценка системы управления персоналом в ПИК «СибЭкоДом»
8. Анализ и оценка финансовых результатов.
9. Анализ и оценка эффективности использования трудовых ресурсов.
10. Анализ Качества импульсных и цифровых САР.
11. Анализ качества оказываемых услуг
12. Анализ поведения потребителя на основе порядкового