Система аксиом Цермело–Френкеля и некоторые следствия из неё
Прежде — о первоначальных (неопределяемых) понятиях. Первым нелогическим конкретным неопределяемым предикатным символом является двухместный предикатный символ отношения принадлежности " 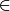 ", так что атомарные формулы имеют вид "
", так что атомарные формулы имеют вид "  " (читается: "
" (читается: "  принадлежит
принадлежит 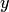 " ), "
" ), "  есть член (элемент)
есть член (элемент) 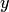 ", "
", "  содержится в
содержится в 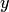 ", "
", " 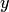 содержит
содержит  в качестве члена (элемента)". Вместо "
в качестве члена (элемента)". Вместо " 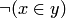 " условимся писать "
" условимся писать " 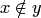 ". Вторым предикатным символом является двухместный предикатный символ отношения равенства " =", так что второй вид атомарных формул такой: "
". Вторым предикатным символом является двухместный предикатный символ отношения равенства " =", так что второй вид атомарных формул такой: " 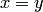 ". Первая аксиома характеризует отношение равенства.
". Первая аксиома характеризует отношение равенства.
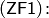 Аксиома объемности или аксиома экстенсиональности
Аксиома объемности или аксиома экстенсиональности
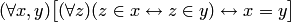
утверждает, что множества совпадают в том и только в том случае, если они состоят из одних и тех же элементов. Множества  и
и 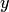 называются различными, если существует такой
называются различными, если существует такой  , что
, что 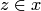 и
и 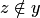 , или же существует
, или же существует  , что
, что  и
и 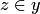 . Запись:
. Запись:  .
.
С помощью следующих определений вводится отношение включения:
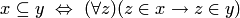
(запись " 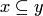 " читается: "
" читается: "  включается в
включается в 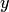 " или "
" или " 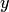 включает
включает  " ) и отношение строгого включения:
" ) и отношение строгого включения:
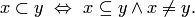
Между отношениями 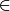 и
и 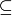 имеется весьма глубокое различие, которое необходимо понимать. Первое в нашем изложении является первоначальным, а второе вводится по определению. Но самое главное, что каждое множество включает себя само и свои подмножества, но, вообще говоря, не содержит (в качестве элементов) ни себя, ни своих подмножеств.
имеется весьма глубокое различие, которое необходимо понимать. Первое в нашем изложении является первоначальным, а второе вводится по определению. Но самое главное, что каждое множество включает себя само и свои подмножества, но, вообще говоря, не содержит (в качестве элементов) ни себя, ни своих подмножеств.
 Аксиома пустого множества:
Аксиома пустого множества:
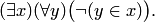
В этой аксиоме утверждается существование множества, не имеющего ни одного элемента. Такое множество называется пустым (или нулевым) и обозначается 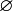 .
.
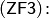 Аксиома неупорядоченных пар:
Аксиома неупорядоченных пар:
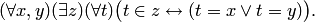
Множество  , существование которого для
, существование которого для 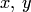 утверждается этой аксиомой, будем обозначать
утверждается этой аксиомой, будем обозначать 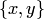 . Кроме того, через
. Кроме того, через 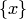 будем обозначать
будем обозначать  . Множество
. Множество 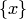 называется единичным, или одноэлементным.
называется единичным, или одноэлементным.
С помощью понятия неупорядоченной пары можно ввести понятие упорядоченной пары (это сделал К. Куратовский в 1921 г.). Двухэлементное множество  называется упорядоченной парой, составленной из
называется упорядоченной парой, составленной из 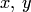 , и обозначается
, и обозначается 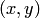 . Докажем следующее важнейшее свойство упорядоченной пары: если
. Докажем следующее важнейшее свойство упорядоченной пары: если  , то
, то  и
и  . В самом деле, рассмотрим следующие два случая:
. В самом деле, рассмотрим следующие два случая: 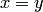 и
и  . При
. При 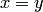 каждый элемент множества
каждый элемент множества  , то есть
, то есть 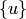 и
и  совпадает с
совпадает с 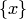 , откуда следует, что
, откуда следует, что  . При
. При  множество
множество 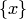 является элементом множества
является элементом множества 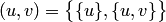 , т.е. одним из множеств
, т.е. одним из множеств 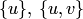 . Случай
. Случай 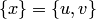 исключается, так как это равенство влечет
исключается, так как это равенство влечет  , откуда
, откуда 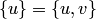 и
и 
 , что противоречит допущению
, что противоречит допущению  . Следовательно,
. Следовательно,  , а значит,
, а значит,  . Кроме того, в этом случае второй элемент
. Кроме того, в этом случае второй элемент 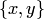 множества
множества 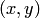 должен совпадать с
должен совпадать с 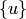 или с
или с  . Совпадение
. Совпадение  влечет
влечет  , что противоречит допущению
, что противоречит допущению  . Поэтому
. Поэтому 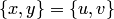 , откуда
, откуда 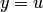 или
или  . Поскольку
. Поскольку  и
и  , то случай
, то случай 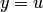 невозможен. Остается
невозможен. Остается  .
.
После того как определено понятие упорядоченной пары, представляется возможным определить понятие функции. Функция (или отображение) — это такое множество 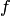 упорядоченных пар
упорядоченных пар 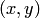 , что если
, что если 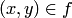 и
и 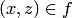 , то
, то 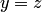 . При этом множество всех таких
. При этом множество всех таких  , что
, что 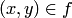 (для некоторого
(для некоторого 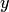 ), называется областью определения
), называется областью определения 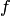 . Множество всех таких
. Множество всех таких 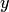 , что
, что 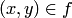 (хотя бы для одного
(хотя бы для одного  ), называется областью значений
), называется областью значений 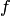 .
.
 Аксиома суммы, или некоторого объединения (введена Г. Кантором в 1899 г. и Цермело в 1908 г.):
Аксиома суммы, или некоторого объединения (введена Г. Кантором в 1899 г. и Цермело в 1908 г.):
утверждает, что существует множество 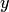 , являющееся объединением всех множеств из
, являющееся объединением всех множеств из  . Оно обозначается
. Оно обозначается  . В частности, если мы имеем два множества
. В частности, если мы имеем два множества 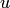 и
и  , то на основании аксиомы
, то на основании аксиомы 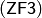 образуем двухэлементное множество
образуем двухэлементное множество 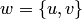 , а по аксиоме
, а по аксиоме 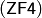 получаем существование такого множества
получаем существование такого множества 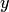 , что
, что 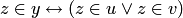 . Такое множество
. Такое множество  называется объединением множеств
называется объединением множеств 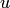 и
и  и обозначается
и обозначается 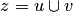 .
.
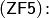 Аксиома множества подмножеств, или аксиома степени (сформулирована Цермело в 1908 г.):
Аксиома множества подмножеств, или аксиома степени (сформулирована Цермело в 1908 г.):
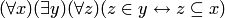
утверждает, что для каждого  существует множество
существует множество 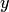 всех подмножеств этого
всех подмножеств этого  . Оно обозначается
. Оно обозначается  и называется множеством всех подмножеств
и называется множеством всех подмножеств  , или множеством-степенью
, или множеством-степенью  .
.
 Аксиома подстановки (сформулирована А. Френкелем в 1922 г. и Т. Скулемом в 1923 г.):
Аксиома подстановки (сформулирована А. Френкелем в 1922 г. и Т. Скулемом в 1923 г.):

Пусть 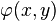 — такая формула, что при любом
— такая формула, что при любом  из множества
из множества 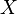 существует, и притом единственный, объект
существует, и притом единственный, объект  такой, что выражение
такой, что выражение  истинно. Тогда объекты
истинно. Тогда объекты  , для каждого из которых существует
, для каждого из которых существует 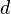 из
из 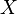 такой, что
такой, что  истинно, образуют множество. Схема подстановки содержит счётное количество аксиом, так как каждая подходящая формула
истинно, образуют множество. Схема подстановки содержит счётное количество аксиом, так как каждая подходящая формула 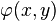 порождает аксиому.
порождает аксиому.
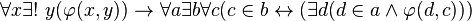
Таким образом, эта аксиома есть схема аксиом. Она утверждает, что образ при произвольном взаимно-однозначном отображении произвольного множества есть множество. В самом деле, условие данной аксиомы фактически означает, что формула  определяет
определяет 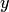 однозначно как функцию от
однозначно как функцию от  , то есть
, то есть 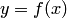 . Тогда заключение утверждает, что совокупность всех таких элементов
. Тогда заключение утверждает, что совокупность всех таких элементов  , которые являются образами при отображении
, которые являются образами при отображении 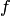 элементов из множества
элементов из множества 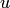 (то есть
(то есть 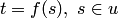 ), образует множество
), образует множество  .
.
Эта аксиома является исключительно сильной. Из нее может быть выведено следующее более слабое утверждение.
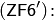 Аксиома выделения:
Аксиома выделения:
где  — формула, содержащая свободную переменную
— формула, содержащая свободную переменную  и не содержащая свободной переменной
и не содержащая свободной переменной  .
.
Аксиома утверждает, что для каждого  существует некоторое множество
существует некоторое множество  , состоящее из всех тех
, состоящее из всех тех  из
из  , которые обладают свойством
, которые обладают свойством  . В связи с аксиомой выделения имеет смысл еще раз вернуться к парадоксу Рассела и проанализировать причину появления этого парадокса и ему подобных в " наивной" теории множеств. Это в значительной мере обусловлено тем, что в " наивной" теории множеств мы наивно полагаем будто каждое свойство определяет некоторое множество. Парадокс Рассела как раз и демонстрирует нам, что это не так. Рассматривая свойство "
. В связи с аксиомой выделения имеет смысл еще раз вернуться к парадоксу Рассела и проанализировать причину появления этого парадокса и ему подобных в " наивной" теории множеств. Это в значительной мере обусловлено тем, что в " наивной" теории множеств мы наивно полагаем будто каждое свойство определяет некоторое множество. Парадокс Рассела как раз и демонстрирует нам, что это не так. Рассматривая свойство "  " и множество
" и множество 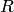 объектов, обладающих им:
объектов, обладающих им: 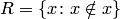 , приходим к следующему противоречию: по определению
, приходим к следующему противоречию: по определению 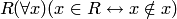 , тогда после подстановки
, тогда после подстановки 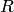 вместо
вместо  сразу получаем
сразу получаем  — противоречие. Таким образом, при построении формальной теории множеств надо стараться избегать таких свойств, которые могут привести к " абсурдным" множествам типа только что рассмотренного множества
— противоречие. Таким образом, при построении формальной теории множеств надо стараться избегать таких свойств, которые могут привести к " абсурдным" множествам типа только что рассмотренного множества 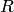 Рассела. Это и достигается с помощью аксиомы выделения: она допускает рассматривать не безграничные совокупности объектов, удовлетворяющие тому или иному свойству, а лишь те объекты, удовлетворяющие данному свойству, которые находятся внутри наперед заданного множества. Аксиома выделения является, пожалуй, самой характерной особенностью системы Цер-мело, отличая ее как от доаксиоматического подхода к теории множеств, так и от других аксиоматических систем.
Рассела. Это и достигается с помощью аксиомы выделения: она допускает рассматривать не безграничные совокупности объектов, удовлетворяющие тому или иному свойству, а лишь те объекты, удовлетворяющие данному свойству, которые находятся внутри наперед заданного множества. Аксиома выделения является, пожалуй, самой характерной особенностью системы Цер-мело, отличая ее как от доаксиоматического подхода к теории множеств, так и от других аксиоматических систем.
Аксиома выделения позволяет доказать следующие две теоремы, предоставляющие в наше распоряжение две важные теоретико-множественные конструкции.
Теорема о пересечении множеств. Для любых двух множеств  и
и 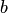 существует вполне определенное множество членов, содержащихся как в
существует вполне определенное множество членов, содержащихся как в  , так и в
, так и в 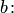

(Более общо, для каждого непустого множества 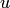 существует вполне определенное множество
существует вполне определенное множество  членов, содержащихся во всех членах из
членов, содержащихся во всех членах из 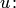
Множество  называется пересечением множеств
называется пересечением множеств  и
и 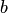 и обозначается
и обозначается 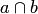 . Множество v называется пересечением множеств из
. Множество v называется пересечением множеств из 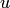 и обозначается
и обозначается 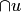 .)
.)
Доказательство. Множество 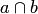 может быть определено как подмножество множества
может быть определено как подмножество множества  , соответствующее условию
, соответствующее условию  в аксиоме
в аксиоме 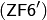 . Что касается
. Что касается 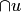 , то по аксиоме
, то по аксиоме 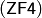 существует множество
существует множество 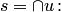 каждый элемент из
каждый элемент из  содержится по крайней мере в одном члене из
содержится по крайней мере в одном члене из 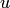 . Возьмем в качестве
. Возьмем в качестве  условие: "
условие: "  содержится в каждом члене из
содержится в каждом члене из 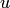 ". Тогда по аксиоме
". Тогда по аксиоме 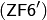 существует подмножество
существует подмножество  множества
множества  , членами которого будут в точности те, что содержатся во всех членах
, членами которого будут в точности те, что содержатся во всех членах 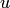 , то есть
, то есть 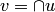 . (Если ни одного
. (Если ни одного  , общего для всех членов
, общего для всех членов 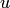 , нет, то имеем
, нет, то имеем  ).
).
Множество  называется дизъюнктным (или расчлененным), если никакие два члена из
называется дизъюнктным (или расчлененным), если никакие два члена из  не пересекаются, т. е.
не пересекаются, т. е.
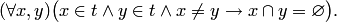
Теорема о декартовом произведении множеств. Для каждого дизъюнктного множества  существует вполне определенное множество, членами которого являются в точности все те множества, которые содержат по единственному члену из каждого члена
существует вполне определенное множество, членами которого являются в точности все те множества, которые содержат по единственному члену из каждого члена  .
.
(Это множество называется декартовым или прямым произведением членов  и обозначается
и обозначается 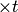 ; пишут также
; пишут также  , где
, где 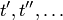 — суть члены
— суть члены  .)
.)
Если  содержит член
содержит член 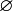 , то
, то 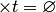 .
.
Доказательство. Поскольку члены искомого множества суть некоторые подмножества  , мы будем исходить из множества-степени множества
, мы будем исходить из множества-степени множества  , т.е. из
, т.е. из 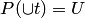 , существующего согласно аксиомам
, существующего согласно аксиомам 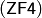 и
и  . В качестве условия
. В качестве условия  выберем следующее: "
выберем следующее: "  и для каждого
и для каждого  пересечение
пересечение 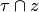 есть одноэлементное множество". Тогда по аксиоме
есть одноэлементное множество". Тогда по аксиоме 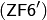 существует множество
существует множество 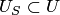 , членами которого являются те подмножества множества
, членами которого являются те подмножества множества  , которые содержат в точности по одному члену из каждого члена
, которые содержат в точности по одному члену из каждого члена  .
.
Утверждение теоремы в случае  очевидно: поскольку
очевидно: поскольку  не содержит членов, никакое множество не имеет с
не содержит членов, никакое множество не имеет с  общих членов. Теорема доказана.
общих членов. Теорема доказана.
Таким образом, из трех операций над множествами, известными из " наивной" теории множеств, — объединения, пересечения и прямого произведения — выполнимость первой в системе 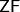 постулирована аксиомой
постулирована аксиомой 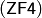 , а выполнимость двух других доказана при помощи аксиом
, а выполнимость двух других доказана при помощи аксиом 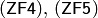 и
и 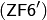 .
.
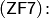 Аксиома бесконечности (введена Цермело в 1908 г.):
Аксиома бесконечности (введена Цермело в 1908 г.):
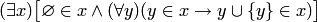
постулирует существование бесконечного множества. Ясно, что " первые" члены любого множества, удовлетворяющего этой аксиоме, суть следующие: 
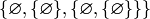 и т. д.
и т. д.
Если опустить эту аксиому, то в качестве модели для оставшейся системы аксиом можно взять совокупность всех конечных множеств, которые можно построить, отправляясь от пустого множества  . Ясно, что эта совокупность действительно будет моделью для всех остальных аксиом системы
. Ясно, что эта совокупность действительно будет моделью для всех остальных аксиом системы 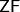 , так как ни одна из них не выводит за пределы класса конечных множеств, т.е., будучи применена к конечному множеству, утверждает существование такого множества, которое также должно быть конечным. Ясно, что никакое конечное множество не удовлетворяет аксиоме
, так как ни одна из них не выводит за пределы класса конечных множеств, т.е., будучи применена к конечному множеству, утверждает существование такого множества, которое также должно быть конечным. Ясно, что никакое конечное множество не удовлетворяет аксиоме 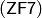 , а значит, на рассматриваемой модели из конечных множеств эта аксиома не выполняется. Это означает, что аксиома бесконечности
, а значит, на рассматриваемой модели из конечных множеств эта аксиома не выполняется. Это означает, что аксиома бесконечности 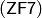 не зависит от остальных аксиом системы
не зависит от остальных аксиом системы 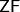 .
.
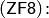 Аксиома фундирования, или аксиома регулярности (предложена Дж. фон Нейманом в 1925 г.):
Аксиома фундирования, или аксиома регулярности (предложена Дж. фон Нейманом в 1925 г.):
утверждает, что всякое непустое множество  содержит такой элемент
содержит такой элемент 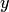 , что
, что  и
и 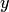 не имеют общих элементов. Из нее следует, что каждое непустое множество
не имеют общих элементов. Из нее следует, что каждое непустое множество  содержит элемент, минимальный по отношению
содержит элемент, минимальный по отношению 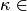 (но не
(но не 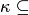 ). Следовательно, не может существовать такого множества
). Следовательно, не может существовать такого множества  , что
, что 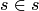 . В противном случае мы могли бы рассмотреть одноэлементное (и, значит, непустое) множество
. В противном случае мы могли бы рассмотреть одноэлементное (и, значит, непустое) множество 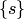 , для которого аксиома фундирования не выполнялась бы:
, для которого аксиома фундирования не выполнялась бы: 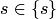 и множества
и множества  и
и 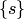 имеют общий элемент
имеют общий элемент  . Исключается существование таких множеств
. Исключается существование таких множеств 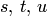 , для которых
, для которых 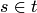 и
и  , или
, или  и т. д. Наконец, исключается существование бесконечных цепей, убывающих по отношению
и т. д. Наконец, исключается существование бесконечных цепей, убывающих по отношению 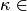 , т. е. таких множеств
, т. е. таких множеств  , которые имеют бесконечную убывающую последовательность своих членов:
, которые имеют бесконечную убывающую последовательность своих членов: 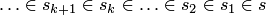 . Правда, при нарушении аксиомы фундирования такие убывающие цепи строятся лишь с помощью аксиомы выбора.
. Правда, при нарушении аксиомы фундирования такие убывающие цепи строятся лишь с помощью аксиомы выбора.
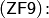 Аксиома выбора (введена Цермело в 1908 г.): если
Аксиома выбора (введена Цермело в 1908 г.): если  — дизъюнктное множество непустых множеств, то существует такое множество
— дизъюнктное множество непустых множеств, то существует такое множество 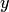 , которое из каждого множества из
, которое из каждого множества из  содержит точно по одному элементу (или: прямое произведение
содержит точно по одному элементу (или: прямое произведение 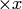 не пусто).
не пусто).
Иначе говоря, среди подмножеств множества  имеется по крайней мере одно, пересечение которого с каждым членом из
имеется по крайней мере одно, пересечение которого с каждым членом из  есть одноэлементное множество. Каждое такое подмножество и множества
есть одноэлементное множество. Каждое такое подмножество и множества  называется множеством представителей множества
называется множеством представителей множества  ; множество представителей, вообще говоря, не единственно.
; множество представителей, вообще говоря, не единственно.
Эту аксиому формулируют также в терминах понятия функции: для любого дизъюнктного множества  непустых множеств существует хотя бы одна такая функция
непустых множеств существует хотя бы одна такая функция 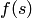 , областью определения которой служит
, областью определения которой служит  , что
, что 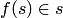 . Каждая такая функция определяет множество представителей множества
. Каждая такая функция определяет множество представителей множества  и называется функцией выбора.
и называется функцией выбора.
Аксиома выбора предоставляет наряду с аксиомой выделения еще один способ для получения подмножеств каких-либо множеств. Эта аксиома, пожалуй, одна из самых интересных и наиболее активно обсуждавшихся (несмотря на свое сравнительно позднее происхождение) аксиом математики. В этом отношении она уступает только евклидовой аксиоме о параллельных, имеющей более чем двухтысячелетнюю историю. Основные и важнейшие теоремы и методы теории множеств, алгебры, анализа, геометрии, топологии опираются на аксиому выбора. Поразительно большое количество теорем оказывается в точности эквивалентными аксиоме выбора. Фундаментальнейшая теорема Цермело о том, что всякое непустое множество можно вполне упорядочить, т.е. задать на нем такое линейное отношение порядка, что всякое непустое подмножество будет иметь наименьший элемент, — из числа важнейших эквивалентов аксиомы выбора. Хотя эта аксиома была осознана и явно сформулирована лишь в начале XX в., анализ показал, что применялась она в неявном виде задолго до этого времени. К аксиоме выбора математики пришли точно так же, как и к другим математическим принципам, — путем последующей проверки и логического анализа понятий, методов и доказательств, уже содержавшихся фактически в математике. Так, греческие математики догадались включить в число основных геометрических принципов аксиому о параллельных — утверждение, бытовавшее в математике задолго до Евклида. Гениальность этого достижения была полностью оценена лишь более двух тысячелетий спустя.
Итак, мы завершили перечисление аксиом теории множеств системы  Цермело–Френкеля. В настоящее время это наиболее употребительная в основаниях математики система аксиом, которой охватывается вся традиционная математика.
Цермело–Френкеля. В настоящее время это наиболее употребительная в основаниях математики система аксиом, которой охватывается вся традиционная математика.
Популярное:

