СТАТИЧЕСКИЙ РЕГРЕССИОННЫЙ АНАЛИЗ

1. Цель работы: Ознакомление с вопросами построения математического описания промышленных объектов в виде регрессионного уравнения по данным пассивного эксперимента.

Основы теории

Задачи эффективного прогноза и оптимального управления, задачи создания АСУ ТП требуют получения математического описания объектов и процессов, то есть их математических моделей. При этом в зависимости от специфики изучаемого технологического процесса его отдельные фазы (агрегаты) могут описываться статическими или динамическими уравнениями. Широкое распространение при построении моделей статических объектов получили так называемые " регрессионные модели" (1, 2, 3), когда объект описывается уравнением вида

(1)

где наблюдаемая в i-ом опыте выходная переменная;

- вектор " k" входных переменных в этом же опыте;

- значение случайной аддитивной помехи, распределенной по нормальному закону;

- вектор неизвестных коэффициентов;

- некоторая функция

Чаще всего исследователь не знает вида функции , которая может быть нелинейной как и по переменным , так и по параметрам . Обычно предполагают, что в области ограниченной экспериментом - гладкая функция, допускающая разложение в ряд Тейлора, и при построении модели ограничиваются конечным числом членов ряда. В этом случае регрессионное уравнение становится линейным относительно параметров , то есть имеет вид:

, (2)

где - вектор известных функций от входных переменных. Обычно степень аппроксимирующего полинома выбирается не выше второй.

При этом вектор 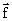в случае, например, двух входных переменных имеет вид

Легко видеть, что в случае (2) задача построения регрессионной модели сводится к задаче нахождения оценок

неизвестных коэффициентов .

Предположим, что реализован эксперимент, содержащий N опытов, в результате которого получена матрица значений входных переменных X и вектор значений выходной величины Y.

(3)

Для нахождения оценок уравнения (2) необходимо перейти от матрицы X к матрице

(4)

Располагая полученными матрицами Y и F, будем искать оценки в классе наилучших линейных несмещенных оценок, то есть потребуем, чтобы выполнялись три условия:

1. , которое означает линейность оценок относительно вектора Y.

2. , которое означает несмещенность оценок ;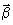

3. .

Последнее условие означает, что мы ищем наилучшую эффективную оценку, обладающую минимальной дисперсией по сравнению с другими возможными в этом классе оценками . Можно показать (4), что такая наилучшая линейная оценка определяется как

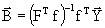(5)

Эта оценка кроме перечисленных выше обладает и другими замечательными свойствами. В частности, когда шум является нормально распределенной случайной величиной с нулевым математическим ожиданием и дисперсией , постоянной во всех опытах, оценка (5) совпадает с оценкой, найденной по методу максимального правдоподобия. Кроме того, эта оценка минимизирует дисперсию предсказания по регрессионной модели, то есть является одновременно МНК - оценкой (МНК - метод наименьших квадратов (4)).

Действительно, имея оценку , можно по регрессионной модели найти предсказанное значение выходной величины Y для заданного вектора

(6)

Нетрудно убедиться, что оценка 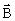обеспечивает минимальное значение суммы квадратов отклонений предсказанных значений от наблюдаемых в опыте ; то есть

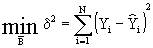(7)

Следовательно, оценка является одновременно МНК оценкой.

Располагая оценкой , можно кроме того найти несмещенную оценку дисперсии внешнего шума , которая определяется как

(8)

Однако отметим, что как оценка , найденная в соответствии с (5), так и оценка , будут обладать перечисленными выше оптимальными свойствами только при выполнении ряда условий, которые называются предпосылками регрессионного анализа (РА).

Сформулируем эти предпосылки.

1. Предполагается, что функция адекватно описывает объект. Это означает, что в модель включены все нужные входные переменные и правильно выбран вид модели, в частности, степень аппроксимирующего полинома.

2. Матрица является невырожденной матрицей, то есть

(9)

3. Входные переменные измеряются в опыте без ошибок.

4. Внешний шум подчиняется нормальному распределению с нулевым математическим ожиданием, дисперсией 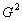, постоянной во всех опытах, и значения шума в соседних опытах некоррелированы, то есть

(10)

Очевидно, что найденные по формуле (5) оценки являются случайными величинами, так как они зависят от вектора Y, содержащего случайную помеху .

При выполнении предпосылок регрессионного анализа оценки подчиняются многомерному нормальному распределению вида

, (11)

где 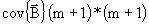- ковариационная матрица оценок , которая определяется как

(12)

и зависит от дисперсии внешнего шума , числа опытов N и матрицы , называемой информационной матрицей Фишера.

Если дисперсия внешнего шума неизвестная, то для оценивания ковариационной матрицы в выражение (12) вместо необходимо поставить ее оценку , рассчитанную в соответствии с (8).

Используя выражения (11) и (12), можно построить совместную доверительную область , внутри которой с заданной вероятностью а попадают неизвестные истинные значения коэффициентов .

С учетом (8) область определяется как

(13)

где - табличное значение критерия Фишера, найденное для уровня значимости и числа степеней свободы и

Можно видеть, что область является эллипсоидом в - мерном пространстве и ее объем может быть рассчитан по формуле

(14)

Очевидно, что чем больше объем доверительной области , тем менее точными являются найденные оценки .

В силу случайности оценок , предсказанное по формуле (6) значение выходной величины также будет случайным, то есть неизбежна ошибка прогноза

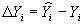, (15)

где - предсказанное, а - наблюдение в точке значения выходной величины.

 

Можно показать, что при выполнении предпосылок регрессионного анализа

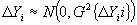(16)

то есть ошибка прогноза 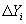является нормально распределенной случайной величиной с нулевым математическим ожиданием и дисперсией , которая определяется как

(17)

По аналогии с (13) точность прогноза можно характеризовать доверительным интервалом, внутри которого с заданной вероятностью a попадает наблюденное в точке значение выходной величины .

Можно показать, что доверительный интервал задается выражением

(18)

где табличное значение критерия Стьюдента, найденное для уровня значимости и числа степеней свободы .

Анализируя выражения (13) и (18), которые определяют точность найденных по экспериментальным данным оценок и точность прогноза регрессионной модели, можно сделать следующие выводы.

1. Точность регрессионного уравнения зависит от дисперсии внешнего шума и для увеличения точности необходимо стараться снизить уровень внешнего шума.

2. Ковариационная матрица оценок и дисперсия ошибки прогноза зависят от числа опытов N, по которым производилось вычисление оценок. Как видно из выражений (13) и (18), при стремлении N к бесконечности дисперсии оценок коэффициентов стремятся к нулю, а дисперсия ошибки прогноза стремиться к величине .

3. Точность регрессионной модели, в частности объем доверительного эллипсоида и ширина доверительного интервала (17) зависит от информационной матрицы

Если в процессе эксперимента возможно целенаправленное изменение входных переменных , то есть по ним возможен активный эксперимент, то естественно выбрать такую матрицу плана F, а следовательно, матрицу С, чтобы при заданном N обеспечить наибольшую точность регрессионной модели.
При выборе матрицы F используются различные критерии оптимальности плана эксперимента. Например, широкое распространение получили критерии: D-оптимальности, когда стараются максимизировать определитель матрицы С, а следовательно, минимизировать объем доверительной области (13); А - оптимальность, когда минимизируют след матрицы , то есть минимизируют сумму дисперсией оценок коэффициентов , т.п. (3).
Из теории планирования эксперимента известно, что в случае линейной относительно входных переменных регрессионной модели (то есть когда ), всем этим критериям удовлетворяет ортогональная матрица плана F, когда переменные варьируются на двух уровнях (3). Информационная матрица С в этом случае оказывается диагональной.
Однако отметим, что на реальных промышленных объектах проведение активного эксперимента часто оказывается невозможным, так как он связан с нарушением естественного хода технологического процесса и может приводить к браку и авариям. В этих условиях для построения математического описания объекта возможно использование лишь пассивного эксперимента, когда исследователь в ходе нормальной эксплуатации ТП регистрирует естественные изменения переменных. Если число опытов N в пассивном эксперименте задано (например, из экономических соображений с учетом их стоимости, но с учетом соотношения N> k), единственное, что экспериментатор может сделать для увеличения точности регрессионной модели, это выбрать оптимальным образом интервал съема данных .
Рассмотрим этот вопрос для случая линейной регрессионной модели

(19)

Предположим, что изменения входных переменных в ходе нормальной эксплуатации являются случайными, то есть можно рассматривать как случайные процессы .
Для простоты будем предполагать, что случайные процессы являются стационарными эргодическими гауссовскими процессами, то есть могут быть охарактеризованы своими математическими ожиданиями , дисперсиями , автокорреляционными функциями и взаимоковариационными функциями . Предположим, что задано число опытов N, выбран интервал съема данных (интервал дискретизации) и по этим дискретным отсчетам вычислены выборочные средние

(20)

где - значения j-й входной переменной в i-отсчете. Пусть произведено центрирование всех отсчетов, то есть вычислены значения
(21)
Тогда элементы информационной матрицы рассчитанной для центрированных отсчетов, определяются как

(22)

Из выражения (22) можно видеть, что эти элементы равны выборочным значениям нулевых ординат, соответствующих взаимно ковариационных функций .
Диагональные элементы матрицы есть выборочные дисперсии процессов или нулевые ординаты автокорреляционных функций , то есть . С учетом сказанного матрица С имеет вид
(23)

то есть является матрицей смешанных моментов процессов . Выше уже отмечалось, что для линейной модели (19) оптимальному плану эксперимента соответствует диагональная матрица С. Следовательно, при заданном числе опытов N в случае пассивного эксперимента необходимо стремиться выбрать интервал съема данных , чтобы получить наиболее близкую к диагональной информационную матрицу С с максимальным определителем. Очевидно, что для этого необходимо знать авто- и взаимоковариационные функции процессов . В частности, можно показать, что в случае , то есть когда при любых отсутствует взаимная ковариационная между переменными, оптимальный выбор должен производиться из условия

(24)
где - интервал корреляции (время затухания) процесса .
Выражение (24) требует, чтобы интервал между соседними отсчетами был больше, чем время затухания автокорреляционной функции самого " медленного" случайного процесса. Этот вывод может быть объяснен и качественно. Действительно, легко видеть, что при стремящемся к нулю, интервал наблюдения также стремится к нулю. При этом из-за сильной коррелированности отсчетов будет наблюдаться очень слабая их вариация относительно выборочного среднего, то есть отсчеты случайных процессов почти не будут отличаться друг от друга.
Очевидно, что в этом случае величины выборочной дисперсии стремятся к нулю, что ведет к вырождению информационной матрицы С и, следовательно, к резкому увеличению объема доверительной области .
Из сказанного ясно, что для увеличения значений выборочных дисперсий необходимо увеличить интервал съема данных. Однако не имеет смысла делать много больше времени , так как при этом продолжительность эксперимента существенно возрастает, а величины выборочных дисперсий практически не меняются.
В более общем случае, когда регрессионная модель нелинейна относительно переменных , оптимальный выбор может быть осуществлен путем численного решения задачи максимизации определителя информационной матрицы при заданных ковариационных функциях процессов .
Однако, в первом приближении и в этом случае можно рекомендовать выбор из условия (24). После того, как интервал съема данных выбран, осуществляется пассивный эксперимент, то есть в моменты времени , разделенные интервалом , измеряются значений входных переменных и выходной переменной . Полученные данные затем используются для нахождения оценок регрессионной модели по формуле (5) и оценки дисперсии внешнего шума по формуле (8).
Однако, необходимо подчеркнуть, что в случае пассивного эксперимента, даже оптимальный выбор вообще говоря, не гарантирует получения диагональной информационной матрицы, и для обеспечения необходимой точности регрессионной модели в этом случае необходимо увеличивать число экспериментальных точек N.
Кроме того, для снижения влияния ошибок округлений при расчете оценок в случае плохо обусловленной матрицы С обычно проводят стандартизацию переменных, когда элементы информационной матрицы вычисляются по формуле

(25)

Легко заметить, что диагональные элементы матрицы равны единице, а внедиагональные - выборочным коэффициентам корреляции процессов при .
Использование в формуле (5) матрицы вместо С приводит к вычислению стандартизованных оценок коэффициентов. Обратный переход от матрицы к необходимый для вычисления элементов ковариационной матрицы (12) и оценок в натуральном масштабе, осуществляется в соответствии с формулой

, (26)

где и - элементы матрицы и соответственно. Все указанные расчеты осуществляются, как правило, с помощью ЭВМ.
Для оценок работоспособности регрессионной модели, часто вычисляют множественный коэффициент корреляции
, (27)
где - выборочная дисперсия выходной переменной , рассчитанная относительно .
Коэффициент R характеризует тесноту связи между входными и выходной переменной, и при регрессионную модель можно считать достаточно точной.

Алгоритм расчета регрессионной модели