Многофакторный дисперсионный анализ.

Мы остановимся здесь на простейшем случае многофакторного дисперсионного анализа - двухфакторном анализе, то есть рассмотрим задачу оценки влияния двух одновременно действующих источников изменчивости А и В.
Пусть в примере с проверкой точности измерительных приборов все показания снимались несколькими операторами независимо друг от друга
В этом случае требуется выяснить обусловливается ли рассеивание полученных показаний и их средних значений в группах различием между приборами (фактор А) или различием между операторами, производившими замеры (фактор B)
Пусть по признаку А все наблюдения делятся на r групп , а по признаку В - на h групп , так что весь материал разбивается на rh групп; причем в каждой группе имеется l наблюдений (для простоты мы ограничиваемся случаем равночисленных наблюдений в группах, хотя и несущественно для теории). Таким образом, общее число наблюдений . Через мы обозначим отдельное наблюдение, попавшее в группу по признаку A и в группу по признаку В, индекс k означает номер замера в группе.
Пусть далее

(1) (2)

И, наконец,

(3)

Таблица с наблюдениями может быть представлена в следующем виде (таблица).
Результаты наблюдений за признаками А и В.

 

Основная идея дисперсионного анализа в данном случае, как и в разобранном выше случае однофакторного анализа, заключается в разложении суммы квадратов отклонений от общего среднего на компоненты, отвечающие предполагаемым факторам изменчивости. При этом тождеству (4) однофакторного анализа соответствует тождество

(4)

Или (5)

Выражения относят название суммы квадратов разностей между " строками" и между " столбцами". как и в однофакторном анализе называются соответственно " общей" и " остаточной" суммой квадратов.

Выполнение дисперсионного анализа и в этом случае заключается в проверке нуль - гипотезы об однородности общей совокупности значений ; то есть мы делаем предположение, что имеющаяся совокупность наблюдений является выборкой объема из генеральной совокупности , имеющей нормальное распределение с параметрами , где деленные на соответствующие степени свободы дадут несмещенные оценки дисперсии:

Каждая из этих оценок характеризует влияние одного из исследуемых факторов изменчивости на разброс показаний в общей совокупности. Так в нашем примере характеризует рассеивание за счет разницы в приборах (рассеивание средних по строкам), характеризует неоднородность, вносимую различием между операторами (рассеивание средних по столбцам) и, наконец, оценивает случайную погрешность измерений.
Для проверки степени значимости расхождений, обнаруженных в средних по строкам или по колонкам, вычисляются дисперсионные отношения:

Если какой-либо из критериев ( или ) превышает критическое значение , то нуль - гипотеза об однородности экспериментального материала должна быть отброшена, а влияние соответствующего фактора признано значимым.

2.2. Схема выполнения двухфакторного дисперсионного анализа.
Процедура выполнения двухфакторного дисперсионного анализа аналогична соответствующей схеме однофакторного анализа.
1. Исходный экспериментальный материал, классифицированный по признаку принадлежности к исследуемым факторам изменчивости, заносятся в табл.1. Там же вычисляются по формулам (1) и (2) средние по строкам и столбцам. Общее среднее, найденное по какой - либо из формул

Для контроля рекомендуется производить вычисление тем и другим способом. Результат заносится в таблицу 1 на пересечении столбца и строки .
2. Для упрощения дальнейших расчетов, как и в случае однофакторного анализа, производится преобразование переменных

3. Там же в табл.1 производятся некоторые подсчеты, которые понятны без пояснений. Заметим, только, что в клетку табл.1, разделенную диагональю, в ее нижнюю часть заносится сумма по j-элементам строки

;

а в верхнюю - сумма по i-элементам столбца
.
4. Суммы квадратов находятся с помощью удобных расчетных формул (7), (8), (9), (10)

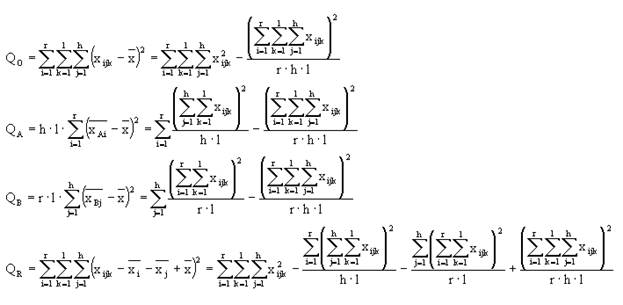
Для преобразованных переменных формулы (7)-(10) приобретают особенно простой вид, так как

.

5. Степени свободы для определения оценок дисперсии находятся по формулам

(11) (12) (13) (14)

Для контроля правильности определения степеней свободы можно использовать тождество:

(15)

6. Несмещенные оценки дисперсии 0находятся, как обычно, по формуле (19) (лабораторная работа №7).

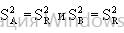7. Завершающий этап двухфакторного дисперсионного анализа состоит в проверке нуль - гипотезы , о равенстве оценок с помощью F-критерия, который проводится точно также, как и в случае однофакторного анализа.

Задание и порядок выполнения работы.

1. Ознакомиться с описанием лабораторной работы.

2. Разработать схему алгоритма дискретного анализа.

3. Составить текст программы и отладить ее.

4. Ввести исходные данные.

5. Получить распечатку результатов.

4. Контрольные вопросы

4.1. Что называется фактором изменчивости?
4.2. Какого типа практические задачи обычно решаются методом дисперсионного анализа?
4.3. Как математически формулируется задача многофакторного анализа?
4.4. Каковы основные предпосылки применения дисперсионного анализа?
4.5. В чем заключается основная идея метода?
4.6. Как формируются оценку дисперсии: общая, между группами и остаточная; разброс каких случайных величин они характеризуют?
4.7. Каким образом производится количественная оценка влияния фактора изменчивости?

 

 

ЛАБОРАТОРНАЯ РАБОТА N9

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Популярное:

1. Однофакторный дисперсионный анализ.