Однофакторный дисперсионный анализ.

В довольно общем виде задача однофакторного дисперсионного анализа ставится следующим образом: пусть мы наблюдаем m независимых

случайных величин , распределенных нормально с центрами и неизвестной но одинаковой для всех дисперсией .
Пусть над каждым переменным производится серия из n наблюдений (для простоты мы ограничимся случаем равночисленных наблюдений, хотя это несущественно для теории). Данные i-ой серии пусть будут .
Опираясь на эти статистические данные, требуется проверить нуль - гипотезу (H ₀) о равенстве математических ожиданий .
Если проверяемая гипотеза верна, то сопоставление средних в каждой серии не должно дать значимого расхождение между ними, и обратно, если такое расхождение обнаружено, то нулевую гипотезу следует отбросить. Аналогичная задача для случая решалась в лабораторной работе N1 с применением критерия Стьюдента. Однако для сравнения произвольно большого числа средних используется процедура дисперсионного анализа, связанная с применением F-критерия Фишера.
Указанной математической постановке может отвечать, например,
следующая практическая задача. Пусть при совместном анализе точности группы измерительных приборов нас интересует вопрос о том, можно ли считать их систематические ошибки одинаковыми. Иначе говоря, мы хотим проверить влияние одного фактора - прибора на погрешность показания. При этом каждый i-ый прибор является одним из элементов единственного фактора (источника) изменчивости.
Пусть число приборов равно m и каждым из них проводится n замеров некоторой (одной и той же) физической величины x.
Каждая серия из n измерений представляет собой выборку объема n из генеральной совокупности показаний отдельного прибора .
Всего мы располагаем измерениями, которые обозначим через 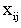, где i - номер прибора, j - номер произведенного на нем измерения. .
Таблица результатов измерений будет иметь следующий вид:

Среднее арифметическое из n показаний i-го прибора мы обозначили выше :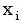

(1)

Если систематические ошибки приборов не одинаковы, то, очевидно, мы должны ожидать повышенного рассеивания выборочных средних

Обозначим через общую среднюю арифметическую всех измерений так, что

(2)
Совокупность наблюдаемых значений образуют выборку объемом из генеральной совокупности x, имеющей также нормальное распределение с центром и дисперсией , причем очевидно, что вычисленное с помощью (2) значение является оценкой математического ожидания 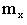по данным выборки.

Сущность дисперсионного анализа заключается в разложении дисперсии полученной частичной совокупности на составляющие, по рождаемые независимыми факторами. Каждая из этих составляющих дает оценку дисперсии в генеральной совокупности.

Практически мы рассматриваем три выборки из генеральной совокупности и по каждой ищем оценку для одной и той же дисперсии.

Для выполнения однофакторного дисперсионного анализа надо сумму квадратов отклонений значений от общего среднего разложить на составные части, одна из которых соответствует источнику изменчивости, другая - влиянию случайных причин.

Нетрудно установить тождество

(3)

Или

(4)

Здесь сумма

(5)

представляет сумму квадратов отклонений всех зарегистрированных значений от их общего среднего и называется " общей" или " полной" суммой квадратов

(6)

представляет собой взвешенную (с учетом числа замеров в каждой серии) сумму квадратов отклонений средних по группам (сериям) , от общего среднего и называется суммой квадратов " между группами" или " рассеиванием между элементами" фактора А, то есть за счет исследуемого источника изменчивости, который мы обозначили индексом А..

Сумма

(7)

является суммой квадратов отклонений наблюденных значений от средних соответствующей группы (серии) и называется суммой квадратов " внутри групп" или " серий". В силу тождества (4) в практических расчетах обычно вычисляется непосредственно только общая сумма и сумма квадратов между группами , сумма же квадратов внутри групп получается вычитанием из :

(8)

и поэтому называется " остаточной суммой квадратов".

Суммы квадратов деленные на соответствующие числа степеней свободы несут три несмещенные оценки дисперсии в общей совокупности :

(9), (10), (11)

Первая из этих оценок называется общей оценкой дисперсии, вторая - оценка дисперсии между группами и третья - остаточной оценкой дисперсии или оценкой дисперсии внутри групп.

Число степеней свободы проверяется путем сложения тем же способом, что и сумма квадратов (4), а именно:

(12)

Выполнение дисперсионного анализа заключается в сравнении оценки дисперсии, вызванной изучаемым фактором изменчивости А, и

остаточной оценкой дисперсии , имеющей место уже после того, как влияние фактора А было устранено, то есть обусловленной исключительно случайными погрешностями измерений.

Если нуль - гипотеза ( ) о равенстве центров

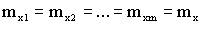
(в нашем случае систематические ошибки приборов одинаковы) верны, то, очевидно, оценки дисперсии должны различаться между собой лишь случайно. При этом критерий F Фишера

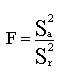
обычно применяемый для сравнения дисперсий, покажет с большой вероятностью лишь несущественные расхождения между указанными оценками.

Если же критерий F обнаружит значимое расхождение между , то это будет указывать на недопустимость нулевой гипотезы. В таком случае мы имеем основание признать материал неоднородным, то есть приходим к выводу, что источник изменчивости оказывает влияние на среднее значение случайных величин (у нас систематические погрешности приборов не одинаковы).

2.3. Cхема проведения однофакторного дисперсионного анализа.
1. Результаты испытаний , где i - номер серии (или элемента фактора изменчивости А), а j - номер замера в серии, заносятся в соответствующие графы таблицы.
На основе этих данных с помощью формул (1) и (2) вычисляются средние по строкам и общее среднее

2.Для удобства последующих вычислений совершается переход к новым переменным по формул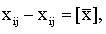е где - ближайшее к общему среднему целое значение.

Очевидно, при таком преобразовании переменных величины сумм квадратов не изменятся. Значения заносятся в соответствующие графы таблицы.

3. По значениям определяются промежуточные суммы, необходимые для дальнейшего анализа. Соответствующие подсчеты выполняются в таблице 1 и понятны без пояснений.

4. Производится вычисление сумм квадратов с помощью удобных расчетных формул:

(13), (14), (15)

Заметим, что при использовании преобразованных переменных соотношения (13) - (15) приобретают особенно простой вид, так как в этом случае

Остальные частные суммы необходимые для вычисления берутся из таблицы.

5. Определяются степени свободы по формулам:

(16), (17), (18)

6. Вычисляются несмещенные оценки дисперсии по известной формуле

(19)

7. Подсчитывается значение дисперсионного отношения - F-критерия Фишера

(20)

Напомним, что при формировании F-критерия в числителе становится большая из двух оценок дисперсии, то есть в нашем случае

(21)

8. По выбранной величине уровня значимости критерия F и соответствующим степеням свободы из таблицы находится критическое значение :

(22)

9. Вычисленное значение критерия F сравнивается с критической величиной и дается заключение о проводимой нуль - гипотезе . Если 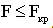, то есть, , то гипотеза принимается, если же , то есть , то гипотеза отвергается.

Все результаты пунктов 5-9 по мере их получения заносятся в соответствующие графы табл.1 отчета.

Задание и порядок выполнения работы

1. Ознакомиться с описанием лабораторной работы.

2. Разработать схему алгоритма дискретного анализа.

3. Составить текст программы и отладить ее.

4. Ввести исходные данные.

5. Получить распечатку результатов.

4. Контрольные вопросы

4.1. Что называется фактором изменчивости?
4.2. Какого типа практические задачи обычно решаются методом дисперсионного анализа?
4.3. Как математически формулируется задача однофакторного анализа?
4.4. Каковы основные предпосылки применения дисперсионного анализа?
4.5. В чем заключается основная идея метода?
4.6. Как формируются оценку дисперсии: общая, между группами и остаточная; разброс каких случайных величин они характеризуют?
4.7. Каким образом производится количественная оценка влияния фактора изменчивости?

 

ЛАБОРАТОРНАЯ РАБОТА N8

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Популярное:

1. Многофакторный дисперсионный анализ.