Силы действия и противодействия не уравновешиваются, так как они приложены к разным телам.
2.1.6 Аксиома 6 , аксиома отвердевания
Если деформируемое (не абсолютно твердое) тело находится в равновесии под действием некоторой системы сил, то равновесие его не нарушается и после того, как оно отвердеет (станет абсолютно твердым).
Принцип отвердевания приводит к выводу о том, что наложение дополнительных связей не изменяет равновесия тела и позволяет рассматривать деформируемые тела (тросы, цепи и пр.), находящиеся в равновесии, как абсолютно твердые тела и применять к ним методы статики.
Упражнения Консультации
6. На рисунке изображены пять эквивалентных систем сил. На основании каких аксиом или свойств сил доказанных на их основании, осуществлены преобразования исходной (первой) системы сил в каждую из последующих (первой во вторую, первой в третью и т.д.)

| 6.1Система сил (1.) преобразована в систему сил (2.) на основании аксиомы присоединения или отбрасывания систем взаимно уравновешивающихся сил  и и  . При присоединении или отбрасывании таких систем сил полученная система сил остается эквивалентной исходной системе сил и кинематическое состояние тела не изменяется.
6.2 Система сил (1.) преобразована в систему сил (3.) на основании свойства силы: силу можно переносить вдоль ее линии действия в пределах данного тела в любую точку, при этом кинематическое состояние тела или эквивалентность системы сил не изменяется.
6.3Система сил (1.) преобразована в систему сил (4.) путем переноса сил . При присоединении или отбрасывании таких систем сил полученная система сил остается эквивалентной исходной системе сил и кинематическое состояние тела не изменяется.
6.2 Система сил (1.) преобразована в систему сил (3.) на основании свойства силы: силу можно переносить вдоль ее линии действия в пределах данного тела в любую точку, при этом кинематическое состояние тела или эквивалентность системы сил не изменяется.
6.3Система сил (1.) преобразована в систему сил (4.) путем переноса сил  и и  вдоль их линии действия в точку С, а следовательно системы сил (1.) и (4.) эквивалентны.
6.4Система сил (1.) преобразована в систему сил (5.) путем перехода от системы сил (1.) к системе сил (4.) и сложения сил вдоль их линии действия в точку С, а следовательно системы сил (1.) и (4.) эквивалентны.
6.4Система сил (1.) преобразована в систему сил (5.) путем перехода от системы сил (1.) к системе сил (4.) и сложения сил  и и  в точке С на основании аксиомы о равнодействующей двух сил, приложенных в одной точке. в точке С на основании аксиомы о равнодействующей двух сил, приложенных в одной точке.
|
| 7. Вычислите равнодействующую двух сил Р1и Р2, если:
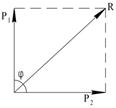
7 а) Р1 = Р2 = 2 Н, φ = 30º;
7б) Р1 = Р2 = 2 Н, φ = 90º.
| 7. Модуль равнодействующей сил Р1и Р2 определяется по формуле:
 7, а)
7, а)  ; ;
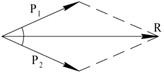 R = 3, 86 Н.
7, б) cos 90º = 0;
R = 3, 86 Н.
7, б) cos 90º = 0;
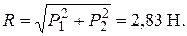
|
| 8. Сделайте рисунок и найдите равнодействующую для случаев:
8 а) Р1 = Р2 = 2 Н, φ = 120º;
8 б) Р1 = Р2 = 2 Н, φ = 0º;
8 в) Р1 = Р2 = 2 Н, φ = 180º.
| 8 а)  ; R =2H. ; R =2H.
 8 б) cos 0º = 1; R = Р1+Р2 = 4 Н.
8 б) cos 0º = 1; R = Р1+Р2 = 4 Н.
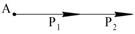 8 в) cos 180º = –1; R = Р2–Р1 = 2 – 2 = 0.
8 в) cos 180º = –1; R = Р2–Р1 = 2 – 2 = 0.
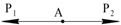 Примечание: если Р1 ≠ Р2 и Р1> Р2, то R направлена в ту же сторону, что и сила Р1.
Примечание: если Р1 ≠ Р2 и Р1> Р2, то R направлена в ту же сторону, что и сила Р1.
|
2.2 Рекомендуемая литература
Основная:
1). Яблонский А.А., Никифорова В.Л. Курс теоретической механики. М., 2002. с. 8 – 10.
2). Тарг С.М. Краткий курс теоретической механики. М., 2002. с. 11 – 15.
3). Цывильский В.Л. Теоретическая механика. М., 2001. с. 16 – 19.
4) Аркуша А.И. Руководство к решению задач по теоретической механике. М., 2000. с. 4 – 20.
Дополнительная:
5). Аркуша А.И. Техническая механика. М., 2002. с. 10 – 15.
6). Чернышов А.Д. Статика твердого тела. Красн-к., 1989. с. 13 – 20.
7). Эрдеди А.А. Теоретическая механика. Сопротивление материалов. М., 2001. с. 8 – 12.
8) Олофинская В.П. Техническая механика. М., 2003. с. 5 – 7.
Вопросы для самоконтроля
1. Привести примеры, иллюстрирующие аксиомы статики.
2. Объяснить положение: аксиомы статики установлены опытным путем.
3. Привести примеры применения аксиом статики в технике.
4. Сформулируйте аксиому о равновесии двух сил.
5. Назовите простейшую систему сил эквивалентную нулю.
6. В чем сущность аксиомы присоединения и исключения уравновешенной системы сил?
7. В чем физический смысл аксиомы отвердевания?
8. Сформулируйте правило параллелограмма сил.
9. Что выражает аксиома инерции?
10. Являются ли условия равновесия абсолютно твердого тела необходимыми и достаточными для равновесия деформируемых тел?
11. Приведите формулировку аксиомы равенства действия и противодействия.
12. В чем принципиальная ошибка выражения «действие и противодействие уравновешиваются»?
13. Как направлена равнодействующая R системы сил, если сумма проекций этих сил на ось OY равна нулю?
14. Как определяется проекция силы на ось?
15. Изложить алгоритм (порядок)определения модуля равнодействующей Fz, если заданы:
а) модуль и направление одной составляющей F, а также направления другой составляющей F2 и равнодействующей;
б) модули обеих составляющих и направление равнодействующей;
в) направления обеих составляющих и равнодействующей.
Тесты по теме
| 1.
| На рисунке изображены две силы, линии действия которых лежат в одной плоскости. Можно ли найти их равнодействующую по правилу параллелограмма?
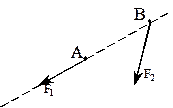 а) Можно.
б) Нельзя.
а) Можно.
б) Нельзя.
|
| 2.
| Вставьте пропущенное слово.
Проекция вектора на ось является … величиной.
а) векторной;
б) скалярной.
|
| 3.
| В каком из случаев, указанных на рисунках а), б) и в), перенос силы из точки А в точки В, С или Д не изменит механического состояния твердого тела?
 а) б) в)
а) б) в)
|
| 4.
| На рис. б) (см. пункт 3) изображены две силы, линии действия которых, лежат в одной плоскости. Можно ли найти их равнодействующую по правилу параллелограмма?
а) Можно;
б) Нельзя.
|
| 5.
| При каком значении угла между двух сил F1 и F2 их равнодействующая определяется по формуле FS = F1 + F2?
а) 0°;
б) 90° ;
в) 180°.
|
| 6.
| Чему равна проекция силы 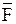 на ось y? на ось y?
 а) F× sina; б) -F× sina;
в) F× cosa; г) – F× cosa.
а) F× sina; б) -F× sina;
в) F× cosa; г) – F× cosa.
|
| 7.
| Если к абсолютно твердому телу приложить две силы, равные по модулю и направленные по одной прямой в противоположные стороны, то равновесие тела:
а) Нарушится; б) Не нарушится.
|
| 8.
| При каком значении угла между двух сил F1 и F2 их равнодействующая определяется по формуле FS = F1 - F2?
а) 0°;
б) 90°;
в) 180°.
|
| 9.
| Определить направление вектора силы  , если известно: Рх = 30Н,
Рy = 40Н.
а) cos , если известно: Рх = 30Н,
Рy = 40Н.
а) cos  = 3/4; cos = 3/4; cos  = 0.
б) cos = 0.
б) cos  = 0; cos = 0; cos  = 3/4.
в) cos = 3/4.
в) cos  = 3/5; cos = 3/5; cos  = 4/5.
г) cos = 4/5.
г) cos  = 3/4; cos = 3/4; cos  = 1/2. = 1/2.
|
| 10.
| Чему равен модуль равнодействующей двух сил?
 а)
а) 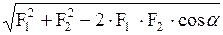 ;
б) ;
б) 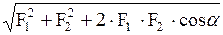 ;
в) ;
в)  ;
г) ;
г)  . .
|
| 11.
| Укажите правильное выражение для расчета проекции силы  на ось х, если модуль силы Р = 100 Н, на ось х, если модуль силы Р = 100 Н,  ; ; 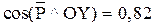 .
а) .
а) 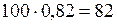 Н.
б) Н.
б)  Н.
в) Н.
в)  Н.
г) Н.
г) 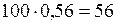 Н.
д) Правильного решения нет. Н.
д) Правильного решения нет.
|
| 12.
| Можно ли силу, приложенную к твердому телу, переносить вдоль линии действия без изменения действия силы на тело?
а) Можно всегда.
б) Нельзя ни при каких условиях.
в) Можно, если на тело не действуют другие силы.
|
| 13.
| Результат сложения векторов называется…
а) геометрической суммой.
б) алгебраической суммой.
|
| 14.
| Можно ли силу в 50 Н разложить на две силы, например, по 200 Н каждая?
а) Можно.
б) Нельзя.
|
| 15.
| Результат вычитания векторов называется…
а) геометрической разностью.
б) алгебраической разностью.
|
| 16.
| Чему равна проекция силы 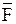 на ось х? на ось х?
 а) Fx = F× sina.
б) Fx = -F× sina.
в) Fx = -F× cosa.
г) Fx = F× cosa.
а) Fx = F× sina.
б) Fx = -F× sina.
в) Fx = -F× cosa.
г) Fx = F× cosa.
|
| 17.
| Является ли сила скользящим вектором?
а) Является.
б) Не является.
|
| 18.
| Две системы сил уравновешивают друг друга. Можно ли утверждать, что их равнодействующие равны по модулю и направлены по одной прямой?
а) Да.
б) Нет.
|
| 19.
| Определить модуль силы Р, если известны: Рх = 30 Н, Рy = 40 Н.
а) 70 Н;
б) 50 Н;
в) 80 Н;
г) 10 Н;
д) Нет правильного ответа.
|
| 20.
| Чему равна проекция силы  на ось y? на ось y?
 а) Рy = P× sin60°;
б) Рy = P× sin30°;
в) Рy = - P× cos30°;
г) Рy = -P× sin30°;
д) Нет правильного ответа.
а) Рy = P× sin60°;
б) Рy = P× sin30°;
в) Рy = - P× cos30°;
г) Рy = -P× sin30°;
д) Нет правильного ответа.
|
| 21.
| Зависят ли модуль и направление равнодействующей от порядка, в котором откладываются складываемые силы?
а) Зависят;
б) Не зависят.
|
| 22.
| При каком значении угла a между вектором силы и осью проекция силы на эту ось равна 0?
а) a =; б) a = 9°; в) a = 180°; г) a = 6°;
д) Нет правильного ответа.
|
| 23.
| Чему равна проекция силы 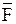 на ось х? на ось х?
 а) -F× sina;
б) F× sina;
в) -F× cosa;
г) F× cosa.
а) -F× sina;
б) F× sina;
в) -F× cosa;
г) F× cosa.
|
| 24.
| Определите модуль силы 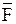 , если известны её проекции на оси x и y.
а) , если известны её проекции на оси x и y.
а)  ;
б) ;
б)  ;
в) ;
в)  ;
г) ;
г) 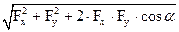 . .
|
| 25.
| Могут ли силы действия и противодействия взаимно уравновешиваться?
а) Не могут;
б) Могут.
|
| 26.
| Абсолютно твердое тело находится в равновесии под действием двух равных по величине сил F1 и F2. Нарушится ли равновесие тела, если эти силы будут перенесены, как показано на рисунке?
 а) Нарушится;
б) Не нарушится.
а) Нарушится;
б) Не нарушится.
|
| 27.
| Проекция вектора на ось равна:
а) произведению модуля вектора на косинус угла между вектором и положительным направлением оси координат;
б) произведению модуля вектора на синус угла между вектором и положительным направлением оси координат.
|
| 28.
| Почему силы действия и противодействия не могут взаимно уравновешиваться?
а) Эти силы не равны по модулю;
б) Они не направлены по одной прямой;
в) Они не направлены в противоположные стороны;
г) Они приложены к разным телам.
|
| 29.
| В каком случае две силы, действующие на твердое тело можно заменить их геометрической суммой?
а) В состоянии покоя;
б) В любом случае;
в) При движении;
г) В зависимости от дополнительных условий.
|
2.5 Задания для самостоятельной работы студентов
1). Изучить подраздел 2.1 данного методического указания, проработав предложенные упражнения.
2) Ответить на вопросы для самоконтроля и тесты по данному разделу.
3). Сделать дополнения в своем конспекте лекций, обращаясь также к рекомендуемой литературе.
4). Изучить и сделать краткий конспект следующего раздела «Д ействие над векторами » (4, с. 4-20), (7, с. 13, 14):
1.Сложение векторов. Правила параллелограмма, треугольника и многоугольника. Разложение вектора на два составляющих. Разность векторов.
3. Сложение и разложение векторов графоаналитическим способом.
4. Решить самостоятельно следующие номера задач (4, с. 14-16, 19): 6-2, 8-2, 9-2, 10-2, 13-3, 14-3.
Связи и их реакции
Понятия связей
Как уже отмечалось, в механике тела могут быть свободными и несвободными. Системы материальных тел (точек), положения и движения, которых подчинены некоторым геометрическим или кинематическим ограничениям, заданным наперед и не зависящим от начальных условий и заданных сил, называется несвободной. Эти ограничения, наложенные на систему и делающие ее несвободной, называются связями. Связи могут осуществляться с помощью различных физических средств: механических соединений, жидкостей, электромагнитных или других полей, упругих элементов.
Примерами несвободных тел являются груз, лежащий на столе, дверь, подвешенная на петлях, и т.п. Связями в этих случаях будут: для груза – плоскость стола, не дающая грузу перемещаться по вертикали вниз; для двери – петли, не дающие двери отойти от косяка. Связями также являются тросы для грузов, подшипники для валов, направляющие для ползунов и т.д.
Подвижно соединенные детали машин могут соприкасаться по плоской или цилиндрической поверхности, по линии или по точке. Наиболее распространен контакт между подвижными частями машин по плоскости. Так контактируют, например, ползун и направляющие пазы кривошипно-шатунного механизма, задняя бабка токарного станка и направляющие станины. По линии соприкасаются ролики с кольцами подшипника, опорные катки с цилиндрическим каркасом опрокидывателя вагонеток и т.д. Точечный контакт образуется в шарикоподшипниках между шариками и кольцами, между острыми опорными частями и плоскими деталями.
Популярное:

