Применение критерия Пирсона к проверке гипотезы о нормальном распределении генеральной совокупности

Пусть имеется наблюдений над случайной величиной . Пусть далее значения случайной величины распределены в интервалах с частотами и среднеинтервальными значениями .

Тогда можно записать эмпирическое распределение случайной величины Х в следующем виде:

(4.1)

где

(4.2)

Допустим, что анализ опытных данных привел к выбору некоторого теоретического распределения в качестве предполагаемого для данной случайной величины . Оценки параметров этого закона определим по выборке. С помощью указанного закона вычислим теоретические частоты для которых также

(4.3)

В качестве меры расхождения теоретического и эмпирического рядов частот можно взять величину

(4.4)

Сумма (4.4) распределена приближенно, как 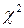- распределение (читается: «хи квадрат распределение») с плотностью распределения вероятностей

. (4.5)

и с числом степеней свободы 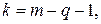где – число тех связей, которые были наложены на экспериментальный материал при оценке параметров распределения, необходимых для вычисления теоретических частот, а - число интервалов.

Применять 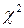- критерий нужно с известной осторожностью, так как он основан не на строгом законе, а на приближении, которым можно пользоваться, если условиться объединять крайние частоты ряда распределения так, чтобы частота объединенного разряда была не меньше 5.

При проверке гипотезы нормальности желательно, чтобы число наблюдений было не менее 50.

Схему применения критерия согласия 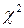рассмотрим на конкретном примере.

1.На основе опытных данных (см. столбцы 2 и 3 следующей ниже таблицы 4.1) предполагаем, что закон распределения случайной величины является нормальным и по известным формулам определяем выборочные оценки параметров его распределения: выборочную среднюю и выборочное среднее квадратическое отклонение .

Отметим, что поскольку групповая частота (см. табл. 4.1) в последней группе мала (меньше пяти) ее следует объединить с частотой предыдущей группы. В результате этого количество групп уменьшится с 10 до 9.

2.Введем в рассмотрение нормированную случайную величину

(4.6)

и вычислим теоретические частоты

(4.7)

где - объем выборки; - длина интервала; - нормированная функция плотности нормального распределения.

3. По формуле (4.4) вычисляем наблюдаемое значение критерия .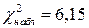

4.Определяем число степеней свободы .

5.По таблице распределения 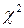находим критическое значение при уровне значимости 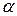=0, 05 и степенях свободы. Значение .

6.Делаем вывод: поскольку 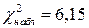меньше критического , то гипотеза о нормальном распределении частот верна.

7. Строим полигон частот и кривую распределения вероятностей (рис. 4.1).

 

Рис. 4.1. Полигон частот и кривая распределения вероятностей продолжительности периода полировки

 

Таблица 4.1. Распределение данных о продолжительности периода полировки ( )

Границы групп	Среднеинтер- вальные значения	Групповая эмпирическая частота	Нормированная случайная величина	Значения функции	Теоретическая частота		Накопленная эмпирическая частота	Накопленная теоретическая частота
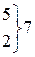
0, 83-1, 33 1, 33-1, 83 1, 83-2, 33 2, 33-2, 83 2, 83-3, 33 3, 33-3, 83 3, 83-4, 33 4, 33-4, 83 4, 83-5, 33 5, 33-5, 83	1, 08 1, 58 2, 08 2, 58 3, 08 3, 58 4, 08 4, 58 5, 08 5, 58		-2, 11 -1, 54 -0, 97 -0, 40 0, 17 0, 74 1, 32 1, 89 2, 46 3, 03	0, 0431 0, 1219 0, 2492 0, 3683 0, 3932 0, 3034 0, 1669 0, 0669 0, 0194 0, 0040		1, 12 0, 04 1, 84 0, 01 0, 22 0, 46 0, 13 0, 08 2, 25
Итого	-		-	-		6, 15	-	-	-

 

Таблица 4.2. Значения в зависимости от вероятности

и числа 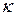степеней свободы 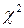- распределения.

Число степеней свободы	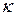Вероятность
0, 10	0, 05	0, 01
	2, 7 4, 6 6, 3 7, 8 9, 2 10, 6 12, 0 13, 4 14, 7 16, 0	3, 8 6, 0 7, 8 9, 5 11, 1 12, 6 14, 1 15, 5 16, 9 18, 3	6, 6 9, 2 11, 3 13, 3 15, 1 16, 8 18, 5 20, 1 21, 7 23, 2

 

Применение критерия Колмогорова к проверке гипотезы о нормальном распределении генеральной совокупности

Крупнейший советский математик А.Н. Колмогоров в 1933 году для оценки близости между эмпирическим и теоретическим распределениями предложил другой критерий, который основан на соотношении накопленных частот ( 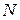) теоретического и эмпирического рядов распределений. Он ввел в рассмотрение случайную величину

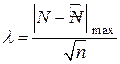(4.8)

и нашел функцию распределения этой величины

, (4.9)

которую назвали функцией Колмогорова.

Видный советский математик Н.В. Смирнов составил таблицы распределения случайной величины .

Таблица 4.3.

0, 30 0, 35 0, 40 0, 45 0, 50 0, 55 0, 60 0, 65 0, 70	1, 000 0, 9997 0, 0972 0, 9874 0, 9689 0, 9228 0, 8643 0, 7920 0, 7112	0, 75 0, 80 0, 85 0, 90 0, 95 1, 00 1, 10 1, 20 1, 30	0, 6272 0, 5441 0, 4653 0, 8927 0, 3275 0, 2700 0, 1777 0, 1122 0, 0681	1, 40 1, 50 1, 60 1, 70 1, 80 1, 90 2, 00 2, 10 2, 20	0, 0897 0, 0222 0, 0120 0, 0062 0, 0082 0, 0015 0, 0007 0, 0003 0, 0001

 

Если найденному значению соответствует очень малая вероятность , то расхождение между эмпирическим и теоретическим распределениями нельзя считать случайным. Если же величина значительна, то расхождение между частотами случайно, и эмпирическое распределение хорошо согласуется с теоретическим.

По данным таблицы 4.1 (см. столбцы 8, 9 и 10) имеем

(4.10)

По таблице вероятностей находим , следовательно, распределение данных о продолжительности периода полировки весьма близко к нормальному распределению.

Критерий В.И. Романовского

Видный советский математик В.И. Романовский предложил более удобную форму использования критерия 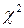, введя в рассмотрение величину где - число степеней свободы. Он доказал, что там, где эта величина меньше 3, расхождение между эмпирическим и теоретическим распределениями несущественно. Если же отношение Романовского больше 3, то расхождение между эмпирическим и теоретическим распределениями является неслучайным и теоретическое распределение не может служить моделью взятых эмпирических данных.

По найденным значениям и 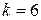определим величину

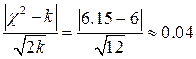(4.11)

Так как , то расхождение между эмпирическим и теоретическим распределениями данных о продолжительности периода полировки является несущественным.

 

4.4. Критерий Б.С. Ястремского

Критерий крупнейшего советского статистика Б.С. Ястремского выражается отношением

(4.12)

где - число групп, 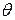- параметр, зависящий от числа групп.

При величина 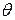=0, 6 и поэтому в этом случае отношение Ястремского имеет вид:

(4.13)

Критерий Ястремского имеет тот же смысл, что и критерий Романовского. По данному определим значение отношения (4.12):

(4.14

)

Так как , то гипотеза о нормальном распределении данных о продолжительности периода полировке противоречит результатам наблюдения.

Регрессионный анализ

Линейная корреляция

Если обе линии регрессии на и на - прямые, то корреляцию называют линейной.

Выборочное уравнение прямой линии регрессии на Х имеет вид

(5.1)

где - условная средняя; - выборочные средние признаков и ; - выборочные средние квадратические отклонения; 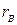- выборочный коэффициент корреляции, причем

Выборочное уравнение прямой регрессии Х на Y имеет вид

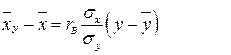(5.2)

Если данные наблюдений над признаками и заданы в виде корреляционной таблицы с равноотстоящими вариантами, то целесообразно перейти к условным вариантам.

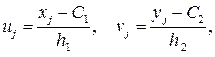
где 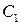- «ложный ноль» варианты (новое начало отсчета); в качестве ложного нуля выгодно принять варианту, которая расположена примерно в середине вариационного ряда (условимся принимать в качестве ложного ноля варианту, имеющую наибольшую частоту); - шаг, т.е. разность между двумя соседними вариантами ; - ложный нуль варианты Y; - шаг варианты .

В этом случае выборочный коэффициент корреляции

прилагаем слагаемое удобно вычислять, используя расчетную таблицу 5.3.

Величины 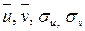могут быть найдены либо методом произведений (при большом числе данных), либо непосредственно по формулам

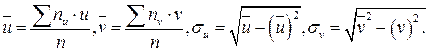
Зная эти величины, можно определить входящие в уравнения регрессии (5.1) и (5.2) величины по формулам:

Для оценки линейной корреляционной связи служит выборочный коэффициент корреляции 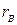; чем ближе к единице, тем связь сильнее; чем ближе к нулю, тем связь слабее.

Пример 5.1. Найти выборочное уравнение прямой линии регрессии на по данным, приведенным в корреляционной таблице 5.1.

Таблица 5.1

Х   Y
			-	-	-
	-			-	-
	-	-
	-	-
	-	-	-

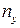
Решение. Составим корреляционную таблицу 5.2 в условных вариантах, выбрав в качестве ложных нулей (каждая из этих вариант расположена в середине соответствующего вариационного ряда).

Найдем 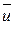и :

Найдем вспомогательные величины :

Найдем

Таблица 5.2

	-2	-1
-2			-	-	-
-1	-			-	-
	-	-
	-	-
	-	-	-

 

Найдем , для чего составим расчетную таблицу 5.3.

Суммируя числа последнего столбца таблицы 5.3, находим

Для контроля вычислений находим сумму чисел последней строки:

Таблица 5.3

	-2	-1
-2	-8 -8	-6 -12				-14
-1	-	-8 -8	-10			-8
	-	-
	-	-
	-	-	-
	-8	-20	-6
							Контроль

 

Совпадение сумм свидетельствует о правильности вычислений.

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Популярное:

1. I. Применение положений о поручительстве при рассмотрении дел в исковом порядке
2. Аминокислоты, их состав и химические свойства: взаимодействие с соляной кислотой, щелочами, друг с другом. Биологическая роль аминокислот и их применение.
3. Ароматические углеводороды. Бензол, структурная формула, строение, свойства. Применение бензола и его гомологов.
4. Б12/5. Применение метода остатка при оценке недвижимости, приносящей доход
5. База данных - это воплощенные на материальном носителе совокупности данных, подбор и расположение которых представляют результат творческого труда.
6. БАЛАНС: ПСИХОФИЗИЧЕСКОЕ ПРИМЕНЕНИЕ
7. Бесплодие при нормальном цикле
8. Биологические гипотезы происхождения языка
9. В условиях, связанных с применением физической силы, специальных средств, огнестрельного оружия
10. Виды диэлектриков. Применение твердых диэлектриков в энергетике.
11. Виды магнитных материалов. Применение магнитных материалов в энергетике. Свойства наиболее применяемых материалов. Электротехнические стали. Ферриты. Магнитодиэлектрики.
12. Всеобщая декларация прав человека. Принята резолюцией 217 А (III) Генеральной Ассамблеи ООН от 10 декабря 1948 года.