Решение транспортной задачи методом МОДИ

Решение транспортной задачи методом МОДИ позволяет легко принять правильное решение и за короткие сроки.

Используя данные из задания и результаты построения транспортной сети (Рис.1) формируется матрица исходных данных (табл.3).

 

Таблица 3

 

Исходные данные

Грузополучатели	Грузоотправители	Потребность в грузе, т
А1	А2	А3	А4
Б1
Б2
Б3
Б4
Б5
Наличие груза, т

 

Вторая стадия решения транспортной задачи заключается в построении опорного плана методом двойного предпочтения. Используя матрицу исходных данных (табл.3) и пример решения методом двойного предпочтения [1], проведя проверку, получаем опорный план (табл.4).

 

 

Таблица 4

 

Опорный план

Грузополучатели	Грузоотправители	Потребность в грузе, т
А1	А2	А3	А4
Б1	12(100)	11(100)
Б2		3(340)
Б3	10(100)
Б4			6(45)	2(135)
Б5			9(135)
Наличие груза, т

 

Пока не ясно является ли полученное в табл.4 распределение перевозок оптимальным. Для проверки оптимальности полученных данных используется специальную программу [2], которая позволяет найти оптимальное решение. Данные, полученные с помощи программы, отражаем в таблице оптимального плана (табл.5).

 

Таблица 5

 

Оптимальный план

Грузополучатели	Грузоотправители	Потребность в грузе, т
А1	А2	А3	А4
Б1
Б2
Б3
Б4
Б5
Наличие груза, т

 

Следующим шагом будет решение задачи маршрутизации перевозок. Данная задача решается методом совмещенных планов путем вписывания опорного плана (табл.4) в оптимальный план (табл.5), данное решение позволит выявить маятниковые и кольцевые схемы. После соединения планов получаем матрицу совмещенных планов (табл.6).

 

 

Таблица 6

 

Матрица совмещенных планов

 

Грузополучатели	Грузоотправители	Потребность в грузе, т
А1	А2	А3	А4
Б1	(200)
Б2		(340)
Б3		(100)
Б4			(45)	(135)
Б5			(135)
Наличие груза, т

 

Из оптимального плана (табл.5) видно, что имеются кольцевые схемы, вносим им в матрицу кольцевых схем (табл.7).

 

 

Таблица 7

 

Матрица кольцевых схем

Грузополучатели	Грузоотправители	Потребность в грузе, т
А1	А2	А3	А4
Б1	(100)
Б2
Б3		(100)
Б4
Б5
Наличие груза, т

Полученные из оптимального плана (табл.5) маятниковые и кольцевые схемы заносим в матрицу маятниковых и кольцевых схем (табл.8).

Таблица 8

 

Маятниковые и кольцевые схемы

Маршрут	Объем перевозок, т	Длина груженой ездки Lге, км	Длина маршрута Lм = 2Lге, км
А1Б1-Б1А1
А2Б2-Б2А2
А3Б4-Б4А3
А3Б5-Б5А3
А4Б4-Б4А4
А1Б1-А1Б3- Б3А2-Б1А2

По данной таблицы видно что получилось пять маятниковых маршрутов, и один кольцевой маршрут. Так же данные расчета показали что распределение груза было правильно потому что объем перевозки равен 995, что соответствует в задании.

Обоснование использования рационального типа подвижного состава в малой ненасыщенной системе

 

Производится расчет каждого выбранного ранее автомобиля, с учетом его загрузки и времени погрузки-разгрузки изменяя длину груженной ездки, ездки выбираются следующие: 1, 3, 5, 7, 9, 11, 13 км.

Урал 63685

lг=1 км.

Расчет времени оборота на маршруте t_об, ч.

(1)

где – длина маршрута, l_м= 2·l_г, км;

– среднетехническая скорость автомобиля, км/ч;

– время на погрузку, выгрузки, ч.

Расчет пропускной способности одного поста А^’, ед.

(2)

где t_погр- время погрузки, ч.

Округляем в меньшую сторону (по заданию малая ненасыщенная система).

Следовательно, А^'= 2ед.

 

Расчет времени возможной работы i-го автомобиля в системе T_Mi, ч.

, (3)

где – время в наряде, ч.

Расчет количества ездок i-го автомобиля в системе за смену, ед.

(4)

Расчет объема перевозок i-го автомобиля в системе, т.

, (5)

Расчет общего объема перевозок в малой ненасыщенной системе, т.

(6)

lг=3 км.

Расчет для l_г= 5 км, l_г= 7 км, l_г= 9 км, l_г= 11 км, а так же для автомобилей КрАЗ-65055-040 и МАЗ 55165-271 выполняются аналогично вышеприведенному примеру.

Результаты расчетов сводим в таблицу общую таблицу объемов перевозок (табл.9).

Таблица 9

 

Объемы перевозок

Длинна ездки с грузом, км	Объем перевозок в малой ненасыщенной системе при использовании, т
Урал 63685	КрАЗ-65055-040	КамАЗ 6520-26016-63

 

Для выявления автомашины с наибольшей выработкой строим график зависимости выработки автомашины, от изменения средней длинны груженой ездки (Рис.5).

 

КрАЗ-65055-040

Урал 63685

КамАЗ 6520-26016-63

 

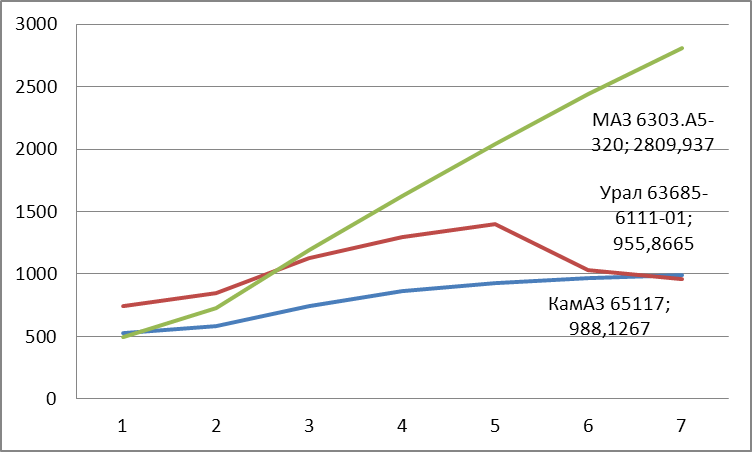
Рис.5. Изменение суммарной выработки автомобилей в малой ненасыщенной системе при изменении средней длинны груженой ездки.

 

Восстановив перпендикуляр для значения l_ге всех звеньев делаем вывод, что наилучшим к применению будет автомашина КамАЗ 6520-26016-63

(Рис.3), так как у него наибольшая выработка на этом участке

 

5 Расчет плановых показателей для автомобилей, перевозящих груз в малой ненасыщенной системе

 

Таблица 10

 

Исходные данные для расчета плановых показателей

⇐ Предыдущая123

Поделиться:

Популярное:

1. E) тело, размерами которого можно пренебречь в условиях данной задачи
2. GUDEL roboLoop уникальный робот с нелинейной транспортной системой
3. I. ОСНОВНЫЕ ЗАДАЧИ ВНЕШНЕЙ ПОЛИТИКИ
4. II. Основные цели и задачи Совета
5. II. Цели и задачи выпускной квалификационной работы
6. II. Цели и задачи настоящей Концепции
7. III. Задачи, определяемые возрастом воспитанников
8. III. Решение логических задач с помощью рассуждений
9. PR – отношения с общественностью. Цели, задачи, функции, методы
10. Адлер выделил три основные жизненные цели (задачи): работу, дружбу и любовь.
11. АЛГОРИТМ РЕШЕНИЯ СИТУАЦИОННОЙ ЗАДАЧИ №2
12. АЛГОРИТМ РЕШЕНИЯ СИТУАЦИОННОЙ ЗАДАЧИ №4