Случай регулярных внешних воздействий

Рассмотрим случай регулярных внешних воздействий для системы вида

(1)

где – неизвестное внешнее воздействие, которое можно представить в виде , где - вектор решения дифференциального уравнения

, , (2)

с неизвестным начальным условием .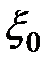

Например, постоянному воздействию 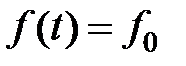соответствует уравнение 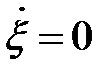, . Линейно нарастающему воздействию соответствуют уравнения , , , , и матрицы , . Гармоническому воздействию соответствуют уравнения , , , , и матрицы , .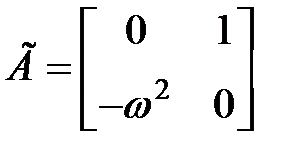

Уравнения (1), (2) запишем в виде одного уравнения:

(3)

где – - расширенный вектор состояния, – -матрица, – -вектор, – -вектор-строка.

Для оценки вектора состояния используется НУ:

. (4)

где – -вектор состояния. При выполнении условия наблюдаемости системы (3) может быть найден вектор параметров .

Полученную информацию о внешнем воздействии можно использовать для его компенсации в случае, когда в уравнении (1) , т.е. точки приложения управления и возмущения совпадают. В этом случае закон управления ищется в виде

. (5)

В этом случае исходную систему (1), замкнутую управлением (5), можно представить в виде

(6)

Учитывая, что , 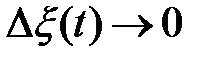при , то в силу устойчивости системы (6) решение будет стремиться к установившемуся значению , при котором .

Недостатком закона управления (4), (5) является зависимость установившейся ошибки от отклонения параметров реального ОУ и его математической модели (1), поскольку в этом случае точная компенсация по команде и возмущению не достигается.

Для устранения указанного недостатка строится общая модель для команды 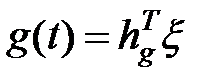и возмущения :

, . (7)

Вводится НУ отдельно для возмущения:

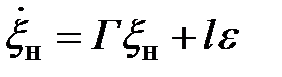, , (8)

где – -вектор параметров, подлежащих определению. Здесь на вход подается сигнал ошибки 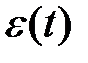, для которого с течением времени должно выполняться условие , достигающееся при компенсации действия команды и возмущения. Например, при постоянном входном сигнале значение может быть достигнуто, если матрица 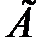имеет собственное значение равное нулю, что равносильно введению в систему интегрирующего звена. Поэтому использование НУ (8) расширяет возможности обеспечения астатизма системы.

Закон управления формируется в виде

, (9)

где – 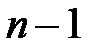-вектор динамического регулятора

, . (10)

Здесь матрица 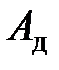обладает значительным запасом устойчивости, пара управляема. Например, матрицы можно принять в виде

, ,

где коэффициенты , соответствуют устойчивому желаемому полиному

Смысл системы (24) заключается в том, что с ее помощью формируется вектор с линейно независимыми координатами, зависящими от сигнала , т.е. появляется дополнительная информация для целей управления. Замкнутая система (1), (9), (8), (10) будет работоспособной, если она является устойчивой при отсутствии воздействий , . Для обеспечения устойчивости необходимо выбрать соответствующие значения , , , например, с помощью задания желаемых коэффициентов характеристического уравнения замкнутой системы, порядок которого равен . При этом число параметров, от которых зависят указанные коэффициенты, равно , т.е. можно произвольно задать параметров. Тогда при наличии воздействий , в установившемся режиме будет выполняться условие 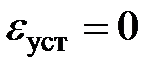для множества векторов , не обязательно совпадающих с вектором , при наличии отклонения параметров реального ОУ и его математической модели (1). Поэтому закон управления (9), (8), (10) называют грубым законом управления установившегося движения.

Недостатком данного закона управления также как и для систем с наблюдающим устройством является значительный начальный выброс координат вектора оценок, что приводит к броску управляющего сигнала и в некоторых случаях к увеличению перерегулирования выходной координаты. Поэтому на практике для исключения начального броска в режиме включения системы подключение устройств оценки осуществляется спустя некоторое время, за которое осуществляется необходимая оценка. В этот промежуток времени замкнутая система должна быть устойчивой за счет, например, обычного корректирующего устройства. После чего осуществляется переключение на регулятор с устройством оценки.

⇐ Предыдущая 1 2 345 Следующая ⇒