Оптимальная стратегия обновления оборудования

Предприятие в начале пятилетнего периода выделило млн. руб. для комплектования оборудования, стоимость единицы которого млн. руб. Единица оборудования за год приносит предприятию 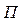млн. руб. прибыли. Необходимо разработать такую программу пополнения оборудования, чтобы суммарная прибыль от его внедрения в течение планового периода была максимальной.

Вариант 1.К=4 =2 П=0, 6

Вариант 2.К=4, 5 =1, 5 П=0, 5

Вариант 3.К=5 =2, 5 П=0, 8

Вариант 4.К=6 =2 П=0, 5

Вариант 5.К=3, 5 =1, 75 П=0, 8

Вариант 6.К=4 =2 П=0, 55

Вариант 7.К=5, 5 =2, 75 П=0, 8

Вариант 8.К=4, 5 =1, 5 П=0, 4

Вариант 9.К=5 =2, 5 П=0, 7

Вариант 10.К=6 =2 П=0, 6

 

Вопросы к зачёту по дисциплине «Методы оптимальных решений»

 

1. Примеры задач линейного программирования. Общая задача линейного программирования.
2. Графический метод решения задачи линейного программирования. Особые случаи решения задач линейного программирования.
3. Основы симплекс-метода линейного программирования. Особые случаи симплексного метода.
4. Метод искусственных переменных.
5. Двойственные задачи линейного программирования. Основные теоремы теории двойственности линейного программирования.
6. Объективно обусловленные оценки и их смысл.
7. Модели целочисленного линейного программирования.
8. Постановка задачи нелинейного программирования. Методы поиска экстремума целевой функции задачи нелинейного программирования.
9. Безусловный и условный экстремум. Теорема Лагранжа.
10. Оптимизационные задачи для выпуклых функций. Метод допустимых направлений.
11. Двойственность в нелинейном программировании.
12. Решение задач с линейными ограничениями.
13. Понятие многошагового процесса. Рекуррентные соотношения. Задача дискретного оптимального управления.
14. Основные идеи вычислительного метода динамического программирования.
15. Задачи динамического программирования, допускающие табличное задание рекуррентных соотношений.
16. Принцип оптимальности Беллмана. Примеры задач динамического программирования.
17. Основные понятия теории игр. Платёжная матрица игры. Верхняя и нижняя цена игры.
18. Игры с седловой точкой. Упрощение платёжной матрицы.
19. Доказательство основных теоремы теории игр: теоремы об активных стратегиях, теоремы Неймана о существовании решения.
20. Решение игр в смешанных стратегиях. Приведение матричной игры к задаче линейного программирования.
21. Игры с природой Корпоративные игры.
22. Понятие плоского графа. Ориентированные и неориентированные графы. Эйлеровы и гамильтоновы графы.
23. Понятия пути и цикла в графе. Дерево. Метод ветвей и границ. Задача о коммивояжере и ее решение методом ветвей и границ.
24. Понятие сети. Сетевые графики. Построение сетевых моделей. Расчёт и анализ сетевых моделей. Сети Петри.
25. Транспортная задача. Методы решения транспортных моделей.
26. Распределительная задача. Задача о назначениях.
27. Построение максимального потока в сети с заданными пропускными способностями. Задача о кратчайшем пути.
28. Компоненты и классификация моделей массового обслуживания.
29. Построение одноканальной модели с пуассоновским входным потоком с экспоненциальным распределением длительности обслуживания.
30. Построение одноканальной системы массового обслуживания с ожиданием.
31. Построение многоканальной модели с пуассоновским входным потоком и экспоненциальным распределением длительности обслуживания.
32. Построение многоканальной системы массового обслуживания с ожиданием.

 

Список литературы

Основная литература

 

1. Алесинская Т.В.Экономико-математические методы и модели. Учебное пособие по решению задач. Таганрог: изд-во ТРТУ, 2002, 153 с.

2. Вагнер Г. Основы исследования операций. Тома I-III. –М.: Мир, 1972-73гг.

3. Гнеденко Б.В., Коваленко И.Н.. Введение в теорию массового обслуживания. М., 1987.

4. Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике. – М.: ДИС, 1997

5. Ивченко Г.И., Каштанов В.А., Коваленко И.Н.. Теория массового обслуживания. М., 1982.

6. Карлин С. Математические методы в теории игр, программирование и экономика. – М.: Мир, 1964

7. Сидин Э.Ф. Экономико-математическое моделирование. Учебное пособие/ Чернигов. Изд-во Черниговского гос. ин-та экономики и управления, 1999г

8. Солопахо А.В. Математика в экономике. Учебно-практическое пособие/Тамбов. Изд-во Тамб.гос.техн. ун-та, 2001. ч. 1. 71с.

9. Тарасов В.Л. Экономико-математические методы и модели. Учебное пособие/ Нижний Новгород. Изд-во Нижегородского гос. ун-та, 2003. 64с.

10. Аллен Р. Математическая экономика- – М. Ил, 1963

11. Ашманов С.А. Введение в математическую экономику. – М.: Наука, 1984

12. Громенко В.В.Математическая экономика. Учебно-практическое пособие. М.: МЭСИ, 2004-100с.

13. Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике. – М.: ДИС, 1997

14. Колесников А. Н. Краткий курс математики для экономистов. – М.: ИНФРА-М, 1997

15. Сидин Э.Ф. Экономико-математическое моделирование. Учебное пособие/ Чернигов. Изд-во Черниговского гос. ин-та экономики и управления, 1999г

16. Солопахо А.В. Математика в экономике. Учебно-практическое пособие/Тамбов. Изд-во Тамб.гос.техн. ун-та, 2001. ч. 1. 71с.

17. Тарасов В.Л. Экономико-математические методы и модели. Учебное пособие/Нижний Новгород. Изд-во Нижегородского гос. ун-та, 2003. 64с.

 

Дополнительная литература

 

1. Исследование операций. Тома I, II. (под. ред. Дж. Моудера, С. Элмаграби) – М.: Мир, 1981
2. Бодров В.И., Лазарева Т.Я., Марте Ю.Ф.. Математические методы принятия решений. Учебное пособие. Тамбов. Изд-во ТГТУ 2004.
3. Кениг Д., Штойян Д.. Методы теории массового обслуживания: Пер. с нем. /Под. ред. Г.П.Климова. М., 1981.
4. Левин М. И., Макаров В.Л., Рубинов А. М. Математические модели экономического взаимодействия. – М.: Наука, 1993.
5. Гейл Д. Теория линейных экономических моделей. – М.: Ил, 1963
6. Данилов Н.Н., Иноземцева Л.П. Основы математической экономики: web- ориентированный учебник.- Электронное издание.- Кемерово: КемГУ, 1999.
7. Ланкастер К. Математическая экономика. – М.: Сов. радио, 1972

Экланд И. Элементы математической экономики. – М.:

 

⇐ Предыдущая3456789101112

Поделиться:

Популярное:

1. A.5.7. Панель тормозного оборудования
2. VIII. Стратегия выбора профессии
3. Анализ рынка и маркетинговая стратегия.
4. Анализ состояния оборудования, эффективности работы элементов технологической схемы
5. Б11.5 Цели, принципы и методы в оценки машин и оборудования. Области применения и ограничения методов оценки машин и оборудования
6. Безопасность технологических процессов и производственного оборудования
7. В.С. Ротенберг Мозг. Стратегия полушарий
8. Ведомость монтируемого электрооборудования
9. Возможные решения ситуации «Стратегия развития турфирмы «Парус»
10. Вопрос 20. Стратегия фирмы. Выбор стратегии.
11. Вопрос №4: Классификация оборудования для хранения материалов по назначению и конструктивным особенностям.
12. Вставка радиоканального оборудования