НЕЗАВИСИМЫЙ ИСТОЧНИК ПИТАНИЯ

НЕЗАВИСИМЫЙ ИСТОЧНИК ПИТАНИЯ

Виды соединений пассивных элементов

Последовательное соединение пассивных элементов

Участок цепи 4-5-6-1 представляет собой последовательное соединение резисторов. На рассматриваемом участке действует напряжение U, равное алгебраической сумме ЭДС левой части схемы. Это напряжение равно также сумме падений напряжения в правой части схемы:

Рис. 34

Вынеся I за скобку, получим

или

Отношение есть некоторое сопротивление, эквивалентное по своему действию всем трем сопротивлениям:

Это равенство позволяет на участке 4-5-6-1 три сопротивления заменить одним (эквивалентным) и получить более простую схему (рис. 35) при условии неизменности тока в цепи и сохранении того же баланса мощностей.

Рис. 35

Этот вывод можно распространить на любое число последовательно включенных пассивных элементов:

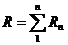т. е., общее сопротивление неразветвленной цепи равно сумме сопротивлений ее участков.

Законы Кирхгофа

Первый закон Кирхгофа

В цепях, состоящих из последовательно соединенных источника и приемника энергии, соотношения между током, ЭДС и сопротивлением всей цепи или, между напряжением и сопротивлением на каком-либо участке цепи определяется законом Ома.

На практике в цепях, токи, от какой-либо точки, идут по разным путям.
Точки, где сходятся несколько проводников, называются узлами, а участки цепи, соединяющие два соседних узла, ветвями.

В замкнутой электрической цепи ни в одной ее точке не могут скапливаться электрические заряды так, как это вызвало бы изменение потенциалов точек цепи. Поэтому электрические заряды притекающие к какому-либо узлу в единицу времени, равны зарядам, утекающим от этого узла за ту же единицу.
Разветвлённая цепь.
В узле А цепь разветвляется на четыре ветви, которые сходятся в узел В.

Обозначим токи в неразветвленной части цепи - I, а в ветвях соответственно

I1, I2, I3, I4.

У этих токов в такой цепи будет соотношение:

I = I1+I2+I3+I4;

Cумма токов, подходящих к узловой точке электрической цепи,
равна сумме токов, уходящих от этого узла.

При параллельном соединении резисторов ток проходит по четырем направлениям, что уменьшает общее сопротивление или увеличивает общую проводимость цепи, которая равна сумме проводимостей ветвей.

Обозначим силу тока в неразветвленной ветви буквой I.
Силу тока в отдельных ветвях соответственно I1, I2, I3 и I4.
Напряжение между точками A и B - U.
Общее сопротивление между этими точками — R.

По закону Ома напишем:

I = U/R; I1 = U/R1; I2 = U/R2; I3 = U/R3; I4 = U/R4;

Согласно первому закону Кирхгофа:

I = I1+I2+I3+I4; или U/R = U/R1+U/R2+U/R3+U/R4.

Сократив обе части полученного выражения на U получим:

1/R = 1/R1+1/R2+1/R3+1/R4, что и требовалось доказать.

Cоотношение для любого числа параллельно соединенных резисторов.
В случае, если в цепи содержится два параллельно соединенных резистора
R1 и R2, то можно написать равенство:

1/R =1/R1+1/R2;

Из этого равенства найдем сопротивление R, которым можно заменить два параллельно соединенных резистора:

Полученное выражение имеет большое практическое применение.
Благодаря этому закону производятся расчёты электрических цепей.

Второй закон Кирхгофа

В замкнутом контуре электрической цепи сумма всех эдс равна
сумме падения напряжения в сопротивлениях того же контура.

E1 + E2 + E3 +...+ En = I1R1 + I2R2 + I3R3 +...+ InRn.

При составлении уравнений выбирают направление обхода цепи и произвольно задаются направлениями токов.

Если в электрической цепи включены два источника энергии, эдс которых совпадают по направлению, т. е. согласно изо1, то эдс всей цепи равна сумме эдс этих источников,
т. е.
E = E1+E2.

Если же в цепь включено два источника, эдс которых имеют противоположные направления, т. е. включены встречно изо2, то общая эдс цепи равна разности эдс этих источников
Е = Е1—Е2.

		При последовательном включении в электрическую цепь нескольких источников энергии с различным направлением эдс общая эдс равна сумме эдс всех источников. Складывая эдс одного направления, берут со знаком плюс, а эдс противоположного направления - со знаком минус. В нашем случае, при встречном включении, положения щупов пришлись на противоположную полярность источника большего напряжения, поэтому на приборе отрицательный знак.

Благодаря этим законам производятся расчёты электрических цепей.
Существует несколько методов расчёта, один из них " Метод узловых напряжений"

7. Гармонические колебания. Основные понятия и определения

Электрические цепи могут находиться под воздействием постоянных или переменных напряжений и токов. Среди этих воздействий важнейшую роль играют гармонические колебания. Последние широко используются для передачи сигналов и электрической энергии, а также могут применяться в качестве простейшего испытательного сигнала. Исследование режима гармонических колебаний важно и с методической точки зрения, поскольку анализ электрических цепей при негармонических воздействиях можно свести к анализу цепи от совокупности гармонических воздействий. В этом смысле методику анализа и расчета цепей при гармонических воздействиях можно распространить и на цепи при периодических несинусоидальных, а также непериодических воздействиях (см. гл. 5, 9).

Гармоническое колебание i(t) (рис. 3.1) характеризуется следующими основными параметрами: амплитудой I_т; угловой частотой ω, начальной фазой φ _i. Амплитудой называют максимальное абсолютное значение тока i(t). Аналитически гармоническое колебание можно записать в виде

где — называется текущей фазой (или просто фазой) гармонического колебания, так как она растет линейно во времени с угловой скоростью Вместо формулы (3.1) гармоническое колебание можно выразить и в косинусоидальной форме:

Наименьший промежуток времени, по истечении которого значения функции i(t) повторяются, называется периодом Т. Между периодом Т и угловой частотой ω существует простая связь:

Величину, обратную периоду, называют циклической частотой: f = 1/Т. Из вышеизложенного следует, что ω = 2π f. Единицей ■ измерения частоты f является герц (Гц), угловой частоты ω — радиан в секунду (рад/с). Так как радиан — величина безразмерная, то [ω ] измеряется в 1/с или с^-1.

В радиотехнике и электросвязи используют гармонические сигналы от долей герц (инфранизкие частоты) до десятков и сотен гигагерц (сверхвысокие частоты).

Для питания различных электроэнергетических установок в России и ряде других стран принята промышленная частота f = 50 Гц. В качестве источников гармонических колебаний промышленной частоты используются электромашинные генераторы различного типа. Принцип работы простейшего электромашинного генератора иллюстрирует рис. 3.2. В состав генератора входят: статор, создающий магнитное поле с магнитной индукцией В, и ротор, вращающийся в этом магнитном поле с угловой частотой ω. При пересечении витками катушки ротора магнитного потока Ф в них согласно закону электромагнитной индукции наводится ЭДС

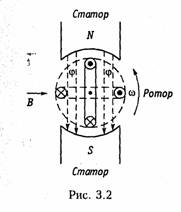
где ψ = wФ— потокосцепление катушки с магнитными потоками; w — число витков катушки. При постоянной скорости вращения ротора для получения ЭДС синусоидальной формы применяются полюса специальной формы. Частота на выходе генератора

где р_п — число пар полюсов ротора; v — частота вращения ротора, об/мин.

Электромашинные генераторы используются для получения гармонических напряжений и токов не выше 5...8 кГц. Для получения гармонических сигналов более высоких частот обычно используются ламповые и полупроводниковые генераторы (см. гл. 15).

Важными параметрами гармонических колебаний являются их действующее и среднее значения. Действующее значение гармонического тока

Действующие значения токов и напряжений называют еще их среднеквадратическими значениями.

Определим тепловую энергию, которая выделяется гармоническим колебанием i(t) за период Т в резистивном элементе с сопротивлением R:

Таким образом, действующее значение тока численно равно такому постоянному току, который за период Т на том же сопротивлении выделяет то же количество тепла, что и гармонический ток.

Среднее значение гармонического тока

Подставив значение i из (3.6) в (3.9), находим, что I_ср = 0. Этот результат вполне понятен, если учесть, что уравнение (3.9) определяет площадь, ограниченную кривой i(t) за период Т (см. рис. 3.1). Если значение тока определено за полпериода, то можно записать:

8. Метод контурных токов

Для расчета режима сложной электрической цепи можно ограничиться совместным решением лишь К = (В - У + 1) независимых уравнений, составленных на основании второго закона Кирхгофа методом контурных токов; здесь В, как и ранее, -число ветвей и У - число узлов, при этом первый закон Кирхгофа, конечно, всегда удовлетворяется.
Для иллюстрации применения метода контурных токов рассмотрим схему на рис. 1.21, а с шестью ветвями и четырьмя узлами. Прежде чем составлять уравнения по второму закону Кирхгофа, надо выбрать взаимно независимые контуры.
При выборе независимых контуров можно применять то же правило, что и при записи уравнений по второму закону Кирхгофа. Например, для схемы рис. 1.21, а ветви с токами I4, I5 и I6, соединяющие узлы 1, 2, 3, 4, можно выбрать в качестве ветвей дерева (рис. 1.21, 6); поэтому ветви с токами 1и 12 и 73 будут ветвями связи. На рис. 1.21, 6 элементы ветвей дерева изображены сплошными линиями, а элементы ветвей связи - штриховыми.

Для схем на рис. 1.21, а и б по первому закону Кирхгофа

На основании второго закона Кирхгофа для трех контуров, каждый из которых включает только одну ветвь связи,

Пользуясь уравнениями (1.41), исключим из уравнений (1.42) токи /4, /5 и /6 всех ветвей дерева, общих для нескольких контуров; в результате получим

В соответствии с уравнениями (1.43) можно принять, что каждый из токов I1и I2 и I3 замыкается через соответствующую ветвь связи в одном из контуров (рис. 1.21, а и б), и назвать такие токи контурными: Напряжения на резистивных элементах любого контура равны алгебраической сумме напряжений, обусловленных токами своего и смежных контуров. Например, в контуре из элементов r1, r5 и r4 разность ЭДС E1 - Е4 равняется сумме трех напряжений: от собственного контурного тока I1к на всех сопротивлениях этого контура и от токов I2к и IЗк соответственно на сопротивлениях r5 и r4. Токи в ветвях дерева, общих для нескольких контуров, равны алгебраическим суммам контурных токов:

Для этой же схемы можно получить и другие взаимно независимые уравнения. Например, выберем другое дерево из первой, пятой и шестой ветвей (рис. 1.21, в), так что вторая, третья и четвертая ветви будут ветвями связи, токи в которых совпадают с контурными. Применив в этом случае второй закон Кирхгофа для контуров 2-3-4-2, 3-1-2-4-3 и 2-4-1-2, получим уравнения с контурными токами I2к, I3к и I4к, замыкающимися через ветви деревьев по ветвям связи. Токи в ветвях дерева однозначно определяются через токи ветвей связи (совпадающие с контурными) по формулам

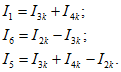
Выражение для тока I5 получено по первому закону Кирхгофа для токов в ветвях, примененному к главному сечению S5, след которого показан на рис. 1.21, в штриховой линией.
Таким образом, система взаимно не-зависимых уравнений определяется структурой выбранного дерева и соответствующими ветвями связи.
Схема рис. 1.21, а имеет 16 деревьев, поэтому для такой схемы можно написать 16 систем независимых уравнений, каждая из которых содержит в качестве неизвестных три тока, замыкающихся по ветвям связи через ветви выбранного дерева.
Из приведенных примеров следует, что для определения токов в ветвях этим методом нужно ввести в расчет контурные токи и решить совместно систему уравнений, составленных по второму закону Кирхгофа; число этих уравнений меньше числа неизвестных токов ветвей В на число узлов схемы без одного (У - 1). При замене токов в ветвях контурными токами первый закон Кирхгофа удовлетворяется для каждого узла, так как каждый контурный ток в одной из ветвей контура направлен к узлу, а в другой - от того же узла. Например, для узла 4 (рис. 1.21, а) по первому закону Кирхгофа для токов ветвей получим: , или для контурных токов .
Если схема содержит не только источники ЭДС, но и источники тока, то можно принять ток каждого из источников тока замыкающимся по любым ветвям дерева, составляющим с ветвью источника тока - ветвью связи - замкнутый контур. Падение напряжения, вызванное током такого источника на каждом из сопротивлений контура, учитывается при записи левой части уравнений по второму закону Кирхгофа. Эти напряжения можно также учесть с обратным знаком в правой части уравнений.
В качестве примера рассмотрим схему на рис. 1.17. На основании второго закона Кирхгофа

Пользуясь первым законом Кирхгофа, исключим из этих уравнений токи I5, I4 и I6; в результате после группировки слагаемых получим

Из этих уравнений следует, что в рассматриваемом случае ток J как бы замыкается по ветвям с сопротивлениями r5 и r4, дополняющими ветвь с источником тока J до замкнутого контура.
Обозначив в уравнениях (1.46) составляющие напряжений r4J и r5J соответственно через Eт4 и Ет5, можно переписать их иначе:

Здесь следует отметить, что перенос слагаемых r4J и r5J из левой в правую часть уравнений (1.47) и замена этих напряжений на схеме ЭДС Ет4 и Ет5 иллюстрируют применение так называемого принципа компенсации, изложенного более подробно в разделе.

Уравнениям (1.47) соответствует эквивалентная схема (рис. 1.22, а), на которой источник тока J заменен источниками ЭДС Ет4 = r4J и Ет5 = r5J, при этом токи в ветвях с сопротивлениями г4 и г5 не равны соответствующим токам в ветвях заданной схемы (см. рис. 1.17) и отличаются от них на ток J источника тока. Иначе говоря, после определения контурных токов I1к, I2к и I3к необходимо для вычисления токов I4 и I5 в ветвях заданной схемы (рис. 1.17) записать уравнения по первому закону Кирхгофа именно для заданной схемы:

Аналогично можно показать, что если принять ток J замыкающимся по ветви с сопротивлением r1, то получится новая эквивалентная схема (рис. 1.22, 6); контурный ток I1к в эквивалентной схеме не равен току I1 в ветви с сопротивлением r1 заданной схемы (см.рис. 1.17) и отличается от него на ток J.
Замена источника тока J двумя эквивалентными источниками напряжения Ет4 и Ет5 (рис. 1.22, а) основана на предварительном преобразовании одного источника тока, включенного к узлам 1 и 4 (см. рис. 1.17) двумя источниками тока, включенными к узлам 1 и 3, 3 и 4. Покажем справедливость такого преобразования для более общего случая.
На рис. 1.23, а изображена часть разветвленной схемы с одним источником тока J, присоединенным к узлам 1 и 4. Режим в этой схеме, очевидно, не изменится, если вместо одного источника тока J, присоединенного к выводам / и 4, включить три источника тока соответственно к узлам 1 и 2, 2 и 3, 3 и 4, поскольку токи 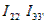. в ветвях присоединения к узлам 2 и 2', 3 и 3' равны нулю (рис. 1.23, 6). Переход от схемы рис. 1.23, б к эквивалентной схеме рис. 1.23, в, где уже не требует особых пояснений.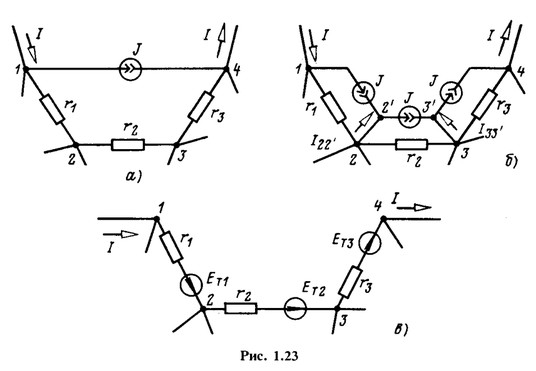

Таким образом, при расчете режима цепи методом контурных токов можно предварительно заменить источники тока эквивалентными источниками ЭДС, а затем ввести контурные токи и на основании второго закона Кирхгофа составить систему уравнений для их определения. Токи в ветвях без эквивалентных источников ЭДС, заменяющих источники тока, определяются по первому закону Кирхгофа суммированием контурных токов; в ветвях заданной схемы, в которых на эквивалентной схеме включены источники ЭДС, учитываются и токи источников тока.
При расчете электрических цепей изложенным методом всегда стремятся к тому, чтобы число контурных токов, замыкающихся через каждую из ветвей, было по возможности минимальным. С этой целью обычно выбирают каждый контур в виде ячейки (на рис. 1.21, а три ячейки с контурными токами I1к, I2к и I3к), руководствуясь указанным выше правилом выбора независимых контуров (дерева и ветвей связи) при составлении уравнений на основании второго закона Кирхгофа, что возможно для любой планарной схемы.
Положительные направления контурных токов можно выбирать и произвольно, т. е. независимо от положительных направлений токов в ветвях.
Установим теперь более общие, необходимые для дальнейших выводов соотношения между контурными токами, сопротивлениями и ЭДС цепи произвольной конфигурации.
Для схемы, имеющей К независимых контуров, уравнения, аналогичные (1.43), запишутся в виде

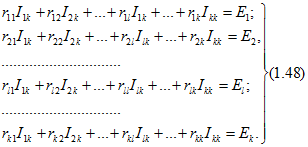
В этих уравнениях сопротивление вида ru (с двумя одинаковыми индексами) называется собственным сопротивлением контура l, а сопротивление вида (с двумя различными индексами) - общим сопротивлением контуров l и к. Правые части уравнений (1.48) называются контурными ЭДС. Каждая из контурных ЭДС вида Е1 равна алгебраической сумме ЭДС всех источников в ветвях контура l. Положительные знаки в каждом уравнении (1.48) должны быть взяты для токов и ЭДС, положительные направления которых совпадают с произвольно выбранным направлением обхода соответствующего контура.
В более общем случае для электрической цепи, которая содержит как источники ЭДС, так и источники тока, контурное уравнение для l-го контура записывается в виде

где обозначает собственное сопротивление контура l; - общее сопротивление двух контуров: l и j; - ток источника тока, замыкающийся по ветви с сопротивлением ; 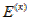- контурная ЭДС (алгебраическая сумма ЭДС в контуре).
Решив систему уравнений (1.48) при помощи определителей относительно любого из токов, например , получим

где - определитель системы уравнений (1.48), т. е.

алгебраические дополнения определителя , причем получается из путем вычеркивания l-го столбца и q-й строки и умножения полученного определителя на .
Необходимо отметить, что сопротивления вида нужно записывать в выражении (1.50) с тем знаком, который стоит перед соответствующим напряжением в уравнениях (1.48).
Методом узловых потенциалов целесообразно пользоваться, если число узлов схемы, уменьшенное на единицу, меньше числа независимых контуров У - 1 < К, а методом контурных токов - при У - 1 > К.

Матричные уравнения контурных токов.
Уравнения контурных токов (1.48) с учетом (1.48а) можно записать в матричной форме:

где - квадратная матрица контурных сопротивлений; - матрица-столбец контурных токов; - матрица-столбец контурных ЭДС, учитывающая источники ЭДС и эквивалентные ЭДС от источников тока.
После умножения уравнения (1.51) слева на получим

Покажем, что матрицу контурных сопротивлений можно получить непосредственно по схеме при помощи матрицы контуров В:

где r - диагональная матрица сопротивлений ветвей; - транспонированная матрица контуров.
Направление обхода каждого контура примем совпадающим с положительным направлением соответствующего контурного тока, а направления ветвей - с положительными направлениями токов в ветвях. Чтобы получить независимые контуры, следует сначала выбрать дерево схемы, что в свою очередь определяет ветви связи, а следовательно, и контурные токи.
Для иллюстрации рассмотрим схему на рис. 1.21, а с выбранным деревом из четвертой, пятой и шестой ветвей (рис. 1.21, 6). В этом случае независимые контуры содержат контурные токи I1к, I2к и IЗк, что соответствует первой, второй и третьей ветвям связи.
Матрица контуров В состоит из трех строк и шести столбцов:

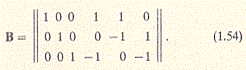
Диагональная матрица сопротивлений

Произведение матриц В и r равно:

Квадратная матрица контурных сопротивлений определяется по (1.53):

Матрица-столбец контурных токов

Матрица-столбец контурных ЭДС

Пользуясь уравнением (1.51), матрицами , можно получить уравнения (1.43).
Подчеркнем, что матрица токов ветвей I определяется через матрицу контурных токов по формуле

Например, для схемы рис. 1.21, а

Из этого матричного уравнения сразу получаем равенства, определяющие токи ветвей через контурные токи:

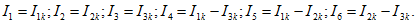
В дальнейшем индекс " к" у контурных токов, как правило, будем опускать.
В заключение подчеркнем, что все соотношения между токами ветвей и контурными токами для схем, показанных на рис. 1.21, а -в, можно получить из графов, построенных соответственно для этих схем на рис. 1.24, а-в, при этом деревья графа изображены на рис. 1.24, 6 и в толстыми линиями, а ветви связи - тонкими.

МЕТОД УЗЛОВЫХ ПОТЕНЦИАЛОВ

При расчете электрической цепи методом узловых потенциалов определяются потенциалы узлов цепи, а затем по закону Ома токи в ее ветвях. Метод целесообразно применять в тех случаях, когда число узлов цели меньше или равно числу независимых контуров этой цепи.
Так, для электрической цепи, имеющей четыре узла, составляется три расчетных уравнения (например, для узлов 1, 2 к 3 потенциал узла 4 принимается равным нулю):

где φ k - искомый потенциал K-го узла цепи (K = 1, 2, 3)
Gkk- (G11, например) собственная (узловая) проводимость k-го узла, равная сумме проводимостей всех ветвей, присоединенных к этому узлу;
Gkm -(G12, например) взаимная (межузловая) проводимость узлов k и m, равная суше проводимостей ветвей, включенных непосредственно между этими узлами;
Jyk (Jy1, например) - узловой ток к-го узла, определяемый из выражения

Под знаком первой суммы произведения ЭДС ветвей, присоединенных к К-му узлу, на проводимости этих ветвей учитывается ЭДС с положительным (отрицательным) знаком, если она направлена к К-му узлу (от К-го узла). Под знаком второй суммы со знаком «+» (" -" } учитываются токи источников тока, которые направлены к К-му узлу (от К-го узла).
Если в цепи между двумя узлами включен идеальный источник ЭДС (внутреннее сопротивление которого равно нулю), необходимо принимать равным нулю потенциал одного из его зажимов, тогда потенциал другого зажима источника будет равен ЭДС с
соответствующим знаком, а количество расчетных уравнений сократится.
Последовательность расчета цепи методом узловых, потенциалов рас-
смотрим на примере. Параметры цепи считаются заданными.

ПРИМЕР 1: Определить токи в ветвях цепи (рис. 1) методом
узловых потенциалов. Положительные направления токов принять по рисунку

E1=100В R1=10 Ом
E6=200В R2=20 Ом
I=5А R3 =5 Ом R4=25 Ом R5=40 Ом

1. В заданной цепи четыре узла. Приравняем нулю (заземлим) потенциал узла 4.Тогда ф4=0

2. Составим расчетную систему уравнений для узлов, потенциалы которых подлежат определению:

Для узлов 2 и 4 уравнения не составляются, так как потенциалы этих узлов известны.
3. Определим узловые и межузловые проводимости:

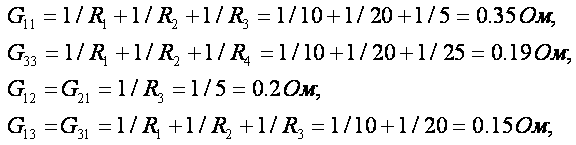
Взаимная проводимость между узлами 2 и 3 равна нулю, так как эти узлы непосредственно не связаны между собой какими-либо ветвями» т.е. G23=G32=0. Проводимость ветви с источником тока J также равна нулю, так как его внутреннее сопротивление бесконечно велико. Если в какой-либо ветви последовательно включено несколько резисторов, вначале определяется общее сопротивление этой ветви, а затем ее проводимость.
Определим узловые токи:

4. Подставим полученные значения узловых и межузловых проводимостей, а также узловых токов в расчетную систему уравнений. Решая ее, определим искомые потенциалы узлов цепи:

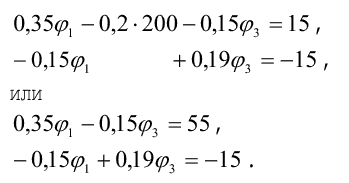
Решить систему уравнений можно методом определителей или с помощью микрокалькулятора по соответствующей программе, однако, если система содержит два уравнения, ее целесообразно решать домножением на общие множители:

*Запись выше несколько непонятна. Она означает домножение левой и правой частей уравнения на множители. Вообще необходимо любым способом решить систему уравнений: например, подстановкой.

Для проверки расчета целесообразно полученные значения потенциалов, вычисленные с точностью до 3-4 значащей цифры, подставить в исходную систему уравнений, которые при этом, очевидно, должны обратиться в тождества.
5. Используя закон Ома, определим токи в ветвях цепи.
Направления токов в ветвях выбраны произвольно и указаны на схеме (рис. I).
Составим выражение для разности потенциалов (напряжения) между узлами 3 и 1:

т.е. в дальнейшем при выбранном направлении тока в ветви его величина определяется следующим образом: в числителе выражения от потенциала узла, из которого ток вытекает, вычитается потенциал узла, к которому ток подтекает.
Если в ветви есть ЭДС, она учитывается со знаком «+» (" -" ), когда ее направление совпадает (противоположно) с направлением тока, В знаменателе выражения для тока находится суммарное сопротивление ветви. Аналогично определяются токи остальных ветвей:

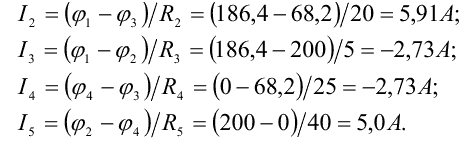
Значения токов I1, I2, и I4 получились со знаком «-». Это свидетельствует о том, что их направления в ветвях противоположны выбранным. Токи I3 и I4 равны между собой в силу принципа непрерывности электрического тока.
Ток в ветви с идеальной ЭДС Е6 определяется из уравнения, составленного по первому закону Кирхгофа. Например, для узла 2

6. Проверка расчета цепи выполняется по законам Кирхгофа
и уравнению энергетического баланса (балансу мощностей),
по первому закону Кирхгофа алгебраическая сумма токов в любом узле электрической цепи равна нулю. Проверяем выполнение этого закона для всех узлов цепи (кроме узла 2: из уравнения для этого узла определялся ток I6:

По второму закону Кирхгофа алгебраическая сумма ЭДС в любом замкнутом контуре электрической цепи равна алгебраической сумме падений напряжений на элементах этого контура. Проверяем выполнение этого закона дня всех независимых контуров заданной цепи;
Для контура с элементами Е1, R1 и R2

для контура с элементами R2, R3, R4 и R5

для контура с элементами E1, R3, E6, R4 и R1

Дня любой электрической цепи мощность, потребляемая резисторами этой цепи, должна равняться мощности источников энергии. Уравнение энергетического баланса ( баланс мощностей) в общем виде записывается следующим образом:

В левой части уравнения учтена мощность источников энергии. Мощность источников ЭДС учитывается с положительным (отрицательным) знаком, если ток, протекающий через источник ЭДС, совпадает ( противоположен) с направлением ЭДС.
Для определения знака мощности источника тока необходимо определить напряжение на источнике. Если ток источника вытекает из точки с меньшим потенциалом и подтекает к точке с большим потенциалом, мощность источника будет положительной (источник генерирует энергию). Если ток источника вытекает из точки более высокого потенциала по сравнению с потенциалом точки, куда ток втекает, мощность источника будет отрицательной, а режим его работы соответствует потреблению энергии.
В правой части уравнения энергетического баланса записывается арифметическая сумма мощностей, потребляемых резисторами цепи и определяемых по закону Джоуля-Ленца. По своему физическому смыслу эти мощности могут быть только положительными.
Для заданной электрической цепи (рис. I) уравнение энергетического баланса имеет вид

Расчет считается выполненным правильно, если расхождение между левой и правой частями уравнения электрического баланса не превышает 1...2%. Следует помнить, что при выполнении проверки расчета по законам Кирхгофа и балансу мощностей уравнения составляются по выбранным. В начале расчета положительным направлениям токов в ветвях заданной цепи, а числовые значения токов в уравнения подставляются со знаками, полученными в расчете.

10. Способы представления гармонических колебаний

Гармонические колебания можно представить несколькими способами. Рассмотрим эти способы.

Аналитический:

x = A sin ( ω t + φ ₀ ); υ _x = υ _m cos ( ω t + φ ₀ ); a_x = –a_m sin ( ω t + φ ₀ ).

Графический:

Геометрический, с помощью вектора амплитуды (метод векторных диаграмм):

Рассмотрим подробнее последний способ.

Пусть гармоническое колебание описывается уравнением x = A cos ( ω t + φ ₀ ). Проведем прямую Оx (опорную) и построим вектор , направленный из точки О под углом φ ₀ к опорной линии.

Обозначим через x₀ проекцию вектора на опорную линию в момент времени t = 0:

x₀ = A cos ( φ ₀ ).

Вращение происходит против часовой стрелки, т.е. ω > 0. За промежуток времени t вектор амплитуды повернется на угол ω t и займет новое положение. Его проекция на опорную линию равна x = A cos ( ω t + φ ₀ ).
За время, равное периоду колебаний Т, вектор амплитуды повернется на угол 2φ , и проекция вектора совершит полное колебание около положения равновесия (точка О). Следовательно, вращающийся вектор амплитуды полностью характеризует гармоническое колебание.

Проекция кругового движения на ось у также совершает гармоническое колебание y = A sin ( ω t + φ ).

Таким образом, равномерное движение по окружности можно рассматривать как два колебательных гармонических движения, совершаемых одновременно в двух взаимно перпендикулярных направлениях. Этим представлением широко пользуются при сложении колебаний.

Метод наложения

1.3.4. Метод наложения
В основе метода лежит принцип суперпозиции (наложения): ток в любой ветви сложной электрической цепи, содержащей несколько ЭДС, может быть найден как алгебраическая сумма токов в этой ветви от действия каждой ЭДС в отдельности.
Это весьма важное положение, справедливое только для линейных цепей, вытекает из уравнений Кирхгофа и утверждает независимость действия источников энергии. Основанный на нем метод сводит расчет цепи, содержащей несколько ЭДС, к последовательному расчету схем, каждая из которых содержит только один источник.
Например, токи в схеме на рис. 1.10, а находятся как алгебраические суммы частичных токов, определяемых из схем 1.10, б и в.

Аналогично:

12 3 4 5 6 7 8 9 10 Следующая ⇒