Модельные задачи и методы исследования устойчивости упругих систем
1. Метод Эйлера. Рассмотрим простую модельную задачу, которая поможет выяснить все особенности потери устойчивости. Пусть абсолютно жёсткий стержень (стойка) шарнирно опёрт на нижнем конце и закреплён с помощью упругой горизонтальной пружины на верхнем (рис. 9.10, а). Эта пружина отражает упругие свойства системы при поперечном отклонении. Реакцию пружины  представим соотношением:
представим соотношением:
 (9.3)
(9.3)
где  - горизонтальное перемещение верхнего конца стойки. Если перемещение
- горизонтальное перемещение верхнего конца стойки. Если перемещение  мало, то нелинейными членами можно пренебречь и принять
мало, то нелинейными членами можно пренебречь и принять 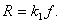 В противном случае задача принимает геометрически нелинейный характер.
В противном случае задача принимает геометрически нелинейный характер.
Нагрузим стойку вертикальной силой 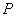 . Если подействовать на жёсткий стержень поперечной малой возмущающей силой
. Если подействовать на жёсткий стержень поперечной малой возмущающей силой 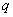 , то он отклонится на некоторый малый угол
, то он отклонится на некоторый малый угол  . Теперь снимем эту силу статически. Если стойка вернётся при заданном значении силы
. Теперь снимем эту силу статически. Если стойка вернётся при заданном значении силы 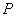 в исходное состояние, то она устойчива в смысле Эйлера, если не вернётся, то неустойчива. Пусть имеет место второй случай. Составим уравнение равновесия стойки:
в исходное состояние, то она устойчива в смысле Эйлера, если не вернётся, то неустойчива. Пусть имеет место второй случай. Составим уравнение равновесия стойки:
 (9.4)
(9.4)
где  - реакция упругой пружины.
- реакция упругой пружины.
Из (9.4) следует уравнение

откуда либо 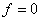 (устойчивость), либо
(устойчивость), либо  (неустойчивость). Пусть
(неустойчивость). Пусть  . Тогда в нуль обратится круглая скобка, что позволяет найти критическую силу
. Тогда в нуль обратится круглая скобка, что позволяет найти критическую силу
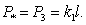 (9.5)
(9.5)
Полученное значение силы 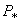 , при котором система впервые не возвратилась к исходному состоянию, называется бифуркационной нагрузкой Эйлера. При этом значении силы
, при котором система впервые не возвратилась к исходному состоянию, называется бифуркационной нагрузкой Эйлера. При этом значении силы 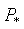 происходит нарушение единственности решения задачи
происходит нарушение единственности решения задачи 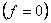 , т.е. бифуркация или ветвление решения. Вопрос о том, как будет вести себя стойка при
, т.е. бифуркация или ветвление решения. Вопрос о том, как будет вести себя стойка при 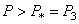 остаётся открытым.
остаётся открытым.
2. Метод Лагранжа. В основу этого метода положено динамическое определение устойчивости состояния равновесия Лагранжа. Для отклонённого состояния стойки, пользуясь принципом Даламбера, имеем (рис. 9.10, б):
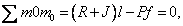 (9.6)
(9.6)
где 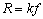 - упругая реактивная сила,
- упругая реактивная сила,  - сила инерции,
- сила инерции,  - прогиб,
- прогиб, 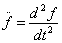 - ускорение,
- ускорение,  – масса груза на конце стойки.
– масса груза на конце стойки.

а) б)
Рис. 9.10
Из (9.6) находим уравнение колебаний системы с сосредоточенной массой  :
:
 (9.7)
(9.7)
Полагая  , получим характеристическое уравнение:
, получим характеристическое уравнение:
 (9.8)
(9.8)
где
 (9.9)
(9.9)
Если  , то
, то  ,
, 
 (9.10)
(9.10)
где  - круговая частота колебаний,
- круговая частота колебаний,  - начальная фаза,
- начальная фаза,  – амплитуда колебаний. Движение носит периодический характер и потому устойчиво. Если учесть внешнее и внутреннее сопротивление системы, то решение будет иметь вид
– амплитуда колебаний. Движение носит периодический характер и потому устойчиво. Если учесть внешнее и внутреннее сопротивление системы, то решение будет иметь вид
 ,
,
где  - параметр, определяющий сопротивление движений. Колебания с ростом времени
- параметр, определяющий сопротивление движений. Колебания с ростом времени  затухнут, и система вернётся в своё исходное состояние. Следовательно, исходное состояние равновесия устойчиво.
затухнут, и система вернётся в своё исходное состояние. Следовательно, исходное состояние равновесия устойчиво.
Если  , то
, то  – действительное число. Решение принимает вид:
– действительное число. Решение принимает вид:
 (9.11)
(9.11)
и носит апериодический, т.е. неустойчивый характер. При  имеем
имеем 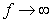 . При
. При  происходит переход от устойчивого периодического движения стойки к неустойчивому апериодическому. Это происходит при критической силе
происходит переход от устойчивого периодического движения стойки к неустойчивому апериодическому. Это происходит при критической силе 
Таким образом, динамический метод Лагранжа приводит к тому же результату, что и метод Эйлера.
3. Метод Кармана (начальных несовершенств). Т.Карман первым рассмотрел процесс продольного изгиба стойки с начальными несовершенствами как задачу устойчивости и трактовал предельную нагрузку не как исчерпания несущей способности системы, а как предел устойчивости. Однако такая точка зрения долгое время (вплоть до наших дней) не находила поддержки. Применим метод Кармана к стойке на рис. 9.11а.

а) б) в)
Рис. 9.11
Стойка имеет отклонение от вертикали на некоторый угол  и сжимается силой
и сжимается силой 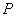 . При
. При  стойка отклонится от вертикали на угол
стойка отклонится от вертикали на угол  . Уравнение равновесия в некоторый момент процесса продольного нагружения стойки имеет вид
. Уравнение равновесия в некоторый момент процесса продольного нагружения стойки имеет вид
 (9.12)
(9.12)
где  Из (9.12) следует:
Из (9.12) следует:
 ,
,  (9.13)
(9.13)
Дифференцируя по  или по
или по 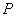 соответственно, находим:
соответственно, находим:
 (9.14)
(9.14)
откуда при  следует
следует  Согласно изложенной концепции значение силы
Согласно изложенной концепции значение силы  является пределом устойчивости и совпадает с эйлеровой силой.
является пределом устойчивости и совпадает с эйлеровой силой.
4. Энергетический метод С.П. Тимошенко. При отклонении системы на угол  от положения равновесия (рис. 9.11, в), верхний конец стержня опускается на величину
от положения равновесия (рис. 9.11, в), верхний конец стержня опускается на величину  . Сила
. Сила 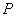 совершает работу
совершает работу  . Перемещение
. Перемещение

где прогиб 

Работа силы 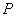 на перемещение
на перемещение  принимает вид
принимает вид 
Упругая внутренняя реактивная сила  совершает работу, называемую потенциальной энергией деформации:
совершает работу, называемую потенциальной энергией деформации:

Величина

носит название полной потенциальной энергии системы, связанной с потерей устойчивости. Если  (
(  ), то энергии
), то энергии  достаточно для возвращения стержня в исходное состояние, т.е. его состояние равновесия устойчиво. Если
достаточно для возвращения стержня в исходное состояние, т.е. его состояние равновесия устойчиво. Если  (
(  ), то энергии деформации недостаточно для возвращения стержня в исходное состояние равновесия, т.е. он находится в неустойчивом состоянии равновесия. Граничное значение энергии
), то энергии деформации недостаточно для возвращения стержня в исходное состояние равновесия, т.е. он находится в неустойчивом состоянии равновесия. Граничное значение энергии  является критерием для определения критической силы
является критерием для определения критической силы  . Таким образом, энергетический метод приводит к критической нагрузке, равной нагрузке Эйлера для данной модели.
. Таким образом, энергетический метод приводит к критической нагрузке, равной нагрузке Эйлера для данной модели.
5. Метод Койтера исследования нелинейного послебифуркационного процесса выпучивания (нагружения). Пусть реакция в упругой пружине (рис. 9.13):

 (9.15)
(9.15)
т.е. зависимость носит нелинейный характер.

а) б)
Рис. 9.13
Тогда уравнение равновесия (9.3) примет вид
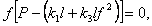 (9.16)
(9.16)
откуда либо 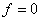 , либо
, либо  , и тогда равно нулю выражение в квадратной скобке. Второе условие приводит к соотношению, которое позволяет установить зависимость между силой
, и тогда равно нулю выражение в квадратной скобке. Второе условие приводит к соотношению, которое позволяет установить зависимость между силой 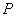 и перемещением
и перемещением  в процессе нагружения элемента:
в процессе нагружения элемента:
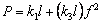 (9.17)
(9.17)
Если  , то имеем кривые зависимости с симметричной бифуркацией (рис. 9.13, а). Предположим, что с развитием выпучивания и увеличением перемещения
, то имеем кривые зависимости с симметричной бифуркацией (рис. 9.13, а). Предположим, что с развитием выпучивания и увеличением перемещения  в пружине при
в пружине при  возникают пластические деформации. Тогда вместо (9.3) при
возникают пластические деформации. Тогда вместо (9.3) при 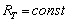 имеем:
имеем:


откуда
 (9.18)
(9.18)
и с ростом  нагрузка
нагрузка 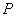 будет падать (рис. 9.13, а).
будет падать (рис. 9.13, а).
В реальных системах переход к пластической стадии деформирования осуществляется на графике 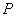 от
от  плавно с экстремальной предельной точкой.
плавно с экстремальной предельной точкой.
Если 
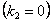 , то согласно (9.17) имеем симметричную неустойчивую бифуркацию, характерную для сжатых неупругих стержней и пластины (рис. 9.13, б).
, то согласно (9.17) имеем симметричную неустойчивую бифуркацию, характерную для сжатых неупругих стержней и пластины (рис. 9.13, б).
Пусть теперь
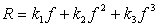 (
(  ).
).
Тогда, согласно (9.12), имеем:
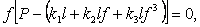
откуда при 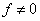 получаем:
получаем:
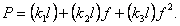 (9.19)
(9.19)
При 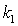 > 0,
> 0, 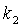 < 0,
< 0, 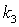 < 0 зависимость (9.19) имеет несимметричный вид (рис. 9.14, а). Прогибы
< 0 зависимость (9.19) имеет несимметричный вид (рис. 9.14, а). Прогибы  после бифуркации растут при падающей нагрузке. Такая точка бифуркации называется неустойчивой. Она характерна для упругих оболочек.
после бифуркации растут при падающей нагрузке. Такая точка бифуркации называется неустойчивой. Она характерна для упругих оболочек.
Если  > 0,
> 0, 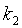 > 0,
> 0,  < 0, то бифуркация будет также несимметричной (рис. 9.14, б).
< 0, то бифуркация будет также несимметричной (рис. 9.14, б).
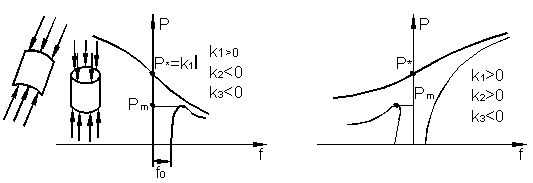
а) б)
Рис. 9.14
Популярное:

