Квантомеханическое описание частицы в бесконечно глубокой прямоугольной потенциальной яме.

⇐ ПредыдущаяСтр 10 из 10

Проведем качественный анализ решений уравнения Шредингера применительно к частице в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками». Такая «яма» описывается потенциальной энергией вида (для простоты принимаем, что частица движется вдоль оси х) где l — ширина «ямы», а энергия отсчитывается от ее дна.

Уравнение Шредингера для стационарных состояний в случае одномерной задачи запишется в виде

. На границах «ямы» (при х = 0 и х = l) непрерывная волновая функция также должна обращаться в нуль. Следовательно, граничные условия в данном случае имеют вид

Общее решение дифференциального уравнения: Так как 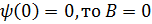. Тогда 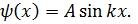Условие выполняется только при где п — целые числа, т. е. необходимо, чтобы . Cледует, что т. е. стационарное уравнение Шредингера, описывающее движение частицы в «потенциальной яме» с бесконечно высокими «стенками», удовлетворяется только при собственных значениях , 'зависящих от целого числа п. Следовательно, энергия £ „ частицы в «потенциальной яме» с бесконечно высокими «стенками» принимает лишь определенные дискретные значения, т. е. квантуется. Квантованные значения энергии называются уровнями энергии, а число п, определяющее энергетические уровни частицы, называется главным квантовым числом. Таким образом, микрочастица в «потенциальной яме» с бесконечно высокими «стенками» может находиться только на определенном энергетическом уровне £ „, или, как говорят, частица находится в квантовом состоянии п.

Излучение и поглощение электромагнитной волны. Спонтанное и вынужденное излучение. Резонансное поглощение. Ширина спектральной линии. Коэффициенты Эйнштейна.

Излучение и поглощение электромагнитной волны.

Электромагнитное излучение (электромагнитные волны) — распространяющееся в пространстве возмущение (изменение состояния) электромагнитного поля (то есть, взаимодействующих друг с другом электрического и магнитного полей).

Некоторые особенности электромагнитных волн c точки зрения теории колебаний и понятий электродинамики:

наличие трёх взаимно перпендикулярных (в вакууме) векторов: волнового вектора, вектора напряжённости электрического поля E и вектора напряжённости магнитного поля H.

электромагнитные волны — это поперечные волны, в которых вектора напряжённостей электрического и магнитного полей колеблются перпендикулярно направлению распространения волны, но они существенно отличаются от волн на воде и от звука тем, что их можно передать от источника к приёмнику в том числе и через вакуум.

Распространение электромагнитных волн, временные зависимости электрического 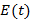и магнитного полей, определяющий тип волн (плоские, сферические и др.), вид поляризации и прочие особенности зависят от источника излучения и свойств среды.

Электромагнитные излучения различных частот взаимодействуют с веществом также по-разному. Процессы излучения и поглощения радиоволн обычно можно описать с помощью соотношений классической электродинамики; а вот для волн оптического диапазона и, тем более, жестких лучей необходимо учитывать уже их квантовую природу.

Спонтанное и вынужденное излучение.

Вынужденное излучение, индуцированное излучение — генерация нового фотона при переходе квантовой системы (атома, молекулы, ядра и т. д.) из возбуждённого в стабильное состояние (меньший энергетический уровень) под воздействием индуцирующего фотона, энергия которого была равна разности энергий уровней. Созданный фотон имеет те же энергию, импульс, фазу и поляризацию, что и индуцирующий фотон (который при этом не поглощается). Оба фотона являются когерентными.

Спонтанное излучение или спонтанное испускание — процесс самопроизвольного испускания электромагнитного излучения квантовыми системами (атомами, молекулами) при их переходе из возбуждённого состояния в стабильное.

Резонансное поглощение.

Поглощение фотонов частоты v, где и - энергии возбуждённого и основного состояний поглощающей системы (напр., атома), h - Планка постоянная. Резонансное поглощение наблюдается и в ядерной физике.

Ширина спектральной линии.

Ширина спектральных линий, интервал частот v (или длин волн , с — скорость света), характеризующий спектральные линии в спектрах оптических атомов, молекул и др. квантовых систем. Каждому излучательному квантовому переходу между дискретными уровнями энергии и соответствует некоторый интервал частот, близких к частоте перехода . Значение определяет ширину спектральной линии. ¾ степень немонохроматичности данной спектральной линии. Контур спектральной линии j(n) [зависимость интенсивности испускания (поглощения) от частоты] обычно имеет максимум при частоте перехода или вблизи неё; за Ш. с. л. принимают разность частот, которым соответствует уменьшение интенсивности вдвое (её называют иногда полушириной спектральной линии). Если не учитывать Доплера эффект, Ш. с. л. определяется суммой ширин уровней энергии и

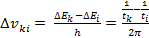, т. е. тем больше, чем меньше времена жизни и . Радиационная (естественная) Ш. с. л. соответственно равна: (где и — полные вероятности спонтанных переходов с уровней и на все нижележащие уровни); она очень мала и обычно Ш. с. л. для атомов и молекул определяется в основном уширением их уровней энергии при взаимодействии с окружающими частицами (в газе и плазме — при столкновениях), а также уширением спектральных линий вследствие эффекта Доплера. В зависимости от типа уширения получается симметричный или асимметричный контур спектральных линий (на рис. показан симметричный, т. н. дисперсионный, контур, характерный для радиационного уширения).

Коэффициенты Эйнштейна.

Эйнштейна коэффициенты характеризуют вероятности излучательных квантовых переходов. Были введены Альбертом Эйнштейном в 1916 при построении теории испускания и поглощения излучения атомами и молекулами на основе представления о фотонах; при этом им впервые была высказана идея существования вынужденного излучения. Вероятности спонтанного испускания, поглощения и вынужденного испускания характеризуются соответственно коэффициентами , и (индексы указывают на направление перехода между верхним и нижним уровнями энергии). Соотношения между Эйнштейна коэффициенты были впервые получены Эйнштейном при выводе Планка закона излучения путём рассмотрения термодинамического равновесия вещества и излучения.

Пусть — вероятность вынужденного перехода атома в единицу времени с энергетического уровня на уровень 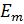, а

— вероятность обратного перехода. Выше было указано, что при одинаковой интенсивности излучения = . Вероятность вынужденных переходов пропорциональна плотности энергии «и вынуждающего переход электромагнитного поля), приходящейся на частоту , соответствующую данному переходу .Обозначив коэффициент пропорциональности буквой В, получим

. В е л и ч и н ы и н а з ы в а ю т с я к о э ф ф и ц и е н т а м и Э й н ш т е й н а. Согласно сказанному выше = . Основываясь на равновероятности вынужденных переходов п-т и т-п, Эйнштейн дал весьма простой вывод формулы Планка. Равновесие между веществом и излучением будет достигнуто при условии, что число атомов , совершающих в единицу времени переход из состояния п в состояние т, будет равно числу атомов , совершающих переход в обратном направлении. Допустим, что .Тогда переходы т-п смогут происходить только под воздействием излучения. Переходы же m-n будут совершаться как вынужденно, так и спонтанно.

⇐ Предыдущая 1 2 3 4 5 6 7 8 910