
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Г.П. Стародубцева, А.А. Хащенко, Г.Е. Ковалёва
Г.П. Стародубцева, А.А. Хащенко, Г.Е. Ковалёва
ЛАБОРАТОРНЫЙ ПРАКТИКУМ По механике и молекулярной Физике
Учебное пособие для студентов, обучающихся по специальностям: «Механизация сельского хозяйства», «Сервис транспортных средств и технологического оборудования в АПК» СТАВРОПОЛЬ УДК ББК
Печатается по рекомендации методической комиссии факультета механизации СХ СтГАУ (протокол № 6 от 18 февраля 2011)
Рецензенты:
Г.П. Стародубцева, А.А. Хащенко, Г.Е. Ковалева. Лабораторный практикум по механике и молекулярной физике. Учебное пособие для студентов аграрных, обучающихся по специальностям: шифр Механизация сельского хозяйства, Сервис транспортных средств и технологического оборудования в АПК – Ставрополь: Изд.-во 2011 – 70 с.
В пособии даны описания выполнения девяти лабораторных работ разделу «Механика и молекулярная физика», а также вопросы для защиты лабораторных работ. Минимально необходимые теоретические сведения из математики, а также значения некоторых физических величин, приведены в приложениях. Предназначен для студентов аграрных вузов, обучающихся по специальностям «Механизация сельского хозяйства» и «Сервис транспортных средств и технологического оборудования в АПК». Может быть использовано в качестве учебного пособия студентами, обучающимися на других инженерных специальностях аграрных вузов.
УДК ББК
© Г.П. Стародубцева, А.А Хащенко, Г.Е. Ковалева, 2011.
ВВЕДЕНИЕ
Данный практикум включает в себя 9 лабораторных работ по механике и молекулярной физике, отвечающих требованиям рабочей программы для студентов факультета шифр Механизации сельского хозяйства. К каждой работе даны: краткая теория по исследуемому физическому явлению; рисунок или схема, описание приборов, установки; порядок выполнения и оформления работы; литература. Большинство лабораторных работ носит исследовательский характер. В их включены вопросы для самоконтроля, справочные материалы и таблицы, необходимые для выполнения лабораторных работ. Введение содержит элементы теории погрешностей, примеры вычисления погрешностей, рекомендации по статистической обработке результатов экспериментов и графические методы обработки результатов измерений. Перед выполнением лабораторной работы студент должен предварительно подготовиться к ней, используя данное пособие, записать в тетрадь название работы, цель работы, краткую теорию, основные рабочие формулы и оформить таблицы результатов измерений и вычислений. Также необходимо ответить на контрольные вопросы, используя рекомендуемую литературу В аудитории, получив допуск к работе, студент должен провести опыты, по полученным данным рассчитать требуемые величины, погрешности измерений, заполнить таблицы, построить графики и сделать выводы.
ТЕОРИЯ ПОГРЕШНОСТЕЙ
Цель любого исследования – установление связи между различными явлениями и параметрами. Количественная зависимость между исследуемыми величинами получается в результате измерений. Измерение – это нахождение значения физической величины опытным путем техническими средствами. Результат измерений следует выражать в СИ. Всякое значение, полученное в результате измерений, дает лишь приближенное значение измеряемой величины. Если систематические и грубые ошибки измерений могут быть учтены и устранены, то случайные погрешности неизбежны как в каждом определении, так и в величине среднего значения, вычисленного из отдельных определений. Поэтому необходимо уметь рассчитывать возможные погрешности и представлять результаты измерений с учетом их достоверности. Измерения называются прямыми, если определяемая величина непосредственно сравнивается с эталоном меры (измерение длины, времени, массы и т.д.). Чаще производят не прямые измерения данной величины, а косвенные - через другие величины, связанные с измеряемой определенной математической зависимостью. Например, плотность тела определяется по измерениям массы и объема. Погрешности, допускаемые во время измерений, делятся на две категории: систематические и случайные. Систематические погрешности - погрешности, связанные с ограниченной точностью изготовления прибора (неравноплечность коромысла весов), неточностью самого метода измерения (пренебрежение силами сопротивления и трения), неправильной установки прибора (например, сбит ноль шкалы прибора), но эти погрешности можно исключить, введя соответствующие поправки. Для этого приходится периодически проводить проверку приборов по эталонным. Случайные погрешности - вызываются большим числом случайных причин, действие которых на результат каждого измерения различно и они не могут быть заранее учтены. Случайные погрешности могут быть вызваны случайными сотрясениями здания, влиянием незначительного движения воздуха, трением подвижных элементов приборов и переносятся в разной мере и с разным знаком из опыта в опыт. Математическая теория случайных величин (математическая статистика) позволяет уменьшить влияние этих погрешностей на конечный результат и установить величину погрешности измерений. Для этого необходимо провести не одно измерение, а несколько. Теория ошибок дает возможность выбрать разумное число измерений для обеспечения данной точности.
ЭЛЕМЕНТЫ ТЕОРИИ ПОГРЕШНОСТЕЙ Пусть имеется некоторая случайная величина Х, которая может принимать ряд из п произвольных значений. Их можно наглядно представить, построив диаграмму, которая показывала бы, как часто использовались при измерениях те или иные значения. Для этого диапазон значений, отложенных по оси ОХ, разбивают на равные интервалы шириной Существуют различные виды распределения случайных величин, однако особое значение имеет нормальный закон распределения случайной величины (закон Гаусса), для которого функция распределения вероятностей описывается формулой где Зная закон распределения нормальной погрешности, можно провести вероятностную оценку погрешности измерения. Допустим, что при определении неизвестной величины А нами получен ряд из п отдельных измерений Х1, Х2,..., Хп, средняя арифметическая которых равна Каждое отдельное измерение и среднее из всех измерений, имеют свои погрешности. Абсолютной ошибкой ε приближенного значения некоторой величины называют разность между точным и приближенным значениями этой величины.
Относительной ошибкой Относительную ошибку приближенных значений принято выражать в процентах. Вместо точного значения величины А, которое нам не известно, в формулы 2-3 подставляют среднее значение экспериментальных данных, т.е. величину М, или, если оно известно, табличное значение определяемой величины А.
СРЕДНЯЯ АБСОЛЮТНАЯ ОШИБКА При достаточно большом количестве проведенных исследований случайной величины (по крайней мере, больше десяти), достоверную величину погрешности измерений отражает средняя абсолютная ошибка
СРЕДНЯЯ КВАДРАТИЧНАЯ ОШИБКА При малом числе проведенных измерений (три - пять) для достоверной оценки погрешностей вычисляют средний квадрат абсолютных ошибок Величина Между величинами
СРЕДНЯЯ КВАДРАТИЧнАЯ ОШИБКА СРЕДНЕГО Средняя квадратичная ошибка
В итоге вычислений результат измерений записывается в виде
Относительная ошибка измерений, выраженная в процентах, будет равна
Рассмотрим пример: Вычислить среднее и его ошибку для ряда чисел -10, 11, 12, 13, 14, 15, 16, 17, 18.
N=9; M=
Или Далее
Из примера видно, что величины средней квадратичной ошибки среднего, вычисленные по формуле и через среднюю абсолютную ошибку, отличаются друг от друга. Следовательно, принимая второй путь расчета, как более простой, мы незначительно увеличиваем оцениваемые ошибки среднего значения. Удобство оценки погрешности измерений с помощью средней квадратичной погрешности заключается в том, что
Интервал значений измеряемой величины от Доверительную вероятность погрешности среднего арифметического значения можно также найти из Приложения 1. Приведенные в Приложении 1 формулы справедливы только для большого числа измерений, что не всегда возможно. В случае небольшого количества измерений (n< 30) задают доверительную вероятность p по таблице приложения 2, находят значение коэффициента Стьюдента t для данного числа измерений n. Определив t по таблице приложения 2, находят случайную погрешность Рассмотрим пример: Пусть в результате четырех измерений x получены следующие значения: 2, 80; 2, 79; 2, 84; 2, 83. Найдем их среднее арифметическое значение. Средняя квадратичная погрешность отдельного измерения
Средняя квадратичная погрешность среднего значения Зададим доверительную вероятность p=0.95. По таблице приложения 2 находим значения коэффициента Стьюдента при n=4 и p=0, 95: t=3, 2. Величину случайной погрешности
ПОГРЕШНОСТИ КОСВЕННЫХ ИЗМЕРЕНИЙ Пусть определяемая величина y является функцией нескольких независимо измеряемых величин
Известно, что полный дифференциал функции y определяется по формуле
При малых значениях дифференциала аргумента
В теории ошибок формулируется закон сложения погрешностей, согласно которому для нахождения суммарной погрешности нужно складывать не сами погрешности, а их квадраты. Учитывая этот закон, а также формулу (12), получаем соотношение для нахождения средней абсолютной погрешности измерения величины y
Аналогично определяется средняя квадратичная погрешность:
Относительная погрешность искомой величины вычисляется по формуле Так как Рассмотрим несколько примеров: 1. Искомая величина является суммой или разностью двух независимых измеряемых величин:
2. Искомая величина является произведением нескольких независимо измеряемых величин:
Средняя квадратичная погрешность 3. Искомая величина является частным от деления двух независимо измеряемых величин: Погрешность Средняя квадратичная погрешность Относительная погрешность Рассмотрим пример: Пусть при определении объема V цилиндра в результате 5 измерений высоты h цилиндра и диаметра D его основания были получены следующие значения:
По формуле
Найдя из Приложения 2 значение параметра t=2, 8, определим доверительный интервал Окончательный результат запишем в виде V=(237±20) см3 (p=0, 95).
ТОЧНОСТЬ ИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ Точностью измерительного прибора называется наименьшая величина, которую можно вполне надежно определять с помощью данного прибора. Если точность прибора неизвестна, ее считают равной половине цены наименьшего деления шкалы прибора. Если измерения проводятся прибором, снабженным нониусом (штангенциркуль), то точность прибора принимается равной разности между ценой одного деления прибора и одного деления нониуса. Для электроизмерительных приборов погрешность измерения характеризуется классом точности в пределах от 0, 05 до 4. Значение класса точности указывается на лицевой стороне прибора. Штангенциркуль (рис. 1, а, б) Состоит из подвижной и неподвижной измерительных губок 2, 3 и имеет две шкалы: (см. рис. 1, а): основная 1 и шкала 4 нониуса. Цена деления основной шкалы - 1мм, нониуса – 0, 9 мм (см. рис. 1, б), таким образом, каждое деление нониуса короче деления штанги на 0, 1 мм. точностью нониуса называется отношение цены деления шкалы основной линейки к числу делений нониуса. Чтобы измерить линейный размер предмета, его зажимают между измерительными губками штангенциркуля и делают отсчет по нониусу. Если нулевое деление нониуса совпадает с каким-нибудь делением шкалы (на штанге), то это деление указывает действительный размер в мм. Если нулевое деление нониуса не совпадает ни с одним делением основной шкалы, то действительный размер равен сумме двух слагаемых: целому числу миллиметров, сложенному с дробной частью. Целое число миллиметров
показывает ближайший штрих основной шкалы слева от нулевого штриха нониуса, а число десятых долей миллиметра равно порядковой цифре штриха нониуса, который точно совпал со штрихом основной шкалы (штанги). Микрометр (рис. 2, а, б) представляет собой массивную металлическую скобу 8, с одной стороны которой имеется неподвижная измерительная пятка, с другой – стебель 2, снаружи охватываемый барабаном 4, соединенный с микрометрическим винтом 7. На правом конце стебля микрометра имеется трещотка, предназначенная для обеспечения постоянства измерительного усилия. На поверхность стебля микрометра нанесена продольная риска, вдоль которой (выше и ниже ее) нанесены миллиметровые штрихи 3.
а б Рисунок 2. Микрометр: а) общий вид, б) шкала барабана
Верхние штрихи делят нижние пополам. Эта шкала называется основной. Вторая шкала нанесена на окружность скоса барабана и называется круговой шкалой 4. Цена деления основной шкалы – 1мм, круговой шкалы -0, 01 мм. Показания микрометра складываются из показаний основной шкалы и шкалы барабана (см. рис. 2 б). Порядковый номер видимого нижнего штриха основной шкалы перед кромкой барабана равен целому числу миллиметров. Если перед кромкой барабана виден еще и штрих сверху, то к числу миллиметров нужно прибавить еще 0, 5 мм. Число сотых долей миллиметра равно порядковому номеру штриха на шкале барабана, совпадающего с продольным штрихом шкалы.
Лабораторная работа № 1
МАТЕМАТИЧЕСКИЙ МАЯТНИК
Цель работы: изучение свободных колебаний маятника, определение ускорения свободного падения. Оборудование: лабораторная установка, секундомер.
Теоретическое введение
Математическим маятником называется тело, подвешенное на длинной невесомой нити, длина которой во много раз превышает линейные размеры тела (рис. 1). Период колебаний математического маятника определяется по приближенной формуле, пригодной только для малых амплитуд колебаний:
где: I - момент инерции маятника относительно оси колебаний, m - масса маятника, d - расстояние от оси до центра масс маятника, в данном случае равное длине нити маятника l, g - ускорение свободного падения. Математический маятник представляет собой механическую колебательную систему, колебания в которой происходят под действием квазиупругой силы: где: k – коэффициент жесткости колебательной системы, х – смещение системы от положения равновесия. Система, движущаяся под действием квазиупругой силы, называется одномерным гармоническим осциллятором. Уравнение второго закона Ньютона, для одномерного гармонического осциллятора можно записать в виде
Так как а= x″, то уравнение (1) можно преобразовать к виду mx″ + kx = 0 (3) Разделив все члены уравнения на m, и с учётом того, что собственная частота колебаний системы, получим уравнение движения одномерного гармонического осциллятора:
Его решение имеет вид: x = A cos (ω 0t +φ 0 ), (5) где: A – амплитуда колебаний, φ 0 – начальная фаза колебаний В настоящей работе проводится проверка соотношения (1) в случае, когда маятник можно приближенно считать математическим, т.к. масса маятника сосредоточена в области, размеры которой малы по сравнению с длиной маятника. Исследуемый в данной работе маятник представляет собой стальной шарик радиусом R на бифилярном подвесе, тонкая нить проходит через центр масс шарика. Длина подвеса может регулироваться, период колебаний маятника с высокой точностью измеряется электронным секундомером (рис. 1). Пренебрегая моментом инерции нити, ввиду его малости, запишем момент инерции маятника по теореме Штейнера:
В первом приближении, с учетом того, что l > > R можно получить I =m l 2 (7) С учетом (7) период колебания маятника можно записать в виде: . Из (5) можно найти выражение для ускорения свободного падения
Экспериментальная часть Соотношение (9) позволяет опытным путем определить ускорение свободного падения. Для этого необходимо измерить период колебания маятника Т и длину подвеса l. Но прежде необходимо выяснить, применимо ли соотношение (9) для лабораторной установки. Так как соотношение (1) справедливо для идеализированной модели физического маятника, то и соотношение (9) справедливо только в рамках этой модели. При выводе соотношения (1) были сделаны следующие предположения: - маятник совершает колебания с малой амплитудой; - затуханием колебаний можно пренебречь. 1. Определите период колебания маятника при различных значениях амплитуды в пределах Таблица 1
2. Проверьте, подтверждается ли на опыте линейная зависимость между квадратом периода колебаний и длиной маятника. Для этого измерьте период колебания маятника для четырех – пяти длин подвеса в пределах от lmin до lmax..0 При измерениях амплитуда колебаний должна быть малой. Результаты измерений занесите в таблицу 2 Таблица 2
3. По результатам измерений постройте график зависимости квадрата периода колебаний от длины маятника в координатах (l, 4. Определите ускорение свободного падения и оцените погрешность измерения.
Вопросы к защите работы: 1. Что называется математическим маятником? 2. От чего зависит период колебаний математического маятника? 3. Приведите вывод рабочей формулы. 4. Какие колебания называются гармоническими? 5. Выведите дифференциальное уравнение, описывающее гармонические колебания. Каково его решение?
Лабораторная работа № 2 ФИЗИЧЕСКИЙ МАЯТНИК Цель работы: изучение свободных колебаний физического маятника. Оборудование: тонкий стержень, секундомер. Теоретическое введение
Моментом инерции I материальной точки относительно оси вращения называется скалярная величина равная произведению массы точки на квадрат ее расстояния от оси вращения. Моментом инерции системы материальных точек относительно некоторой оси называется величина равная Твердое тело можно рассматривать как систему материальных точек, взаимное расположение которых не изменяется ни при каких условиях. Поэтому момент инерции твердого тела может быть определен как величина равная сумме моментов инерции материальных точек
Для определения момента инерции твердого тела относительно некоторой оси, не проходящей через центр масс, используется теорема Гюйгенса – Штейнера
где: m – масса тела, d – расстояние между осями (рис. 1). Одним из наиболее простых методов определения момента инерции твердого тела является метод физического маятника. Физическим маятником называется твердое тело способное совершать колебания относительно оси, не проходящей через центр масс (рис. 2). При отклонении маятника от положения равновесия на угол
   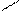 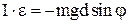 . (5) . (5)
   В теории принято рассматривать так называемые малые колебания, при которых можно считать, что В теории принято рассматривать так называемые малые колебания, при которых можно считать, что 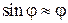 . Тогда учитывая, что . Тогда учитывая, что 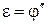 уравнение можно переписать в виде: уравнение можно переписать в виде:  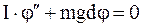 . (6) . (6)
Разделив обе части уравнения (5) на I получим: Сравнивая уравнение (6) с уравнением гармонического осциллятора которое описывает гармонические колебания с частотой
Уравнение (8) и соотношение (9) являются достаточно точными для малых амплитуд колебаний. Это решение для уравнения (8) является точным, но годится лишь для малых амплитуд. В данной работе проводится экспериментальная проверка соотношения для физического маятника, имеющего форму стержня. Стержень может колебаться относительно горизонтальной оси (рис. 2). Момент инерции I стержня длиной L и массой m, относительно оси О может быть найден с помощью теоремы Штейнера.
где Тогда для периода колебаний стержня можно получить
Введя обозначения
Величина В этой работе необходимо изучить зависимость периода колебаний тонкого однородного стержня от расстояния d от оси подвеса до центра масс. Результаты измерений удобно изобразить графически на координатной плоскости (
График этой зависимости необходимо построить по точкам, рассчитав Экспериментальная часть
1. Измерьте длину стержня L. 2. Рассчитайте величину 3. Рассчитайте теоретическую зависимость 4. Подвесив стержень в точке О, определите время t в течение которого маятник совершает 30-50 колебаний и рассчитайте период колебаний Т маятника относительно точки О. Опыт проделайте не менее трех раз и найдите среднее значение периода колебаний. 5. Рассчитайте величину 6. Измерьте расстояние d от оси вращения до центра масс и определите величину 7. Опыт повторите, подвешивая стержень в точке 8. Нанесите экспериментальные данные на график теоретической зависимости и сделайте вывод.
Вопросы к защите работы: 1. Что называется моментом инерции материальной точки? Твердого тела? 2. Запишите моменты инерции тел правильной геометрической формы. 3. Сформулируйте теорему Штейнера. 4. Что называется физическим маятником? 5. От чего зависит период колебаний физического маятника? 6. Что называется приведенной длиной физического маятника? 7. Приведите вывод рабочей формулы.
Лабораторная работа № 3
ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ Цель работы: экспериментальная проверка основного уравнения динамики вращательного движения и определение момента инерции диска. Оборудование: экспериментальная установка, секундомер.
Теоретическое введение
Движение тела, вращающегося вокруг неподвижной оси, описывается основным уравнением динамики вращательного движения
где: I - момент инерции тела относительно той же оси,
M - суммарный момент сил, действующих на тело. Популярное:
|
Последнее изменение этой страницы: 2016-08-31; Просмотров: 470; Нарушение авторского права страницы