
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Геометрия и кинематика червячного зацепления.
Диаметр делительного цилиндра червяка: где
Диаметры окружностей вершин и впадин червяка где Червячное колесо является косозубым с углом наклона линии зуба Межосевое расстояние Длина b1 нарезной части червяка принимается такой, чтобы обеспечить зацепление с возможно большим числом зубьев колеса. Передаточное отношение червячной передачи U= Если передача со смещением(корригированная) то, высота головок зубьев: высота ножек: Делительный диаметр червяка Межосевое расстояние Модуль Где x - коэффициент смещения При работе передачи в зоне контакта червячной пары возникает скольжение с большими скоростями, что обуславливает снижение коэффициента полезного действия передачи, повышение скорости изнашивания рабочих поверхностей элементов червячной пары и их склонность к заеданию. Окружная скорость вращения червяка Vs= Проектный расчет на контактную выносливость Допускаемое контактное напряжение:
Допускаемые напряжения изгиба:
где
где
где
Проверочный расчет на контактную и изгибную выносливость зубьев червячного колеса Расчетное контактное напряжение:
где
где
где
Недогрузка составляет:
Расчетное напряжение изгиба:
где
где
Если
Тепловой расчет червячной передачи, КПД, смазывание червячной передачи. Повышенная тенденция к нагреванию из-за скорости скольжения. Из уравнения теплового баланса можно опр. раб. темп. червячной передачи:
P1-передаваемая мощность (на червяке) η - КПД червячной пары Кт- коэффициент теплопередачи А- поверхность охлаждения [t]≤ 70…75 –при верх. черв. ≤ 80…90- при нижнем черв. При неудв. тепловом расчете устанавливают ребра; вентилятор; на валу червяка змеевик с холодной водой. Червяки бывают 1-но, 2-х и 4-х заходные. Чем больше число заходов, тем выше КПД q – коэф. диаметра червяка
При верхнем расположении червяка: При V 1…2 м/с червячное колесо может погрузится до ½ R черв. колеса. При V> 2 погружается на высоту зуба hm=2.2m При нижнем расположении червяка: Погружают червяк на высоту зуба, но при этом уровень масла не выше середины нижнего тела качения в противном случае устанавливаются брызговики
Силы в зацеплении. Статика передачи. При определении сил полагают, что главный вектор (равнодействующая) Fn контактных давлений, действующих на площадках контакта зубьев, приложен в полюсе П и направлен по линии зацепления (рис. 2.3) Окружная сила на колесе:
Окружная сила на червяке:
Радиальная сила:
где
Вращающий момент на колесе при ведущем червяке
Рис. 2.3. Усилия в червячной передаче
Валы и оси Общие сведения. Материал. Проектный расчёт. Проверочный расчёт на статическую прочность и выносливость валов. Переходные (от одного диаметра к другому) участки вала оформляются галтелью, канавкой для выхода шлифовального круга.Такие участки наз-ся концентраторами напряжений. 1. увеличение радиуса галтели 2. протачиванием разгрузочных канавок 3. деформационное упрочнение (наклёп) Передача нагрузок на вал от детали передаются: 1. крутящий момент (Т) – через шпонку, шлицы, посадку натягом, торцевые участки вала делают коническими (для простоты сборки – разборки) 2. радиальная сила передаётся непосредственно контактом ступицы детали на вал 3. осевые силы передаются упором в уступы на валу натягом гайками, стопорными пружинами, кольцами. Критерии работоспособности: прочность и жёсткость. Статическая прочность обеспечивается коэф. запаса Sт, а циклическая прочность S. Жёсткость обеспечивается прогибом f, углом поворота Q, крутильная жёсткость Валы относятся к числу наиболее ответственных деталей машин. Для обеспеченияработоспособности они должны удовлетворять условиям прочности и жёсткости. Расчёт валов на прочность состоит в оценке напряжений, возникающих всечениях вала от действия постоянных и переменных нагрузок. Эти нагрузкипередаются от установленных на вал деталей - зубчатых колёс, звёздочек цепныхпередач, шкивов ремённых передач. Возникающая в зубчатом зацеплении сила взаимодействия с сопряжённым колесомнаправлена по линии зацепления, как по общей нормали к рабочим поверхностямконтактирующих зубъев. Момент этой силы относительно оси вала равен действующемувращающему моменту Т. Для удобства расчётов силу взаимодействия раскладывают насоставляющие. Этими составляющими являются: - для прямозубой и шевронной цилиндрических передач - окружная Ft ирадиальная Fr силы. Первая направлена по касательной к начальной окружностиколеса, вторая- от точки зацепления по радиусу колеса к центру (рис. 23, а): Ft=2T/d; Fr = Ft tg 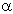 - для прямозубой, Fr=Ft tg - для прямозубой, Fr=Ft tg 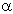 /cos /cos  - для шевронной передачи, где - для шевронной передачи, где 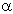 - угол зацепления, для некоррегированных колёс принимают равным 20°, d- диаметр делительной окружности колеса, - угол зацепления, для некоррегированных колёс принимают равным 20°, d- диаметр делительной окружности колеса,  - угол наклона зубъев; - для косозубой цилиндрической передачи - окружная Ft, осевая Fa, направленная от точки зацепления параллельно оси вала, и радиальная Fr силы(рис. 23, б): Ft=2T/d; Fr=Ft tg - угол наклона зубъев; - для косозубой цилиндрической передачи - окружная Ft, осевая Fa, направленная от точки зацепления параллельно оси вала, и радиальная Fr силы(рис. 23, б): Ft=2T/d; Fr=Ft tg 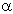 /cos /cos  ; Fa=Ft tg ; Fa=Ft tg  , где , где  - угол наклона зубъев; - для конической зубчатой передачи - окружная Ft, радиальная Fr и осевая Faсилы (рис. 23, в): Ft= 2T/d; Fr1=Fa2=Ft tg - угол наклона зубъев; - для конической зубчатой передачи - окружная Ft, радиальная Fr и осевая Faсилы (рис. 23, в): Ft= 2T/d; Fr1=Fa2=Ft tg 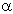 cos cos  1; Fr2=Fa1=Ft tg 1; Fr2=Fa1=Ft tg 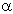 cos cos 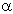 2, гдеd- средний делительный диаметр зубчатого колеса; 2, гдеd- средний делительный диаметр зубчатого колеса;  1, 1,  2- углы при начальныхконусах конической передачи. Для ортогональных передач ( 2- углы при начальныхконусах конической передачи. Для ортогональных передач (  1+ 1+  2=90°)tg 2=90°)tg  1=1/u=z1/z2; tg 1=1/u=z1/z2; tg  2= u = z2/ z1, где u- передаточное отношение передачи, z1, z2-числа зубъев колёс; - для червячных передач -окружная сила Ft, осевая Fa и радиальная Fr силы(рис.23 г): Ft1 =Fa2=2T1/d1, Ft 2=Fa1=2T2/d2, Fr1=Fr2= Ft 2 tg 2= u = z2/ z1, где u- передаточное отношение передачи, z1, z2-числа зубъев колёс; - для червячных передач -окружная сила Ft, осевая Fa и радиальная Fr силы(рис.23 г): Ft1 =Fa2=2T1/d1, Ft 2=Fa1=2T2/d2, Fr1=Fr2= Ft 2 tg 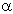 . В цепных и ремённых передачах нагрузки на валы определяются по приведённымранее формулам. Основным расчётом валов приводов является расчёт на прочность. Еговыполняют в три этапа. На первом этапе (предварительный расчёт) при отсутствии данных о размерахвала и изгибающих моментах, действующих в его сечениях, диаметр dвала приближённо определяется по известному крутящему моменту Т из условияпрочности по заниженным значениям допускаемых касательных напряжений[ . В цепных и ремённых передачах нагрузки на валы определяются по приведённымранее формулам. Основным расчётом валов приводов является расчёт на прочность. Еговыполняют в три этапа. На первом этапе (предварительный расчёт) при отсутствии данных о размерахвала и изгибающих моментах, действующих в его сечениях, диаметр dвала приближённо определяется по известному крутящему моменту Т из условияпрочности по заниженным значениям допускаемых касательных напряжений[  ]=12...20 МПа: ]=12...20 МПа:   Иногда на этом этапе расчёта диаметр хвостовика входного вала принимаютконструктивно, равным 0, 8...1, 0 диаметра вала приводного двигателя. На втором этапе разрабатывают конструкцию вала, обеспечивая условия сборкии технологичности изготовления. В результате определяют размеры всех участковвала и положения деталей на нём, что в совокупности с определёнными ранеенагрузками на вал позволяет построить его расчётную схему, необходимую дляреализации третьего этапа расчёта. Третий этап расчёта вала является проверочным, при котором производятоценку статической прочности и выносливости вала. Производят определениевнутренних силовых фактров в сечениях вала, который рассматривается при этомкак балка, шарнирно закреплённая на двух жёстких опорах. Такая модель вала иего закрепления близка к действительной для валов, вращающихся в опорах качения. При составлении расчётных схем валов следует обратить внимание нанаправление окружных сил зубчатых зацеплений. Так как только эта составляющаясилы взаимодействия колёс даёт крутящий момент относительно оси вала, тоориентироваться здесь надо на соблюдение условия равновесия равномерновращающегося вала и, следовательно, на равенство нулю суммы всех приложенных квалу крутящих моментов. Таким образом, если сопряжение колёс вала происходит сразных сторон от его оси, то направление окружных сил совпадает. В противном жеслучае направление сил Ft в зацеплениях различное. Оценку статической прочности производят посредством проверки выполненияусловия прочности, записываемого в виде Иногда на этом этапе расчёта диаметр хвостовика входного вала принимаютконструктивно, равным 0, 8...1, 0 диаметра вала приводного двигателя. На втором этапе разрабатывают конструкцию вала, обеспечивая условия сборкии технологичности изготовления. В результате определяют размеры всех участковвала и положения деталей на нём, что в совокупности с определёнными ранеенагрузками на вал позволяет построить его расчётную схему, необходимую дляреализации третьего этапа расчёта. Третий этап расчёта вала является проверочным, при котором производятоценку статической прочности и выносливости вала. Производят определениевнутренних силовых фактров в сечениях вала, который рассматривается при этомкак балка, шарнирно закреплённая на двух жёстких опорах. Такая модель вала иего закрепления близка к действительной для валов, вращающихся в опорах качения. При составлении расчётных схем валов следует обратить внимание нанаправление окружных сил зубчатых зацеплений. Так как только эта составляющаясилы взаимодействия колёс даёт крутящий момент относительно оси вала, тоориентироваться здесь надо на соблюдение условия равновесия равномерновращающегося вала и, следовательно, на равенство нулю суммы всех приложенных квалу крутящих моментов. Таким образом, если сопряжение колёс вала происходит сразных сторон от его оси, то направление окружных сил совпадает. В противном жеслучае направление сил Ft в зацеплениях различное. Оценку статической прочности производят посредством проверки выполненияусловия прочности, записываемого в виде  где где  -эквивалентный момент; МИ - изгибающий момент в опасномсечении вала, -эквивалентный момент; МИ - изгибающий момент в опасномсечении вала, 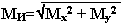 где Мх, Mу - составляющие изгибающего момента (см.рис.2), Мк-крутящий момент, Wx- осевой момент сопротивления сечения вала. Для определения значений моментовна основе полученных расчётных схем валов рекомендуется построить их эпюры, примеры которых рассмотрены в задачах 2 и 3 данного пособия. Сущность расчёта вала на выносливость состоит в определении коэффициентаn запаса прочности вала в опасных сечениях и сравнении его с допускаемымзначением [n]= 1, 5...2, 7. Опасными являются сечения вала, в которых действуютмаксимальные эквивалентные моменты Мэкв, сечения с различными концентратораминапряжений (шпоночными или шлицевыми канавками, галтелями, выточками, резьбами).Условие прочности имеет вид где Мх, Mу - составляющие изгибающего момента (см.рис.2), Мк-крутящий момент, Wx- осевой момент сопротивления сечения вала. Для определения значений моментовна основе полученных расчётных схем валов рекомендуется построить их эпюры, примеры которых рассмотрены в задачах 2 и 3 данного пособия. Сущность расчёта вала на выносливость состоит в определении коэффициентаn запаса прочности вала в опасных сечениях и сравнении его с допускаемымзначением [n]= 1, 5...2, 7. Опасными являются сечения вала, в которых действуютмаксимальные эквивалентные моменты Мэкв, сечения с различными концентратораминапряжений (шпоночными или шлицевыми канавками, галтелями, выточками, резьбами).Условие прочности имеет вид  где n где n 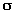 , n , n  - соответственно коэффициент запаса прочности по нормальным и покасательным напряжениям, - соответственно коэффициент запаса прочности по нормальным и покасательным напряжениям,  где где 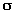 -1, -1,  -1-пределы выносливости материала вала по нормальным и касательнымнапряжениям, полученные при симметричных циклах нагружения на изгиб и кручение, определяются по данным справочников или расчётным путём (см. с. 10-11); -1-пределы выносливости материала вала по нормальным и касательнымнапряжениям, полученные при симметричных циклах нагружения на изгиб и кручение, определяются по данным справочников или расчётным путём (см. с. 10-11); 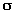 а, а,  а, а, 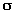 m, m,  m - амплитуда и средние напряжения циклов нормальных и касательныхнапряжений; k m - амплитуда и средние напряжения циклов нормальных и касательныхнапряжений; k 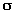 и k и k  - эффективные коэффициенты концентрации напряжений приизгибе и кручении; - эффективные коэффициенты концентрации напряжений приизгибе и кручении; 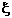 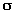 , , 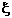  - коэффициенты, учитывающие снижение механическихсвойств материала с ростом размера заготовок; - коэффициенты, учитывающие снижение механическихсвойств материала с ростом размера заготовок;  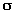 и и   - коэффициенты, учитывающиевлияние асимметрии цикла напряжений на выносливость материала. Значения всехэтих коэффициентов выбираются по таблицам справочников [1, 2, 3]. При расчёте валов механических передач принимается, что нормальныенапряжения, возникающие в основном из-за изгиба вала, изменяются по симметричномуциклу, для которого - коэффициенты, учитывающиевлияние асимметрии цикла напряжений на выносливость материала. Значения всехэтих коэффициентов выбираются по таблицам справочников [1, 2, 3]. При расчёте валов механических передач принимается, что нормальныенапряжения, возникающие в основном из-за изгиба вала, изменяются по симметричномуциклу, для которого  где Wx- осевой момент сопротивления сечения вала. Касательные напряжения где Wx- осевой момент сопротивления сечения вала. Касательные напряжения  , возникающие преимущественно под действием переменноговращающего момента, изменяются по отнулевому (пульсационному) циклу, для которого , возникающие преимущественно под действием переменноговращающего момента, изменяются по отнулевому (пульсационному) циклу, для которого  где Wp - полярный момент сопротивления сечения вала. Значения изгибающих и крутящих моментов в опасных сечениях вала определяютпо эпюрам изгибающих и крутящих моментов. Расчёт на жёсткость валов механизмов проводят как проверочный, который можетзаключаться либо в проверке прогибов и углов поворота сечений вала насоответствие их значений допускаемым (см. задачу 2), либо в проверке диаметрапо эквивалентной модели вала постоянного сечения: где Wp - полярный момент сопротивления сечения вала. Значения изгибающих и крутящих моментов в опасных сечениях вала определяютпо эпюрам изгибающих и крутящих моментов. Расчёт на жёсткость валов механизмов проводят как проверочный, который можетзаключаться либо в проверке прогибов и углов поворота сечений вала насоответствие их значений допускаемым (см. задачу 2), либо в проверке диаметрапо эквивалентной модели вала постоянного сечения:  где m- количество участков ступенчатого вала, i- номер участка вала длиной Liи диаметром di; L - общая длина вала. Условие жёсткости при этом ограничиваетугол закручивания v вала и имеет вид v < [v]. где m- количество участков ступенчатого вала, i- номер участка вала длиной Liи диаметром di; L - общая длина вала. Условие жёсткости при этом ограничиваетугол закручивания v вала и имеет вид v < [v]. 4. Подшипники качения Популярное:
|
Последнее изменение этой страницы: 2016-08-31; Просмотров: 1176; Нарушение авторского права страницы