Метод итерации по стратегиям без дисконтирования
При увеличении числа стационарных стратегий количество комбинаций может оказаться недопустимо большим.Поэтому использование метода полного перебора зачастую не оправдано, так как требует больших затрат машинного времени. Метод итераций по стратегиям лишен этого недостатка.
Метод итераций по стратегиям основывается на следующем. Для любой конкретной стратегии ожидаемый суммарный доход за n-ый этап определяется рекуррентным уравнением.
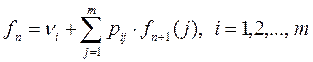
Это уравнение и служит основой метода итераций по стратегиям. Однако, чтобы сделать возможным изучение асимптотического поведения процесса, вид уравнения нужно немного изменить. В отличие от величины n, которая фигурирует в уравнении и соответствует i-му этапу, обозначим через η число оставшихся для анализа этапов. Тогда рекуррентное уравнение записывается в виде:
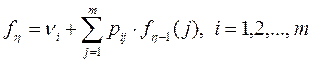
Здесь 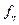 – суммарный ожидаемый доход при условии, что остались не рассмотренными η этапов. При таком определении η можно изучить асимптотическое поведение процесса, полагая при этом, что – суммарный ожидаемый доход при условии, что остались не рассмотренными η этапов. При таком определении η можно изучить асимптотическое поведение процесса, полагая при этом, что 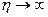 . .
Обозначим через 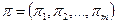 вектор установившихся вероятностей состояний с матрицей переходных вероятностей вектор установившихся вероятностей состояний с матрицей переходных вероятностей 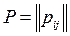 и пусть и пусть 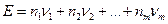 — ожидаемый доход за этап, тогда можно показать, что при достаточно большом η — ожидаемый доход за этап, тогда можно показать, что при достаточно большом η
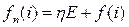 , ,
где 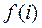 - постоянный член, описывающий асимптотическое поведение функции - постоянный член, описывающий асимптотическое поведение функции 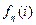 при заданном состоянии i. при заданном состоянии i.
Так как 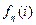 представляет суммарный оптимальный доход за η этапов при заданном состоянии i, а Е - ожидаемый доход за один этап, то интуитивно понятно, почему величина представляет суммарный оптимальный доход за η этапов при заданном состоянии i, а Е - ожидаемый доход за один этап, то интуитивно понятно, почему величина 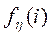 , равна сумме , равна сумме 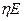 и поправочного числа и поправочного числа 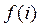 , учитывающего определенное состояние i. При этом, конечно, предполагается, что число η достаточно велико. Теперь рекуррентное уравнение можно записать в следующем виде. , учитывающего определенное состояние i. При этом, конечно, предполагается, что число η достаточно велико. Теперь рекуррентное уравнение можно записать в следующем виде.
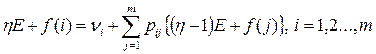
Упростив это уравнение, получаем:
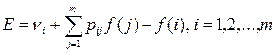 , ,
т.е. имеем m уравнений с 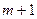 неизвестными неизвестными 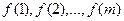 и E. и E.
Конечной целью является определение оптимальной стратегии, приводящей к максимальному значению Е. Так как имеется m уравнений с 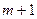 неизвестными, оптимальное значение Е нельзя определить за один шаг. В связи с этим используется итеративная процедура, начинающаяся с произвольной стратегии, а затем определяется новая стратегия, дающая лучшее значение Е. Итеративный процесс заканчивается, если две последовательно получаемые стратегии совпадают. неизвестными, оптимальное значение Е нельзя определить за один шаг. В связи с этим используется итеративная процедура, начинающаяся с произвольной стратегии, а затем определяется новая стратегия, дающая лучшее значение Е. Итеративный процесс заканчивается, если две последовательно получаемые стратегии совпадают.
Итеративный процесс состоит из двух основных шагов.
Шаг 1.Оценивание параметров.
Выбираем произвольную стратегию s. Используя соответствующие матрицы PS и RS произвольно полагая f(m) = 0, решаем уравнения
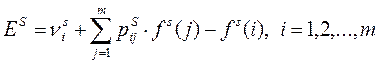 , ,
относительно неизвестных 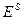 , ,  . .
Шаг 2.Улучшение стратегии.
Для каждого состояния определяем альтернативу k, обеспечивающую
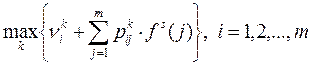
Здесь используются значения 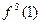 , j = 1, 2, …, m, определенные на шаге оценивания параметров. Результирующие оптимальные решения для состояний 1, 2, …, m формируют новую стратегию t. Если s и t идентичны, то алгоритм заканчивается; в этом случае t – оптимальная стратегия. В противном случае полагаем s = t и возвращаемся к шагу оценивания параметров. , j = 1, 2, …, m, определенные на шаге оценивания параметров. Результирующие оптимальные решения для состояний 1, 2, …, m формируют новую стратегию t. Если s и t идентичны, то алгоритм заканчивается; в этом случае t – оптимальная стратегия. В противном случае полагаем s = t и возвращаемся к шагу оценивания параметров.
Оптимизационная задача на шаге улучшения стратегии нуждается в пояснении. Целью этого шага является получение максимального значения Е. Как показано выше,
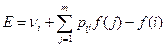
Поскольку f(i) не зависит от альтернативы k, задача максимизации на шаге улучшения стратегии эквивалентна максимизации Е по альтернативам k.
Пример решения задачи для конечного числа этапов
Формулировка задачи:
Мебельный магазин планирует свою работу на три месяца, при этом директору магазина необходимо решить: какие меры по стимулированию спроса, в зависимости от состояния дел, следует предпринять для увеличения объема продаж. Рассматриваются следующие варианты стимулирования спроса:
1. 3% скидка при следующей покупке;
2. бесплатная доставка;
3. не предпринимать ничего.
Кроме того, фирма оценивает месячный объем продаж по трехбалльной шкале как:
1. отличный;
2. хороший;
3. удовлетворительный.
Известны переходные вероятности и соответствующие месячные доходы по каждому из трех вариантов:
| 3% скидка при следующей покупке
|
| Бесплатная доставка
| | P1 =
|
|
|
|
|
| P2 =
|
|
|
|
| |
| 0, 4
| 0, 5
| 0, 1
|
|
| 0, 3
| 0, 6
| 0, 1
| |
| 0, 1
| 0, 6
| 0, 3
|
|
|
| 0, 4
| 0, 6
| |
|
| 0, 2
| 0, 8
|
|
|
| 0, 2
| 0, 8
| |
|
|
|
|
|
|
|
|
|
|
| | R1 =
|
|
|
|
|
| R2 =
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| | |
|
|
|
|
| |
|
|
|
| | Не предпринимать ничего
|
| |
|
|
|
| | P3 =
|
|
|
|
|
| |
|
|
|
| |
| 0, 3
| 0, 3
| 0, 4
|
| |
|
|
|
| |
| 0, 1
| 0, 7
| 0, 2
|
| |
|
|
|
| |
| 0, 05
| 0, 2
| 0, 75
|
| |
|
|
|
| |
|
|
|
|
|
| |
|
|
|
| | R3 =
|
|
|
|
|
| |
|
|
|
| |
|
|
|
|
| |
|
|
|
| |
|
|
|
|
| |
|
|
|
| |
|
|
|
|
| |
|
|
|
| Найти оптимальную стратегию стимуляции спроса для последующих 3 месяцев.
Решение:
В нашем случае число этапов – 3 (месяца), число состояний для каждого m = 3 (спрос отличный, хороший, удовлетворительный).
Вычислим значения  : :
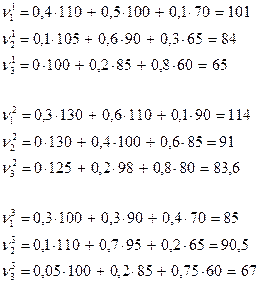
С учетом затрат на каждую стратегию (10, 20, 0):
| Этап 3:
| |
| 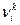
| Оптимальное решение
| | i
| k = 1
| k = 2
| k = 3
| 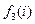
| 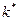
| |
|
|
|
|
|
| |
|
|
| 90, 5
|
|
| |
|
| 83, 6
|
| 83, 6
|
| |
| | Этап 2:
| |
| 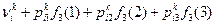
| Оптимальное решение
| | i
| k = 1
| k = 2
| k = 3
| 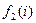
| 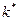
| |
| 101 + 0, 4·114 + 0, 5·91 + 0, 1·83, 6 = 200, 46
| 211, 16
| 179, 94
| 211, 16
|
| |
| 84 + 0, 1·114 + 0, 6·91 + 0, 3·83, 6 = 175, 08
| 177, 56
| 182, 32
| 182, 32
|
| |
| 65 + 0·114 + 0, 2·91+ 0, 8·83, 6 = 150, 8
| 168, 68
| 153, 6
| 168, 68
|
| | Этап 1:
| |
| 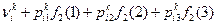
| Оптимальное решение
| | i
| k = 1
| k = 2
| k = 3
| 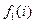
| 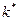
| |
| 101 + 0, 4·211, 16 + 0, 5·182, 32 + 0, 1·168, 68 = 293, 49
| 303, 61
| 270, 52
| 303, 61
|
| |
| 84 + 0, 1·211, 16 + 0, 6·182, 32 + 0, 3·168, 68 = 265, 11
| 265, 14
| 272, 98
| 272, 98
|
| |
| 65 + 0·211, 16 + 0, 2·
·182, 32 + 0, 8·168, 68 = 236, 41
| 255, 01
| 240, 53
| 255, 01
|
| Оптимальное решение показывает, что в 1-ый и 2-ой месяцы предприятию следует стимулировать спрос путем организации бесплатной доставки, при условии, что уровень спроса находится либо в отличном, либо в удовлетворительном состоянии. Если же уровень спроса хороший, то не следует ничего предпринимать. В 3-ем месяце магазину следует организовать бесплатную доставку мебели независимо от состояния системы.Суммарный ожидаемый доход за 3 месяца составит 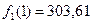 при отличном уровне продаж в 1-ый месяц, при отличном уровне продаж в 1-ый месяц, 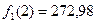 - при хорошем уровне и - при хорошем уровне и 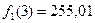 - при удовлетворительном уровне продаж в 1-ый месяц. - при удовлетворительном уровне продаж в 1-ый месяц.
Пример решения задачи с бесконечным числом этапов методом полного перебора
Формулировка задачи:
Мебельный магазин планирует свою работу на неопределенный период, при этом директору магазина необходимо решить: какие меры по стимулированию спроса, в зависимости от состояния дел, следует предпринять для увеличения объема продаж. Рассматриваются следующие варианты стимулирования спроса:
1. 3% скидка при следующей покупке;
2. Бесплатная доставка;
4. Не предпринимать ничего.
Кроме того, фирма оценивает месячный объем продаж по трехбалльной шкале как:
1. отличный;
2. хороший;
3. удовлетворительный.
В данной задаче принятия решений имеется 33 = 27 стационарных стратегий поведения, представленных в следующей таблице.
| s
| Действия
| |
| Не предпринимать никаких мер по стимулированию спроса.
| |
| Предложить 3% скидку при следующей покупке независимо от объема продаж.
| |
| Организовать бесплатную доставку независимо от объема продаж.
| |
| Предложить 3% скидку при следующей покупке, если объем продаж на уровне 1.
| |
| Предложить 3% скидку при следующей покупке, если объем продаж на уровне 2.
| |
| Предложить 3% скидку при следующей покупке, если объем продаж на уровне 3.
| |
| Предложить 3% скидку при следующей покупке, если объем продаж на уровне 1 или 2.
| |
| Предложить 3% скидку при следующей покупке, если объем продаж на уровне 1 или 3.
| |
| Предложить 3% скидку при следующей покупке, если объем продаж на уровне 2 или 3.
| |
| Организовать бесплатную доставку, если объем продаж на уровне 1.
| |
| Организовать бесплатную доставку, если объем продаж на уровне 2.
| |
| Организовать бесплатную доставку, если объем продаж на уровне 3.
| |
| Организовать бесплатную доставку, если объем продаж на уровне 1 или 2.
| |
| Организовать бесплатную доставку, если объем продаж на уровне 1 или 3.
| |
| Организовать бесплатную доставку, если объем продаж на уровне 2 или 3.
| |
| Предложить 3% скидку при следующей покупке, если объем продаж на уровне 1, и организовать бесплатную доставку, если объем продаж на уровне 2.
| |
| Предложить 3% скидку при следующей покупке, если объем продаж на уровне 1, и организовать бесплатную доставку, если объем продаж на уровне 3.
| |
| Предложить 3% скидку при следующей покупке, если объем продаж на уровне 2, и организовать бесплатную доставку, если объем продаж на уровне 3.
| |
| Предложить 3% скидку при следующей покупке, если объем продаж на уровне 2, и организовать бесплатную доставку, если объем продаж на уровне 1.
| |
| Предложить 3% скидку при следующей покупке, если объем продаж на уровне 3, и организовать бесплатную доставку, если объем продаж на уровне 1.
| |
| Предложить 3% скидку при следующей покупке, если объем продаж на уровне 3, и организовать бесплатную доставку, если объем продаж на уровне 2.
| |
| Предложить 3% скидку при следующей покупке, если объем продаж на уровне 1 или 2, и организовать бесплатную доставку, если объем продаж на уровне 3.
| |
| Предложить 3% скидку при следующей покупке, если объем продаж на уровне 1 или 3, и организовать бесплатную доставку, если объем продаж на уровне 2.
| |
| Предложить 3% скидку при следующей покупке, если объем продаж на уровне 1, и организовать бесплатную доставку, если объем продаж на уровне 2 или 3.
| |
| Предложить 3% скидку при следующей покупке, если объем продаж на уровне 2 или 3, и организовать бесплатную доставку, если объем продаж на уровне 1.
| |
| Предложить 3% скидку при следующей покупке, если объем продаж на уровне 2, и организовать бесплатную доставку, если объем продаж на уровне 1 или 3.
| |
| Предложить 3% скидку при следующей покупке, если объем продаж на уровне 3, и организовать бесплатную доставку, если объем продаж на уровне 1 или 2.
| Матрицы PS и RS:
| 1.
|
| | P1 =
|
|
|
|
|
| R1 =
|
|
|
|
| |
| 0, 3
| 0, 3
| 0, 4
|
|
|
|
|
| |
| 0, 1
| 0, 7
| 0, 2
|
|
|
|
|
| |
| 0, 05
| 0, 2
| 0, 75
|
|
|
|
|
| | 2.
| | P2 =
|
|
|
|
|
| R2 =
|
|
|
|
| |
| 0, 4
| 0, 5
| 0, 1
|
|
|
|
|
| |
| 0, 1
| 0, 6
| 0, 3
|
|
|
|
|
| |
|
| 0, 2
| 0, 8
|
|
|
|
|
| | 3.
| | P3 =
|
|
|
|
|
| R3 =
|
|
|
|
| |
| 0, 3
| 0, 6
| 0, 1
|
|
|
|
|
| |
|
| 0, 4
| 0, 6
|
|
|
|
|
| |
|
| 0, 2
| 0, 8
|
|
|
|
|
| | 4.
| | P4 =
|
|
|
|
|
| R4 =
|
|
|
|
| |
| 0, 4
| 0, 5
| 0, 1
|
|
|
|
|
| |
| 0, 1
| 0, 7
| 0, 2
|
|
|
|
|
| |
| 0, 05
| 0, 2
| 0, 75
|
|
|
|
|
| | 5.
| | P5 =
|
|
|
|
|
| R5 =
|
|
|
|
| |
| 0, 3
| 0, 3
| 0, 4
|
|
|
|
|
| |
| 0, 1
| 0, 6
| 0, 3
|
|
|
|
|
| |
| 0, 05
| 0, 2
| 0, 75
|
|
|
|
|
| | 6.
| | P6 =
|
|
|
|
|
| R6 =
|
|
|
|
| |
| 0, 3
| 0, 3
| 0, 4
|
|
|
|
|
| |
| 0, 1
| 0, 7
| 0, 2
|
|
|
|
|
| |
|
| 0, 2
| 0, 8
|
|
|
|
|
| | 7.
| | P7 =
|
|
|
|
|
| R7 =
|
|
|
|
| |
| 0, 4
| 0, 5
| 0, 1
|
|
|
|
|
| |
| 0, 1
| 0, 6
| 0, 3
|
|
|
|
|
| |
| 0, 05
| 0, 2
| 0, 75
|
|
|
|
|
| | 8.
| | P8 =
|
|
|
|
|
| R8 =
|
|
|
|
| |
| 0, 4
| 0, 5
| 0, 1
|
|
|
|
|
| |
| 0, 1
| 0, 7
| 0, 2
|
|
|
|
|
| |
|
| 0, 2
| 0, 8
|
|
|
|
|
| | 9.
|
| | P9 =
|
|
|
|
|
| R9 =
|
|
|
|
| |
| 0, 3
| 0, 3
| 0, 4
|
|
|
|
|
| |
| 0, 1
| 0, 6
| 0, 3
|
|
|
|
|
| |
|
| 0, 2
| 0, 8
|
|
|
|
|
| | 10.
| | P10 =
|
|
|
|
|
| R10 =
|
|
|
|
| |
| 0, 3
| 0, 6
| 0, 1
|
|
|
|
|
| |
| 0, 1
| 0, 7
| 0, 2
|
|
|
|
|
| |
| 0, 05
| 0, 2
| 0, 75
|
|
|
|
|
| | 11.
| | P11 =
|
|
|
|
|
| R11 =
|
|
|
|
| |
| 0, 3
| 0, 3
| 0, 4
|
|
|
|
|
| |
|
| 0, 4
| 0, 6
|
|
|
|
|
| |
| 0, 05
| 0, 2
| 0, 75
|
|
|
|
|
| | 12.
| | P12 =
|
|
|
|
|
| R12 =
|
|
|
|
| |
| 0, 3
| 0, 3
| 0, 4
|
|
|
|
|
| |
| 0, 1
| 0, 7
| 0, 2
|
|
|
|
|
| |
|
| 0, 2
| 0, 8
|
|
|
|
|
| | 13.
| | P13 =
|
|
|
|
|
| R13 =
|
|
|
|
| |
| 0, 3
| 0, 6
| 0, 1
|
|
|
|
|
| |
|
| 0, 4
| 0, 6
|
|
|
|
|
| |
| 0, 05
| 0, 2
| 0, 75
|
|
|
|
|
| | 14.
| | P14 =
|
|
|
|
|
| R14 =
|
|
|
|
| |
| 0, 3
| 0, 6
| 0, 1
|
|
|
|
|
| |
| 0, 1
| 0, 7
| 0, 2
|
|
|
|
|
| |
|
| 0, 2
| 0, 8
|
|
|
|
|
| | 15.
| | P15 =
|
|
|
|
|
| R15 =
|
|
|
|
| |
| 0, 3
| 0, 3
| 0, 4
|
|
|
|
|
| |
|
| 0, 4
| 0, 6
|
|
|
|
|
| |
|
| 0, 2
| 0, 8
|
|
|
|
|
| | 16.
| | P16 =
|
|
|
|
|
| R16 =
|
|
|
|
| |
| 0, 4
| 0, 5
| 0, 1
|
|
|
|
|
| |
|
| 0, 4
| 0, 6
|
|
|
|
|
| |
| 0, 05
| 0, 2
| 0, 75
|
|
|
|
|
| | 17.
|
| | P17 =
|
|
|
|
|
| R17 =
|
|
|
|
| |
| 0, 4
| 0, 5
| 0, 1
|
|
|
|
|
| |
| 0, 1
| 0, 7
| 0, 2
|
|
|
|
|
| |
|
| 0, 2
| 0, 8
|
|
|
|
|
| | 18.
| | P18 =
|
|
|
|
|
| R18 =
|
|
|
|
| |
| 0, 3
| 0, 3
| 0, 4
|
|
|
|
|
| |
| 0, 1
| 0, 6
| 0, 3
|
|
|
|
|
| |
| 0, 05
| 0, 2
| 0, 75
|
|
|
|
|
| | 19.
| | P19 =
|
|
|
|
|
| R19 =
|
|
|
|
| |
| 0, 3
| 0, 6
| 0, 1
|
|
|
|
|
| |
| 0, 1
| 0, 6
| 0, 3
|
|
|
|
|
| |
| 0, 05
| 0, 2
| 0, 75
|
|
|
|
|
| | 20.
| | P20 =
|
|
|
|
|
| R20 =
|
|
|
|
| |
| 0, 3
| 0, 6
| 0, 1
|
|
|
|
|
| |
| 0, 1
| 0, 7
| 0, 2
|
|
|
|
|
| |
|
| 0, 2
| 0, 8
|
|
|
|
|
| | 21.
| | P21 =
|
|
|
|
|
| R21 =
|
|
|
|
| |
| 0, 3
| 0, 3
| 0, 4
|
|
|
|
|
| |
|
| 0, 4
| 0, 6
|
|
|
|
|
| |
|
| 0, 2
| 0, 8
|
|
|
|
|
| | 22.
| | P22 =
|
|
|
|
|
| R22 =
|
|
|
|
| |
| 0, 4
| 0, 5
| 0, 1
|
|
|
|
|
| |
| 0, 1
| 0, 6
| 0, 3
|
|
|
|
|
| |
| 0, 05
| 0, 2
| 0, 75
|
|
|
|
|
| | 23.
| | P23 =
|
|
|
|
|
| R23 =
|
|
|
|
| |
| 0, 4
| 0, 5
| 0, 1
|
|
|
|
|
| |
|
| 0, 4
| 0, 6
|
|
|
|
|
| |
|
| 0, 2
| 0, 8
|
|
|
|
|
| | 24.
| | P24 =
|
|
|
|
|
| R24 =
|
|
|
|
| |
| 0, 4
| 0, 5
| 0, 1
|
|
|
|
|
| |
|
| 0, 4
| 0, 6
|
|
|
|
|
| |
|
| 0, 2
| 0, 8
|
|
|
|
|
| | 25.
|
| | P25 =
|
|
|
|
|
| R25 =
|
|
|
|
| |
| 0, 3
| 0, 6
| 0, 1
|
|
|
|
|
| |
| 0, 1
| 0, 6
| 0, 3
|
|
|
|
|
| |
|
| 0, 2
| 0, 8
|
|
|
|
|
| | 26.
| | P26 =
|
|
|
|
|
| R26 =
|
|
|
|
| |
| 0, 3
| 0, 6
| 0, 1
|
|
|
|
|
| |
| 0, 1
| 0, 6
| 0, 3
|
|
|
|
|
| |
|
| 0, 2
| 0, 8
|
|
|
|
|
| | 27.
| | P27 =
|
|
|
|
|
| R27 =
|
|
|
|
| |
| 0, 3
| 0, 6
| 0, 1
|
|
|
|
|
| |
|
| 0, 4
| 0, 6
|
|
|
|
|
| |
|
| 0, 2
| 0, 8
|
|
|
|
|
| | | | | | | | | | | | | | | | | | Результаты вычислений 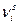 приведены в таблице. приведены в таблице.
| s
| i = 1
| i = 2
| i = 3
| |
|
| 90, 5
|
| |
|
|
|
| |
|
|
| 83, 6
| |
|
| 90, 5
|
| |
|
|
|
| |
|
| 90, 5
|
| |
|
|
|
| |
|
| 90, 5
|
| |
|
|
|
| |
|
| 90, 5
|
| |
|
|
|
| |
|
| 90, 5
| 83, 6
| |
|
|
|
| |
|
| 90, 5
| 83, 6
| |
|
|
| 83, 6
| |
|
|
|
| |
|
| 90, 5
| 83, 6
| |
|
|
|
| |
|
|
|
| |
|
| 90, 5
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
| 83, 6
| |
|
|
|
| |
|
|
| 83, 6
| |
|
|
|
|
Стационарные вероятности находятся из уравнений
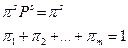
Для иллюстрации применения этих уравнений рассмотрим стратегию s = 1. Соответствующие уравнения имеют следующий вид.
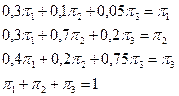
(Отметим, что одно из первых трех уравнений избыточно.) Решение системы будет
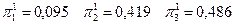 . .
В данном случае ожидаемый годовой доход равен
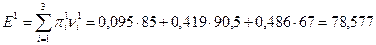 Результаты вычисления Результаты вычисления 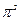 и и 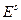 для всех стационарных стратегий приведены в следующей таблице. для всех стационарных стратегий приведены в следующей таблице.
| s
| 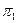
| 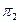
| 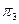
| 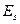
| |
| 0, 095
| 0, 419
| 0, 486
| 78, 557
| |
| 0, 061
| 0, 364
| 0, 575
| 74, 112
| |
|
| 0, 25
| 0, 75
| 85, 450
| |
| 0, 113
| 0, 468
| 0, 419
| 81, 840
| |
| 0, 049
| 0, 341
| 0, 61
| 73, 679
| |
| 0, 059
| 0, 412
| 0, 529
| 76, 686
| |
| 0, 107
| 0, 387
| 0, 506
| 77, 217
| |
| 0, 075
| 0, 444
| 0, 481
| 79, 022
| |
| 0, 049
| 0, 341
| 0, 61
| 72, 459
| |
| 0, 099
| 0, 479
| 0, 422
| 82, 910
| |
| 0, 05
| 0, 256
| 0, 694
| 74, 044
| |
| 0, 059
| 0, 412
| 0, 529
| 86, 525
| |
| 0, 048
| 0, 274
| 0, 678
| 75, 832
| |
| 0, 065
| 0, 452
| 0, 483
| 88, 695
| |
|
| 0, 25
| 0, 75
| 85, 450
| |
| 0, 056
| 0, 271
| 0, 673
| 75, 408
| |
| 0, 075
| 0, 444
| 0, 481
| 87, 969
| |
| 0, 09
| 0, 348
| 0, 562
| 74, 536
| |
| 0, 093
| 0, 395
| 0, 512
| 78, 086
| |
| 0, 065
| 0, 452
| 0, 483
| 79, 711
| |
|
| 0, 25
| 0, 75
| 71, 500
| |
| 0, 107
| 0, 387
| 0, 506
| 77, 217
| |
|
| 0, 25
| 0, 75
| 71, 500
| |
|
| 0, 25
| 0, 75
| 85, 450
| |
| 0, 053
| 0, 368
| 0, 579
| 74, 589
| |
| 0, 053
| 0, 368
| 0, 579
| 85, 358
| |
|
| 0, 25
| 0, 75
| 71, 500
| Вывод: Из таблицы видно, что стратегия 14 (организовать бесплатную доставку, если объем продаж на уровне 1 или 3) дает наибольший ожидаемый месячный доход. Следовательно, это и есть оптимальная долгосрочная стратегия.
Пример решения задачи с бесконечным числом этапов методом итерации по стратегиям без дисконтирования
Решим задачу, описанную в предыдущем примере методом итерации по стратегиям без дисконтирования.
Решение задачи можно начать с произвольной стратегии. Пусть в качестве начальной рассматривается стратегия, исключающая применение каких-либо мер по стимулированию спроса. Имеем соответствующие матрицы.
| P1 =
|
|
|
|
|
| R1 =
|
|
|
|
| |
| 0, 3
| 0, 3
| 0, 4
|
|
|
|
|
| |
| 0, 1
| 0, 7
| 0, 2
|
|
|
|
|
| |
| 0, 05
| 0, 2
| 0, 75
|
|
|
|
|
| Уравнения шага оценивания параметров принимают вид
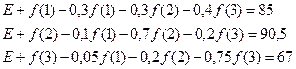
Полагая f(3) = 0, получаем решение этих уравнений
E = 78, 547, f(1) = 30, 676, f(2) = 50, 068, f(3) = 0.
Перейдем к шагу улучшения стратегии. Результаты вычислений приведены в таблице.
|
| 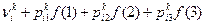
| Оптимальное решение
| | i
| k = 1
| k = 2
| k = 3
| f(i)
| 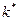
| |
| 85 + 0, 3·30, 676 + 0, 3·50, 068 + 0, 4·0= 109, 223
| 138, 304
| 153, 244
| 153, 244
|
| |
| 90, 5 + 0, 1·30, 676 + 0, 7·50, 068 + 0, 2·0= 128, 615
| 117, 108
| 111, 027
| 128, 615
|
| |
| 67 + 0, 05·30, 676 + 0, 2·50, 068 + 0, 75·0= 78, 547
| 75, 014
| 93, 614
| 93, 614
|
| Новая стратегия предусматривает организацию бесплатной доставки, если объем продаж на уровне 1 или 3. Новой стратегии соответствуют матрицы
| P14 =
|
|
|
|
|
| R14 =
|
|
|
|
| |
| 0, 3
| 0, 6
| 0, 1
|
|
|
|
|
| |
| 0, 1
| 0, 7
| 0, 2
|
|
|
|
|
| |
|
| 0, 2
| 0, 8
|
|
|
|
|
| Эти матрицы определяют следующие уравнения:
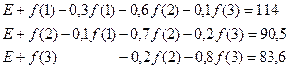
Полагая f(3) = 0, получаем решение этих уравнений
E = 88, 677, f(1) = 57, 935, f(2) = 25, 387, f(3) = 0.
Результаты вычислений на шаге улучшения стратегии приведены в следующей таблице.
|
| 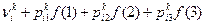
| Оптимальное решение
| | i
| k = 1
| k = 2
| k = 3
| f(i)
| 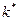
| |
| 109, 997
| 136, 868
| 146, 613
| 146, 613
|
| |
| 114, 064
| 105, 026
| 101, 155
| 114, 064
|
| |
| 74, 974
| 70, 077
| 88, 677
| 88, 677
|
| Новая стратегия идентична предыдущей, поэтому последняя стратегия оптимальна и итеративный процесс заканчивается. Естественно, что этот результат совпадает с результатом, полученным методом полного перебора. Однако, следует отметить, что метод итерации по стратегиям достаточно быстро сходится к оптимальному решению, что является его характерной особенностью.
Заключение
В настоящем методическом указании рассмотрены три алгоритма принятия решения: в условиях определенности, в условиях риска и в условиях неопределенности.
В первой части указания изложена методика принятия ре
Популярное:
|

