Взаимное расположение прямых на плоскости. Расстояние от точки до прямой
Пример. Даны прямые 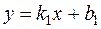 и
и 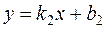 . Требуется найти угол
. Требуется найти угол  между ними.
между ними.
►

.
Обозначения и их смысл смотри на рисунке.
Следствие 1 (условие совпадения прямых). Две прямые  и
и  совпадают тогда и только тогда, когда
совпадают тогда и только тогда, когда 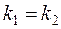 и
и  .
.
Следствие 2 (условие параллельности прямых). Две прямые  и
и  параллельны тогда и только тогда, когда
параллельны тогда и только тогда, когда 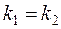 и
и 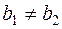 .
.
Следствие 3 (условие перпендикулярности прямых). Две прямые  и
и  перпендикулярны тогда и только тогда, когда
перпендикулярны тогда и только тогда, когда  .
.
Действительно, прямые перпендикулярны 
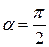

 не существует
не существует 


 . ◄
. ◄
Пусть прямые  и
и  заданы общими уравнениями
заданы общими уравнениями
Заметим, что если две прямые заданы своими общими уравнениями  и
и  , то могут представиться три случая:
, то могут представиться три случая:
1) 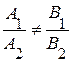 – прямые имеют одну общую точку;
– прямые имеют одну общую точку;
2)  – прямые параллельны;
– прямые параллельны;
3)  – прямые совпадают.
– прямые совпадают.
Пример. Найти точку равновесия, если функции спроса и предложения заданы следующими соотношениями:  и
и 
► Из условия равновесия спроса и предложения  получаем
получаем 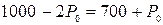 , откуда следует
, откуда следует  , и, таким образом, цена равновесия составляет
, и, таким образом, цена равновесия составляет 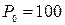 . На плоскости
. На плоскости  графики функций спроса
графики функций спроса  и предложения
и предложения  – прямые; цена равновесия – абсцисса точки пересечения графиков функций спроса и предложения. ◄
– прямые; цена равновесия – абсцисса точки пересечения графиков функций спроса и предложения. ◄
Типовой пример ( расстояние от точки до прямой на плоскости).
Если задана точка  , то расстояние до прямой
, то расстояние до прямой  определяется как
определяется как
 .
.
► Пусть точка 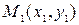 – основание перпендикуляра, опущенного из точки
– основание перпендикуляра, опущенного из точки 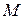 на заданную прямую. Тогда расстояние между точками
на заданную прямую. Тогда расстояние между точками 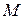 и
и  :
:
 (1)
(1)
Координаты  и
и  могут быть найдены как решение системы уравнений:
могут быть найдены как решение системы уравнений:

Второе уравнение системы – это уравнение прямой, проходящей через заданную точку  перпендикулярно заданной прямой.
перпендикулярно заданной прямой.
Если преобразовать первое уравнение системы к виду:

 то, решая, получим:
то, решая, получим:
 .
.
Подставляя эти выражения в уравнение (1), находим:
 .◄
.◄
Расстояние от точки до прямой на плоскости (второй способ)







Пусть дана прямая  :
:  , где
, где  – ее нормальный вектор, и пусть точка
– ее нормальный вектор, и пусть точка 

 , т. е.
, т. е.  . Требуется определить расстояние от точки
. Требуется определить расстояние от точки  до прямой
до прямой  .
.
Пусть  — ортогональная проекция точки
— ортогональная проекция точки  на прямую
на прямую  . Тогда
. Тогда



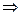

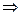
 .
.
Очевидно,  = {
= { 
 ,
, 
 }. Отсюда
}. Отсюда



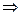


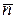 или
или 

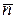 .
.
Напомним, что (  ,
, 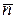 ) =
) = 


 , где
, где  — угол между векторами
— угол между векторами  и
и 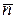 ; здесь
; здесь

 =
= 
Отсюда
(  ,
, 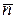 ) =
) = 
 и |(
и |(  ,
, 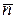 )| =
)| = 
 .
.
Следовательно,
 =
=  =
=  =
=
 =
=  .
.
Таким образом, расстояние  от точки
от точки  до прямой
до прямой  находится по формуле
находится по формуле
 =
=  =
=  .
.
Найдем теперь расстояние от начала координат  до прямой
до прямой  :
:
 =
=  .
.
Типовой пример. Найти расстояние от точки  до прямой
до прямой  .
.
► Расстояние  от точки до прямой равно:
от точки до прямой равно:
 .◄
.◄
Типовой пример. Даны вершины треугольника 
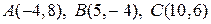 . Найти: 1) длину стороны
. Найти: 1) длину стороны 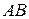 ; 2) уравнение высоты
; 2) уравнение высоты 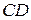 и ее длину; 3) уравнение медианы, проведенной из вершины
и ее длину; 3) уравнение медианы, проведенной из вершины  ; 4) написать уравнение прямой, проходящей через точку
; 4) написать уравнение прямой, проходящей через точку 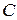 параллельно стороне
параллельно стороне 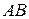 .
.
► 1) Расстояние  между точками
между точками 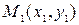 и
и  определяется по формуле
определяется по формуле
 . (1)
. (1)
Подставим в формулу (1) координаты точек А и В, получим
 .
.
2) Уравнение прямой, проходящей через точки 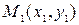 и
и  , имеет вид
, имеет вид
 (2)
(2)
Подставив в формулу (2) координаты точек  и
и  , получим уравнение прямой
, получим уравнение прямой 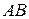 :
:

Для нахождения углового коэффициента  прямой
прямой 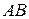 разрешим полученное уравнение относительно
разрешим полученное уравнение относительно  :
:  .
.
Отсюда  . Т.к. высота
. Т.к. высота 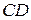 перпендикулярна
перпендикулярна 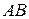 , то угловой коэффициент
, то угловой коэффициент 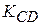 будет равен
будет равен  ,
, 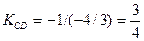 .
.
Искомая высота проходит через точку  . Воспользуемся уравнением прямой, проходящей через данную точку, с заданным угловым коэффициентом:
. Воспользуемся уравнением прямой, проходящей через данную точку, с заданным угловым коэффициентом:
 . (3)
. (3)
Имеем  (
( 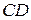 )
)
Для нахождения длины 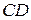 определим координаты точки
определим координаты точки 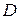 , решив систему уравнений (
, решив систему уравнений ( 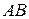 ) и (
) и ( 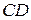 ):
):
 ,
,
откуда  , т.е.
, т.е.  .
.
Подставив в формулу (1) координаты точек 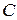 и
и 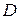 , находим
, находим

3) Обозначим основание искомой медианы через 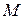 . По определению, медиана
. По определению, медиана 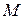 делит сторону
делит сторону  пополам. Координаты точки
пополам. Координаты точки 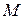 найдем по формуле
найдем по формуле
 (4)
(4)

Чтобы записать уравнение медианы  , воспользуемся формулой (2):
, воспользуемся формулой (2):  ,
, 
 ,
, 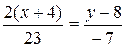 ,
,  (
(  )
)
4) Обозначим искомую прямую  . Угловой коэффициент
. Угловой коэффициент  , т.к.
, т.к. 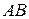 и
и  параллельны, то
параллельны, то 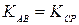 искомая прямая проходит через точку
искомая прямая проходит через точку  . Воспользуемся уравнением (3):
. Воспользуемся уравнением (3):
 ,
,  ,
,  (
(  ) ◄
) ◄
Типовой пример. Даны вершины треугольника  ,
,  ,
,  . Найти точку пересечения высоты
. Найти точку пересечения высоты  , опущенной из вершины
, опущенной из вершины  , и медианы
, и медианы  , проведенной из вершины
, проведенной из вершины  , а также острый угол, заключенный между ними
, а также острый угол, заключенный между ними
► Используя уравнение прямой, проходящей через две заданные точки, найдем сначала уравнение стороны 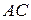 треугольника
треугольника  . Получим:
. Получим:
 или
или 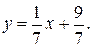



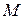


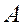

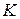
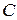
Угловой коэффициент этой прямой равен  . Так как высота
. Так как высота 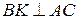 , ее угловой коэффициент можно найти по формуле
, ее угловой коэффициент можно найти по формуле  . Поскольку нам известна точка
. Поскольку нам известна точка  , то уравнение высоты
, то уравнение высоты  находим так:
находим так: 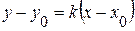 . Получаем:
. Получаем: 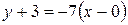 или
или  .
.
Найдем теперь уравнение медианы  . Координаты точки
. Координаты точки 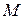 (середины отрезка
(середины отрезка  ) находим по формулам:
) находим по формулам:
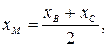
 . Имеем:
. Имеем: 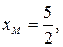
 . Используя уравнение прямой, проходящей через две заданные точки, получим уравнение медианы
. Используя уравнение прямой, проходящей через две заданные точки, получим уравнение медианы  :
:
 или
или 
Координаты точки  пересечения высоты
пересечения высоты  и медианы
и медианы  находим теперь как решение системы уравнений
находим теперь как решение системы уравнений
 Имеем:
Имеем: 
 . Наконец, используя формулу
. Наконец, используя формулу 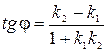 , находим острый угол
, находим острый угол  между
между  и
и 
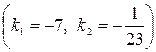 :
:
 ◄
◄
Пример. Определить линейную зависимость  между полными издержками производства предприятия, изготавливающего однородную продукцию, и объемом производства, если:
между полными издержками производства предприятия, изготавливающего однородную продукцию, и объемом производства, если:
постоянные издержки (например, затраты на содержание административных зданий, их отопление и т.д.), не зависящие от объема продукции, составляют  (денежных единиц);
(денежных единиц);
переменные издержки (например, материальные затраты) пропорциональны с коэффициентом  объему
объему  изготавливаемой продукции. Записать эту функцию для
изготавливаемой продукции. Записать эту функцию для  (млн.руб.) и
(млн.руб.) и  (млн.руб. на одну единицу продукции).
(млн.руб. на одну единицу продукции).
► В данном случае между полными издержками  некоторого производства и количеством
некоторого производства и количеством  произведенной продукции имеет место линейная зависимость вида:
произведенной продукции имеет место линейная зависимость вида:  , где
, где  – удельные переменные издержки (издержки на одну условную единицу продукции), а
– удельные переменные издержки (издержки на одну условную единицу продукции), а  – постоянные издержки производства. В случае
– постоянные издержки производства. В случае  (млн. руб.) и
(млн. руб.) и  (млн. на одну условную единицу продукции) имеем уравнение
(млн. на одну условную единицу продукции) имеем уравнение 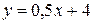 .◄
.◄
Пример. Весь объем основных фондов предприятия в 1991 году вырос на 6% по сравнению с объемом 1990 года. Начиная с 1992 года, в течение последующих пяти лет прирост основных фондов составлял 7% ежегодно. Записать формулу роста основных фондов в течение пятилетки.
► Пусть  – время в годах,
– время в годах,  – соответствующий объем основных фондов в процентах. Значение объема основных фондов
– соответствующий объем основных фондов в процентах. Значение объема основных фондов  = 106% соответствует моменту
= 106% соответствует моменту  = 1 (1991-му – первому году пятилетки). Ежегодный прирост составляет 7%. К моменту времени
= 1 (1991-му – первому году пятилетки). Ежегодный прирост составляет 7%. К моменту времени  этот прирост будет равен
этот прирост будет равен  , а с другой стороны эта величина равна разности
, а с другой стороны эта величина равна разности  . Следовательно, имеем формулу:
. Следовательно, имеем формулу:  или
или  . Здесь
. Здесь  принимает значения: 1, 2, 3, 4, 5. График функции
принимает значения: 1, 2, 3, 4, 5. График функции  на отрезке [1, 5] изображен на рис.◄
на отрезке [1, 5] изображен на рис.◄
 у
у



 134
134

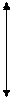

y - 106


 106
106
 x
x
0 1 2 3 4 5

1991 1992 1993 1994 1995 x
Пример. Полные издержки по производству 5 условных единиц продукции составляют 5, 5 млн. рублей, а по производству 10 усл. ед. – 9 млн. рублей. Найти функцию издержек производства, считая ее линейной. Определить издержки по производству 7 условных единиц продукции.
► По условию задачи можно считать, что даны две точки (5; 5, 5) и (10; 9) искомой прямой. Используя заданное уравнение, получим:  , или
, или  , или
, или  . Следовательно, искомая линейная функция издержек имеет вид:
. Следовательно, искомая линейная функция издержек имеет вид:  . Подставив в найденную формулу
. Подставив в найденную формулу  значение
значение  , подсчитаем издержки:
, подсчитаем издержки:  (млн. руб.) по производству 7 условных единиц продукции.◄
(млн. руб.) по производству 7 условных единиц продукции.◄
Пример. Полные издержки по производству х единиц продукции на двух предприятиях (см. примеры 1 и 3) выражаются соответственно формулами:  :
:  и
и  :
: 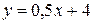 , где
, где  (усл. ед.) – объем продукции, а
(усл. ед.) – объем продукции, а  (млн. руб.) – соответствующие полные издержки. Требуется выяснить, начиная с какого объема продукции более экономичным становится второе предприятие.
(млн. руб.) – соответствующие полные издержки. Требуется выяснить, начиная с какого объема продукции более экономичным становится второе предприятие.
► Построим прямые  и
и  .
.

 l1
l1
 у A l2
у A l2

 9
9

0 1 2 3 4 5 6 7 8 9 10 х
Найдем координаты точки их пересечения, решив следующую систему уравнений:

Следовательно, точка  пересечения прямых имеет координаты
пересечения прямых имеет координаты 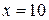 и
и  . Это значит, что при объеме продукции
. Это значит, что при объеме продукции 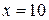 усл. ед. полные издержки по производству этого объема на обоих предприятиях одинаковы и составляют 9 млн. руб.
усл. ед. полные издержки по производству этого объема на обоих предприятиях одинаковы и составляют 9 млн. руб.
Из чертежа видно, что при объеме  усл. ед. более экономичным (издержки меньше) становится второе предприятие. Это можно установить и без помощи графика (аналитически). Действительно, если обозначить
усл. ед. более экономичным (издержки меньше) становится второе предприятие. Это можно установить и без помощи графика (аналитически). Действительно, если обозначить  и
и  , то
, то  Û
Û  Û
Û  Û
Û  .◄
.◄
Пример. Между пунктами  и
и  проложен прямолинейно провод телефонной связи. Необходимо подключить к этому проводу пункт
проложен прямолинейно провод телефонной связи. Необходимо подключить к этому проводу пункт  по кратчайшему расстоянию. Найти точку подключения
по кратчайшему расстоянию. Найти точку подключения  и длину необходимого для этого провода. На плане местности размеры даны в километрах.
и длину необходимого для этого провода. На плане местности размеры даны в километрах.
► Кратчайшим расстоянием от пункта  до прямой
до прямой  является длина перпендикуляра
является длина перпендикуляра  , опущенного на
, опущенного на  из точки
из точки 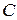 . Следовательно, необходимо найти уравнение прямой
. Следовательно, необходимо найти уравнение прямой  , перпендикулярной
, перпендикулярной  и установить длину искомого отрезка.
и установить длину искомого отрезка.
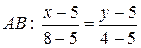
 .
.
Так как угловой коэффициент прямой 
 , то угловой коэффициент прямой
, то угловой коэффициент прямой 
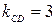 . Имеем
. Имеем  .
.
Найдем координаты точки  :
:

2) обозначим через  расстояние от точки
расстояние от точки 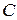 до прямой
до прямой  , тогда:
, тогда:  (км). Следовательно, точка подключения к телефонному проводу будет иметь координаты (3, 5; 5, 5) на плане местности, а длина требующегося провода составит 4, 7 км. ◄
(км). Следовательно, точка подключения к телефонному проводу будет иметь координаты (3, 5; 5, 5) на плане местности, а длина требующегося провода составит 4, 7 км. ◄
Плоскость
1. Общее уравнение плоскости. Пусть заданы: система координат  , плоскость
, плоскость  , точка
, точка  и вектор
и вектор 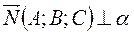 . Произвольная точка
. Произвольная точка  принадлежит плоскости
принадлежит плоскости  тогда и только тогда, когда векторы
тогда и только тогда, когда векторы  и
и  будут перпендикулярны, т.е.
будут перпендикулярны, т.е. 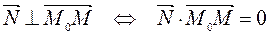 . Координаты векторов:
. Координаты векторов:  ,
, 
 . Следовательно,
. Следовательно,
 (1) – уравнение плоскости, проходящей через данную точку, перпендикулярной данному вектору, где
(1) – уравнение плоскости, проходящей через данную точку, перпендикулярной данному вектору, где 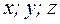 – текущие координаты;
– текущие координаты;  - координаты точки
- координаты точки 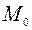 ;
; 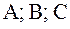 – координаты вектора
– координаты вектора  . Преобразуем уравнение (1).
. Преобразуем уравнение (1).
 . Получим
. Получим  (2) – общее уравнение плоскости
(2) – общее уравнение плоскости  .
.
Из общего уравнения получаем вектор  , называемый нормальным вектором плоскости
, называемый нормальным вектором плоскости  .
.
Типовой пример. Составить уравнение плоскости, проходящей через точку 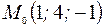 перпендикулярной вектору
перпендикулярной вектору  .
.
► Применяя уравнение (1), получим:  ;
;
 или
или 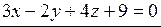 – это и есть общее уравнение плоскости. ◄
– это и есть общее уравнение плоскости. ◄
Популярное:


 .
.