Линии второго порядка на плоскости
1.Эллипс.Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек  и
и  , называемых фокусами, есть величина постоянная
, называемых фокусами, есть величина постоянная  , большая, чем расстояние между фокусами
, большая, чем расстояние между фокусами 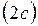 .
.
Каноническое уравнение эллипса имеет вид:
 , где
, где  .
.
Расположим систему координат следующим образом: за ось 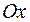 примем прямую, проходящую через фокусы
примем прямую, проходящую через фокусы  и
и  , за ось
, за ось 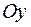 примем перпендикуляр к оси абсцисс, проходящий через середину отрезка
примем перпендикуляр к оси абсцисс, проходящий через середину отрезка 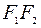 .
.  ,
,  ,
,  и
и 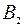 - точки пересечения эллипса с осями симметрии (координатными осями) называются вершинами эллипса. Отрезки
- точки пересечения эллипса с осями симметрии (координатными осями) называются вершинами эллипса. Отрезки 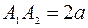 и
и 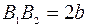 называются осями эллипса, причем
называются осями эллипса, причем 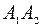 – большая ось, а
– большая ось, а  - малая ось, так как
- малая ось, так как 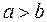 . Параметры
. Параметры  и
и  , входящие в канониче
, входящие в канониче 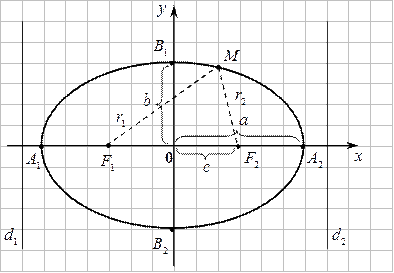 ское уравнение, называются полуосями эллипса, а
ское уравнение, называются полуосями эллипса, а 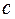 называется фокусным расстоянием эллипса. Эксцентриситетом эллипса называется отношение фокусного расстояния к большей полуоси
называется фокусным расстоянием эллипса. Эксцентриситетом эллипса называется отношение фокусного расстояния к большей полуоси  . Очевидно, что
. Очевидно, что 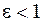 . Прямые
. Прямые 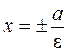 называются директрисами эллипса
называются директрисами эллипса 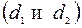 .
.
Пусть точка 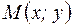 – произвольная точка эллипса. Длины отрезков
– произвольная точка эллипса. Длины отрезков  и
и 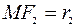 называются фокальными радиусами
называются фокальными радиусами 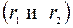 .
.
 и
и 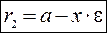
 Если фокусы эллипса лежат на оси
Если фокусы эллипса лежат на оси 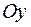 , то большей осью будет отрезок
, то большей осью будет отрезок 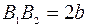 , а малой осью отрезок
, а малой осью отрезок 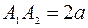 . Тогда
. Тогда  , а директрисами
, а директрисами 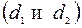 являются прямые
являются прямые  . Если
. Если  , то эллипс превращается в окружность, определяемую уравнением
, то эллипс превращается в окружность, определяемую уравнением
 .
.
Уравнение  определяет вырожденный эллипс, т.е. это уравнение определяет на плоскости
определяет вырожденный эллипс, т.е. это уравнение определяет на плоскости 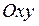 только одну точку
только одну точку 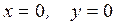 . Уравнение
. Уравнение 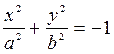 определяет мнимый эллипс, т.е. это уравнение не определяет на плоскости
определяет мнимый эллипс, т.е. это уравнение не определяет на плоскости 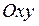 никакого геометрического образа.
никакого геометрического образа.
Если центр эллипса находится в точке  и оси параллельны осям координат, то его уравнение имеет вид:
и оси параллельны осям координат, то его уравнение имеет вид:
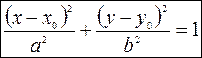
Типовой пример. Построить кривую 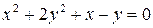 .
.
► Выделяем полные квадраты.
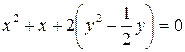 ,
, 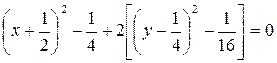 ,
,
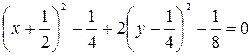 ,
, 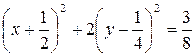 ,
,
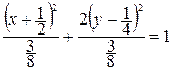 ,
,  .
.
Это эллипс. 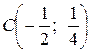 ;
;  ,
, 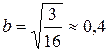 .◄
.◄
2. Гипербола.Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек  и
и  , называемых фокусами гиперболы, есть величина постоянная
, называемых фокусами гиперболы, есть величина постоянная  , меньшая, чем расстояние между фокусами
, меньшая, чем расстояние между фокусами 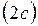 .
.
Каноническое уравнение гиперболы имеет вид 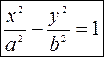 , где
, где 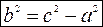 .
.
Расположим систему координат следующим образом: за ось 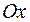 примем прямую, проходящую через фокусы
примем прямую, проходящую через фокусы  и
и  , за ось
, за ось 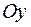 примем перпендикуляр к оси абсцисс, проходящий через середину отрезка
примем перпендикуляр к оси абсцисс, проходящий через середину отрезка 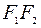 .
.
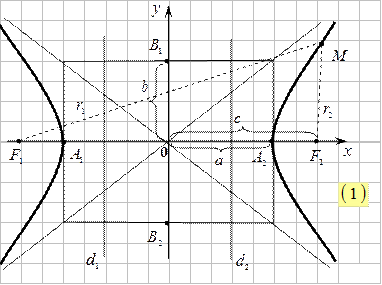
Гипербола имеет две оси симметрии (оси координат), с одной из которых она пересекается в точках  ,
,  , называемых вершинами гиперболы. Отрезок
, называемых вершинами гиперболы. Отрезок 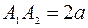 – действительная ось,
– действительная ось, 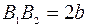 – мнимая ось. Параметры
– мнимая ось. Параметры  и
и  , входящие в каноническое уравнение, называются полуосями гиперболы, а
, входящие в каноническое уравнение, называются полуосями гиперболы, а 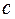 называется фокусным расстоянием гиперболы. Прямоугольник со сторонами
называется фокусным расстоянием гиперболы. Прямоугольник со сторонами 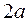 и
и 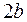 называется основным прямоугольником гиперболы. Диагонали этого прямоугольника называются асимптотами гиперболы. Уравнения асимптот имеют вид:
называется основным прямоугольником гиперболы. Диагонали этого прямоугольника называются асимптотами гиперболы. Уравнения асимптот имеют вид:
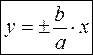
Эксцентриситетом гиперболы называется отношение фокусного расстояния к длине действительной полуоси  . Очевидно, что
. Очевидно, что 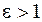 . Прямые
. Прямые 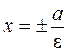 называются директрисами гиперболы
называются директрисами гиперболы 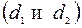 .
.
Пусть точка 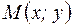 – произвольная точка гиперболы.
– произвольная точка гиперболы.
Длины отрезков  и
и 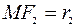 называются фокальными радиусами
называются фокальными радиусами 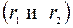 .
. 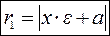 и
и 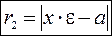
Если гипербола расположена так, что ее фокусы лежат на оси 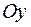 , то действительной осью будет отрезок
, то действительной осью будет отрезок 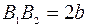 , а мнимой осью – отрезок
, а мнимой осью – отрезок 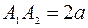 и уравнение ее имеет вид
и уравнение ее имеет вид 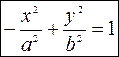 .
. 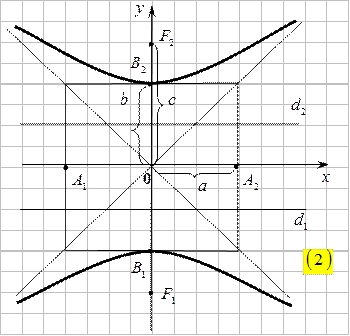 Тогда
Тогда  и директрисами
и директрисами 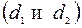 являются прямые
являются прямые 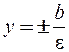 , а асимптоты будут те же, что и у гиперболы (1).
, а асимптоты будут те же, что и у гиперболы (1).
Гиперболы(1)и(2)называются сопряженными.Если  , то гипербола называется равносторонней.
, то гипербола называется равносторонней.
Простейшие уравнения равносторонней гиперболы имеют вид:
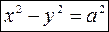 ,
,  .
.
Если центр гиперболы находится в точке  и оси параллельны осям координат, то уравнение ее имеет вид:
и оси параллельны осям координат, то уравнение ее имеет вид:
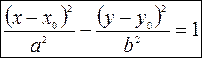 или
или  .
.
3. Парабола.Параболой называется множество всех точек плоскости, каждая из которых одинаково удалена от данной точки 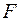 , называемой фокусом, и данной прямой
, называемой фокусом, и данной прямой 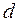 , называемой директрисой.
, называемой директрисой.
Величина 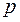 , равная расстоянию от фокуса до директрисы, называется параметром параболы.
, равная расстоянию от фокуса до директрисы, называется параметром параболы.
Расположим систему координат следующим образом: за одну из координатных осей примем ось параболы, а за другую – прямую, перпендикулярную оси и проведенную посередине между фокусом и директрисой.
Тогда уравнения параболы будут иметь вид:
Пусть вершина параболы находится в точке 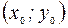 , тогда ее уравнения имеют вид: если ось параболы параллельна оси
, тогда ее уравнения имеют вид: если ось параболы параллельна оси 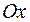 , то
, то 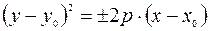 ; если ось параболы параллельна оси
; если ось параболы параллельна оси 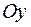 , то
, то 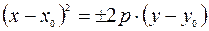 .
.
 Типовой пример.Построить параболу
Типовой пример.Построить параболу 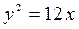 . Записать координаты фокуса и уравнения директрисы.
. Записать координаты фокуса и уравнения директрисы.
► Из канонического уравнения параболы определим: 1) 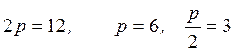 .
.
2) Ось параболы - 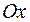 , вершина – точка
, вершина – точка  , фокус –
, фокус –  , директриса – прямая
, директриса – прямая 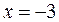 .
.
3) Из определения параболы следует, что параболе принадлежат точки, которые лежат на прямой, параллельной директрисе, на расстоянии  от фокуса. ◄
от фокуса. ◄
4. Общее уравнение линии второго порядка.Общее уравнение имеет вид
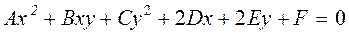 .
.
Коэффициенты 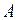 ,
, 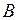 и
и 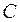 одновременно в нуль не обращаются. С помощью преобразования системы координат общее уравнение линии второго порядка может быть приведено к каноническому виду.
одновременно в нуль не обращаются. С помощью преобразования системы координат общее уравнение линии второго порядка может быть приведено к каноническому виду.
Пусть 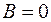 . Получим общее уравнение линии второго порядка с осями симметрии, параллельными осям координат.
. Получим общее уравнение линии второго порядка с осями симметрии, параллельными осям координат.

Оно приводится к каноническому виду с помощью параллельного переноса осей координат. При приведении общего уравнения к каноническому виду удобно использовать метод выделения полных квадратов.
По коэффициентам уравнения можно определить вид кривой:
если  , то это уравнение окружности;
, то это уравнение окружности;
если 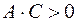 , то это уравнение эллипса;
, то это уравнение эллипса;
если 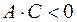 , то это уравнение гиперболы;
, то это уравнение гиперболы;
если 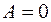 или
или 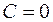 , то это уравнение параболы.
, то это уравнение параболы.
Типовые примеры.
1) Привести общее уравнение  к каноническому виду и построить кривую.
к каноническому виду и построить кривую.
► По условию 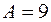 ,
, 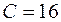


 уравнение эллипса. Выделим полные квадраты относительно
уравнение эллипса. Выделим полные квадраты относительно  и относительно
и относительно  .
.

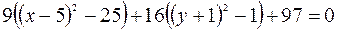


 – уравнение эллипса с центром в точке – уравнение эллипса с центром в точке 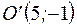 и с полуосями и с полуосями 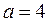 , , 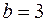 .◄ .◄
|
2) Привести общее уравнение 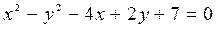 к каноническому виду и построить кривую.
к каноническому виду и построить кривую.
 ► По условию
► По условию  ,
, 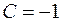

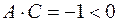
 уравнение гиперболы. Выделим полные квадраты относительно
уравнение гиперболы. Выделим полные квадраты относительно  и относительно
и относительно  .
. 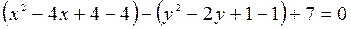


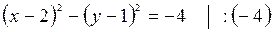

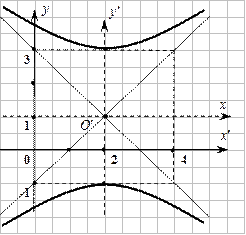
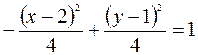 – уравнение гиперболы с центром в точке
– уравнение гиперболы с центром в точке 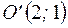 , действительная полуось
, действительная полуось 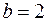 , мнимая полуось
, мнимая полуось  .◄
.◄
 3) Привести общее уравнение
3) Привести общее уравнение 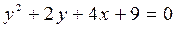 к каноническому виду и построить кривую.
к каноническому виду и построить кривую.
► По условию 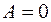
 уравнение параболы, ось симметрии которой параллельна
уравнение параболы, ось симметрии которой параллельна 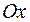 .
.
Выделим полный квадрат относительно  .
. 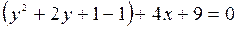

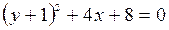

 – уравнение параболы с вершиной в точке
– уравнение параболы с вершиной в точке 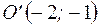 , параметр
, параметр  , ветви направлены влево. ◄
, ветви направлены влево. ◄
Типовой пример. Найти уравнение гиперболы с центром в начале координат и фокусами на оси ОХ, если прямая  проходит через левый фокус гиперболы и перпендикулярна ее асимптоте с отрицательным угловым коэффициентом.
проходит через левый фокус гиперболы и перпендикулярна ее асимптоте с отрицательным угловым коэффициентом.
► Из условия задачи следует, что каноническое уравнение искомой гиперболы имеет вид:
 ,
,
уравнения асимптот  , а фокусы
, а фокусы 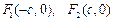 .
.
Так как заданная прямая проходит через левый фокус 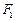 , то коэффициенты точки
, то коэффициенты точки 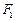 должны принадлежать уравнению прямой, т. е.
должны принадлежать уравнению прямой, т. е.
 и, следовательно,
и, следовательно, 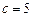 .
.
Для гиперболы 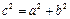 . Подставив найденное значение
. Подставив найденное значение  , получим первое уравнение относительно неизвестных
, получим первое уравнение относительно неизвестных 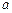 и
и 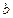 :
:
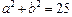 .
.
Второе уравнение мы найдем если запишем условие перпендикулярности заданной прямой в асимптоте с отрицательным угловым коэффициентом.
Пусть 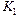 – угловой коэффициент заданной прямой,
– угловой коэффициент заданной прямой,  – угловой коэффициент асимптоты, тогда
– угловой коэффициент асимптоты, тогда  . Из уравнения прямой следует, что
. Из уравнения прямой следует, что 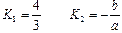
или  – условие перпендикулярности заданной прямой и асимптоты. Таким образом, для отыскания неизвестных величин
– условие перпендикулярности заданной прямой и асимптоты. Таким образом, для отыскания неизвестных величин  и
и 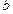 мы имеем:
мы имеем:
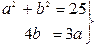
Решив эту систему, получим:  . Следовательно, искомое уравнение гиперболы имеет вид
. Следовательно, искомое уравнение гиперболы имеет вид
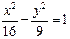 .◄
.◄
Пример. Два предприятия  и
и  , расстояние между которыми равно 200 км, производят некоторое изделие, заводская цена
, расстояние между которыми равно 200 км, производят некоторое изделие, заводская цена 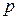 которого одна и та же для обоих предприятий. Транспортные расходы на перевозку единицы изделия от предприятия
которого одна и та же для обоих предприятий. Транспортные расходы на перевозку единицы изделия от предприятия  до потребителя
до потребителя 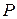 составляют 9 руб/км, а от предприятия
составляют 9 руб/км, а от предприятия  – 3 руб/км. Как следует разделить рынок сбыта, чтобы расходы потребителей были одинаковыми. Какому потребителю изделия какого предприятия выгоднее покупать?
– 3 руб/км. Как следует разделить рынок сбыта, чтобы расходы потребителей были одинаковыми. Какому потребителю изделия какого предприятия выгоднее покупать?
► Выберем прямоугольную систему координат, поместив начало координат в середине отрезка 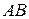 и направив оси координат по лучу
и направив оси координат по лучу 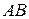 и перпендикуляру к нему (рис.3). Определим геометрическое место точек, в которых расходы потребителей на приобретение продукции предприятий
и перпендикуляру к нему (рис.3). Определим геометрическое место точек, в которых расходы потребителей на приобретение продукции предприятий  и
и  будут одинаковыми. Пусть потребитель находится в точке
будут одинаковыми. Пусть потребитель находится в точке 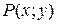 . Обозначим расстояния:
. Обозначим расстояния:  (км),
(км),  (км).
(км).
y
 P(x, y)
P(x, y)

 S1 S2
S1 S2


C A 0 В x
Тогда расходы на приобретение единицы изделия предприятия  составят
составят 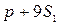 , а предприятия
, а предприятия  . Так как расходы потребителей должны быть одинаковы, то
. Так как расходы потребителей должны быть одинаковы, то 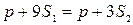 или
или  . (*)
. (*)
Используя координаты точек 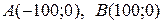 и
и 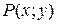 , вычислим значения
, вычислим значения 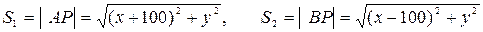 и подставим их в равенство (*), тогда:
и подставим их в равенство (*), тогда: 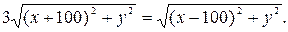
Отсюда получаем уравнение:
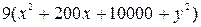 =
= 
или 

 .
.
Преобразуем это уравнение, разделив сначала обе части его на число 8, и затем выделив полные квадраты в левой части, тогда
 или
или 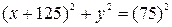 .
.
Последнее уравнение является уравнением окружности, с центром в точке 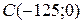 и радиусом
и радиусом 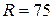 .
.
Для потребителей, находящихся на этой окружности,  , следовательно,
, следовательно, 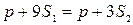 , поэтому расходы на приобретение изделия как одного, так и другого предприятия, одинаковы. Для потребителей, находящихся внутри ограниченного этой окружностью круга
, поэтому расходы на приобретение изделия как одного, так и другого предприятия, одинаковы. Для потребителей, находящихся внутри ограниченного этой окружностью круга  , следовательно,
, следовательно, 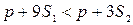 , поэтому расходы на приобретение изделий предприятия
, поэтому расходы на приобретение изделий предприятия  ниже. Аналогично можно установить, что для потребителей, находящихся вне этого круга, ниже расходы на приобретение изделий предприятия
ниже. Аналогично можно установить, что для потребителей, находящихся вне этого круга, ниже расходы на приобретение изделий предприятия  .
.
Следовательно, рынок сбыта можно выгодно (экономично) поделить так: а) потребителям, находящимся на окружности, безразлично, изделия какого предприятия (  или
или  ) покупать; б) потребители, находящиеся внутри указанного круга, покупают изделия предприятия
) покупать; б) потребители, находящиеся внутри указанного круга, покупают изделия предприятия  ; в) потребители, находящиеся вне круга, покупают изделия предприятия
; в) потребители, находящиеся вне круга, покупают изделия предприятия  .◄
.◄
Пример. Кооператив, объединяющий х работников–исполнителей заказов и одного заведующего, имеет в месяц 3 000 рублей фонда заработной платы. Записать формулу для размера заработной платы каждого сотрудника кооператива, если ее размер одинаков и для каждого работника, и для заведующего. Каков размер заработной платы, если в кооперативе 9 работников – исполнителей заказов?
► Чтобы подсчитать размер  заработной платы, следует фонд 3 000 рублей разделить на число
заработной платы, следует фонд 3 000 рублей разделить на число 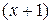 сотрудников, поэтому
сотрудников, поэтому  – искомая формула. Эта формула имеет вид (2), следовательно, ей соответствует гипербола, горизонтальной асимптотой которой является ось ОХ, а вертикальной – прямая
– искомая формула. Эта формула имеет вид (2), следовательно, ей соответствует гипербола, горизонтальной асимптотой которой является ось ОХ, а вертикальной – прямая 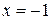 .
.
При 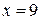 имеем
имеем  (руб).◄
(руб).◄
Пример. В условиях предыдущего примера предполагается, что кооператив решил производить отчисления по 50 руб. в месяц с каждого сотрудника в фонд дальнейшего развития своего предприятия. Как запишется при этом формула для заработной платы сотрудника?
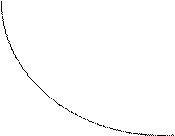
► Так как теперь каждый сотрудник будет получать на 50 рублей меньше, чем в условиях примера 2, то 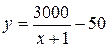 – искомая формула. Значит ей соответствует гипербола, горизонтальной асмптотой которой является прямая
– искомая формула. Значит ей соответствует гипербола, горизонтальной асмптотой которой является прямая  , а вертикальной – прямая
, а вертикальной – прямая 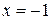 .◄
.◄

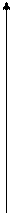 y
y
– 1 x
– 50
Пример. Пусть в момент 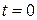 началось производство определенного типа машин, которые раньше не производились. Допустим, что выпуск машин происходит равномерно, стоимость годового объема выпуска их составляет 5 млн. рублей, а срок эксплуатации машин равен 10 годам. Определить стоимость всех машин этого типа на конец
началось производство определенного типа машин, которые раньше не производились. Допустим, что выпуск машин происходит равномерно, стоимость годового объема выпуска их составляет 5 млн. рублей, а срок эксплуатации машин равен 10 годам. Определить стоимость всех машин этого типа на конец 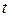 -го года. Подсчитать эту стоимость на конец 4-го года.
-го года. Подсчитать эту стоимость на конец 4-го года.
► Стоимость всех машин указанного типа в 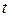 –ом году без учета износа составляет 5 · 106 ·
–ом году без учета износа составляет 5 · 106 · 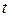 (руб.). Однако вследствие износа фактическая стоимость их будет значительно меньше. Среди всех действующих к моменту
(руб.). Однако вследствие износа фактическая стоимость их будет значительно меньше. Среди всех действующих к моменту 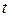 машин имеются такие, которые поступили в начале интервала времени
машин имеются такие, которые поступили в начале интервала времени 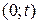 , а также такие, которые поступили только что. Поскольку поступление машин происходило равномерно, то средний возраст всех машин можно считать равным
, а также такие, которые поступили только что. Поскольку поступление машин происходило равномерно, то средний возраст всех машин можно считать равным  . Амортизация на каждую действующую машину накапливается равномерно. Ввиду 10-летнего срока эксплуатации в данном примере ежегодное накопление составляет 10% (одну десятую часть) стоимости машины. Ежегодные амортизационные накопления на все машины, действующие к моменту
. Амортизация на каждую действующую машину накапливается равномерно. Ввиду 10-летнего срока эксплуатации в данном примере ежегодное накопление составляет 10% (одну десятую часть) стоимости машины. Ежегодные амортизационные накопления на все машины, действующие к моменту 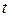 , составляют 10% от их стоимости, или
, составляют 10% от их стоимости, или 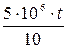 . А так как средний возраст всех машин равен
. А так как средний возраст всех машин равен 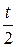 лет, то амортизационные отчисления на все машины, действующие к моменту
лет, то амортизационные отчисления на все машины, действующие к моменту 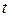 , составят
, составят 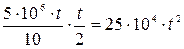 (руб). Вычитая эту сумму из стоимости без учета износа, получим фактическую стоимость всех машин на конец
(руб). Вычитая эту сумму из стоимости без учета износа, получим фактическую стоимость всех машин на конец 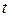 t – го года, т.е. искомая стоимость составляет:
t – го года, т.е. искомая стоимость составляет: 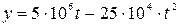 (руб.). Это целая рациональная функция второго порядка (квадратичная функция) вида
(руб.). Это целая рациональная функция второго порядка (квадратичная функция) вида 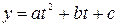 с коэффициентами:
с коэффициентами: 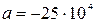 ;
;  ;
; 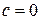 .
.
Стоимость всех машин на конец 4-го года будет равна
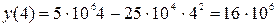 (руб) или 16 млн руб.◄
(руб) или 16 млн руб.◄
Пример. Построить графики функций спроса  и предложения
и предложения 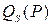 и найти точку равновесия, если
и найти точку равновесия, если 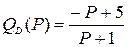 ;
; 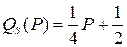 .
.
► Построим в плоскости РОQ графики функций спроса и предложения (см. рис.).
 В точке равновесия
В точке равновесия 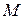 (точке пересечения графиков) спрос равен предложению. Для нахождения координат этой точки решим систему:
(точке пересечения графиков) спрос равен предложению. Для нахождения координат этой точки решим систему:
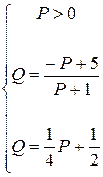 .
.
Из этой системы получаем
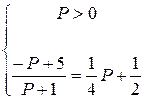 Þ
Þ 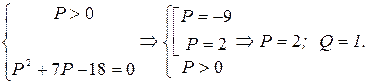 ◄
◄
Поверхности второго порядка
Поверхности второго порядка в прямоугольной системе координат определяются алгебраическими уравнениями второй степени.
По заданному уравнению поверхности будем определять ее внешний вид методом сечений, т.е. будем находить линии пересечения поверхности с координатными плоскостями или с плоскостями, параллельными координатным плоскостям.
1. Эллипсоид.Каноническое уравнение эллипсоида имеет вид
 .
.
1) Находим линию пересечения эллипсоида с плоскостью 
 .
.
Решаем систему уравнений
 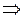 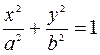
|
- это уравнение эллипса
с полуосями  и и  . .
|
 2) Находим линию пересечения эллипсоида с плоскостью
2) Находим линию пересечения эллипсоида с плоскостью 
 .
.
Решаем систему уравнений

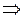
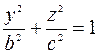 –
–
это уравнение эллипса с полуосями
 и
и  .
.
3) Находим линию пересечения эллипсоида с плоскостью 
 .
.
Решаем систему уравнений

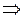
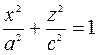
– это уравнение эллипса с полуосями  и
и  .
.
Эллипсоид – это замкнутая овальная поверхность.  ,
,  ,
,  – полуоси эллипсоида. Если
– полуоси эллипсоида. Если  , то эллипсоид превращается в сферу.
, то эллипсоид превращается в сферу.
2. Однополостный гиперболоид.Каноническое уравнение имеет вид
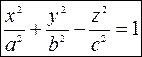
Строим методом сечений.
1) Находим линию пересечения с плоскостью  .
.
Решаем систему уравнений 

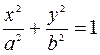
- это уравнение эллипса с полуосями  и
и  .
.
2) Находим линии пересечения с плоскостями, параллельными плоскости  :
: 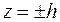
Решаем систему уравнений



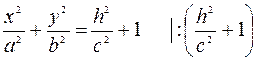
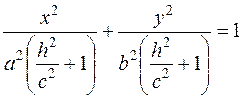
- это уравнение эллипса с полуосями  и
и  .
.
3) Находим линию пересечения с плоскостью  .
.
Решаем систему уравнений 

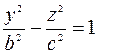 - это уравнение гиперболы, где
- это уравнение гиперболы, где  – действительная полуось, а
– действительная полуось, а  - мнимая полуось.
- мнимая полуось.
4) Находим линию пересечения с плоскостью  . Решаем систему уравнений
. Решаем систему уравнений


 - это уравнение гиперболы.
- это уравнение гиперболы.
 - действительная полуось, а
- действительная полуось, а  – мнимая полуось.
– мнимая полуось.
Однополостный гиперболоид – это бесконечная труба, которая бесконечно расширяется по мере удаления от плоскости  .
.  ,
,  ,
,  – это полуоси гиперболоида. Полуось
– это полуоси гиперболоида. Полуось  увидим, если построим основной прямоугольник какой-либо из гипербол.
увидим, если построим основной прямоугольник какой-либо из гипербол.
3. Двуполостный гиперболоид.Каноническое уравнение имеет вид
 .
.
1) Находим линию пересечения с плоскостью  .
.
Решаем систему уравнений:
  
|
– это уравнение мнимого эллипса.
|
Следовательно, с плоскостью  нет общих точек.
нет общих точек.
2) Находим линии пересечения с плоскостями, параллельными плоскости  :
: 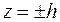 .
.
а) Решаем систему уравнений 

 – это уравнение мнимого эллипса, так как
– это уравнение мнимого эллипса, так как  .
.
б) Решаем систему уравнений



 .
.
Получим точки  и
и 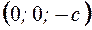 .
.
в) Решаем систему уравнений


 ;
;
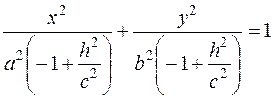
– это уравнение эллипса, с полуосями  и
и  .
.
2) Находим линию пересечения с плоскостью  .
.
Решаем систему уравнений 

 .
.
Это уравнение гиперболы, где  -действительная полуось, а
-действительная полуось, а  - мнимая полуось.
- мнимая полуось.
3) Находим линию пересечения с плоскостью  . Решаем систему уравнений
. Решаем систему уравнений


 - это уравнение гиперболы,
- это уравнение гиперболы,
где  - действительная полуось, а
- действительная полуось, а  – мнимая полуось.
– мнимая полуось.
Двуполостный гиперболоид – это две чаши с вершинами в точках 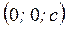 и
и  , которые бесконечно расширяются по мере удаления от плоскости
, которые бесконечно расширяются по мере удаления от плоскости  .
.  ,
,  и
и  - полуоси гиперболы. Полуоси
- полуоси гиперболы. Полуоси  и
и  увидим, если построим основные прямоугольники обеих гипербол.
увидим, если построим основные прямоугольники обеих гипербол.
4. Эллиптический параболоид.Каноническое уравнение имеет вид
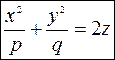 ,
,
где  и
и 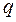 это параметры параболоида,
это параметры параболоида,  ;
; 

