Свойства смешанного произведения
Свойства смешанного произведения
1.  . Данное равенство
. Данное равенство 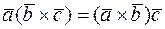 позволяет обозначать смешанное произведение векторов
позволяет обозначать смешанное произведение векторов  ,
,  ,
, 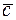 символом
символом 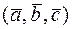 , не указывая при этом, какие именно два вектора (первые или последние) перемножаются векторно.
, не указывая при этом, какие именно два вектора (первые или последние) перемножаются векторно.
2. Величина векторного произведения не изменяется при циклической перестановке сомножителей:

3. 
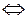 векторы
векторы  компланарны.
компланарны.
4. Смешанное произведение линейно по каждому из сомножителей. В частности,
 .
.
Выражение векторного произведения через координаты сомножителей.
Теорема. Если векторы  заданы своими координатами:
заданы своими координатами:  ,
, 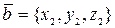 ,
,  , то смешанное произведение
, то смешанное произведение 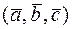 равняется определителю, строки которого соответственно равны координатам перемножаемых векторов, т.е.
равняется определителю, строки которого соответственно равны координатам перемножаемых векторов, т.е.
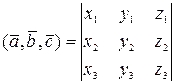 .
.
Действительно,  . Тогда
. Тогда

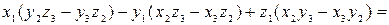

 .
.
Типовой пример. Даны точки A(4; -1; 3), B(0; 1; 2), C(3; -2; 5), D(1; -1; 1). Найти: а) площадь треугольника АВС; б) высоту  треугольника АВС, опущенную из вершины А на сторону ВС; в) объём пирамиды АВСD.
треугольника АВС, опущенную из вершины А на сторону ВС; в) объём пирамиды АВСD.
► а) Площадь  треугольника АВС равна половине площади параллелограмма S, построенного на векторах
треугольника АВС равна половине площади параллелограмма S, построенного на векторах  и
и  , т.е.
, т.е.  . Имеем
. Имеем  ,
, 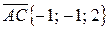 ,
,

 ;
;
б)  ;
;  ,
,  ;
;  ;
;
в) Объём  пирамиды АВСD равен
пирамиды АВСD равен 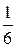 объёма параллелепипеда, построенного на векторах
объёма параллелепипеда, построенного на векторах  . Имеем
. Имеем 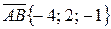 ,
, 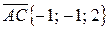 ,
,  ;
;
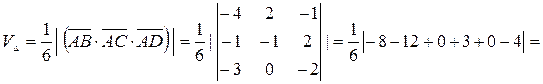
 .◄
.◄
Типовой пример. Даны координаты вершин пирамиды  .
.
► 1) Найти длину ребра  .
.

2) Найти угол между ребрами  и
и  .
.

3) Найти угол между ребром  и гранью
и гранью 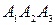 . Сначала найдем вектор нормали к грани
. Сначала найдем вектор нормали к грани 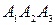
 как векторное произведение векторов
как векторное произведение векторов  и
и  .
.
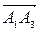 = (2-1; 1-0; 1-3) = (1; 1; -2),
= (2-1; 1-0; 1-3) = (1; 1; -2),

Найдем угол между вектором нормали и вектором  .
.
 ,
,  -4 – 4 = -8.
-4 – 4 = -8.
Искомый угол g между вектором и плоскостью будет равен g = 900 – b.
 .
.
4) Найти площадь грани 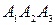
 .
.
5) Найти объем пирамиды.
 (ед3).◄
(ед3).◄
Прямая на плоскости
Общее уравнение прямой на плоскости
Пусть в системе координат  задана прямая
задана прямая  , проходящая через точку
, проходящая через точку  , и задан ненулевой вектор
, и задан ненулевой вектор 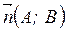 , перпендикулярный прямой
, перпендикулярный прямой  . Произвольная точка
. Произвольная точка  будет лежать на прямой
будет лежать на прямой  тогда и только тогда, когда
тогда и только тогда, когда  ,
,  . Из условия перпендикулярности векторов следует, что
. Из условия перпендикулярности векторов следует, что
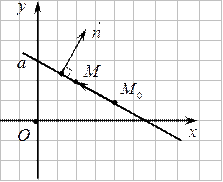 
| (1) – уравнение прямой, проходящей через данную точку и перпендикулярной данному вектору.
|
Преобразуем уравнение (1): 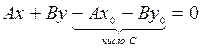
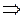

| (2) – общее уравнение прямой.
|
Вектор 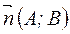 называется нормальным вектором прямой
называется нормальным вектором прямой  .
.
Частные случаи расположения прямой на плоскости.
Уравнение в отрезках на осях.
Пусть прямая  задана общим уравнением
задана общим уравнением  .
.
Если  , то прямая проходит через начало координат;
, то прямая проходит через начало координат;
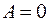 , то
, то  ;
;
 , то
, то  ;
;
Если  , то
, то 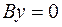
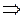
 – это ось
– это ось  ;
;
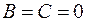 , то
, то 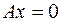
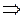
 – это ось
– это ось  ;
;
Если  .
.
 можно преобразовать к виду
можно преобразовать к виду 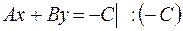 ,
,

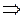
 , обозначим
, обозначим 
Получим 
| (3) – уравнение прямой в отрезках на осях,
|
где 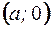 и
и 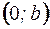 – точки пересечения с осями координат. Уравнение (3) используется при построении прямой в системе координат
– точки пересечения с осями координат. Уравнение (3) используется при построении прямой в системе координат 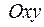 .
.
Типовой пример. Построить прямую 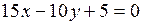 .
.
 ► Приведем уравнение
► Приведем уравнение 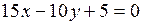 к уравнению в отрезках на осях:
к уравнению в отрезках на осях:

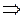
 . ◄
. ◄
Типовой пример. Построить прямую  .
.

► Приведем уравнение  к уравнению в отрезках на осях
к уравнению в отрезках на осях
 ,
,  ,
, 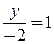 . ◄
. ◄
 3. Уравнение прямой, проходящей через данную точку: а) параллельной данной прямой; б) перпендикулярной данной прямой
3. Уравнение прямой, проходящей через данную точку: а) параллельной данной прямой; б) перпендикулярной данной прямой
а) Пусть прямая  задана общим уравнением
задана общим уравнением 
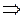
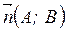 , а прямая
, а прямая  параллельна прямой
параллельна прямой  и проходит через точку
и проходит через точку  . Составим уравнение прямой
. Составим уравнение прямой  . Произвольная точка
. Произвольная точка  будет лежать на прямой
будет лежать на прямой  , если
, если  ,
,  . Из условия перпендикулярности векторов получим уравнение прямой
. Из условия перпендикулярности векторов получим уравнение прямой  .
.

| (4) – уравнение прямой, проходящей через
данную точку и параллельной данной
прямой.
|
б) Пусть прямая  задана общим уравнением
задана общим уравнением 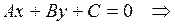
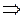
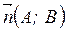 , а прямая
, а прямая  перпендикулярна прямой
перпендикулярна прямой  и проходит через точку
и проходит через точку  . Составим уравнение прямой
. Составим уравнение прямой  . Произвольная точка
. Произвольная точка  будет принадлежать прямой
будет принадлежать прямой  , если
, если  ,
,  . Из условия коллинеарности векторов получаем уравнение прямой
. Из условия коллинеарности векторов получаем уравнение прямой  .
.

| (5) – уравнение прямой, проходящей через данную точку и перпендикулярной данной прямой
|
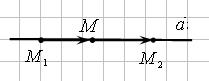 4. Уравнение прямой, проходящей через две точки
4. Уравнение прямой, проходящей через две точки
Пусть точки  и
и  лежат на прямой
лежат на прямой  . Произвольная точка
. Произвольная точка  будет лежать на прямой
будет лежать на прямой  тогда и только тогда, когда
тогда и только тогда, когда  ,
,  ,
, 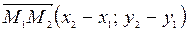 .
.
Из условия коллинеарности векторов получим уравнение.

| (6) – уравнение прямой, проходящей через
две точки
|
Параметрическое уравнение
Пусть в каноническом уравнении  , где
, где 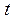 – параметр,
– параметр,  .
.
Тогда 

| 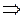 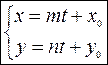
| (8) – параметрические
уравнения прямой
|
Придавая в (8) параметру  конкретные значения, мы будем получать координаты точек, лежащих на прямой.
конкретные значения, мы будем получать координаты точек, лежащих на прямой.
Плоскость
1. Общее уравнение плоскости. Пусть заданы: система координат  , плоскость
, плоскость  , точка
, точка  и вектор
и вектор 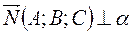 . Произвольная точка
. Произвольная точка  принадлежит плоскости
принадлежит плоскости  тогда и только тогда, когда векторы
тогда и только тогда, когда векторы  и
и  будут перпендикулярны, т.е.
будут перпендикулярны, т.е. 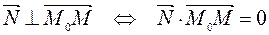 . Координаты векторов:
. Координаты векторов:  ,
, 
 . Следовательно,
. Следовательно,
 (1) – уравнение плоскости, проходящей через данную точку, перпендикулярной данному вектору, где
(1) – уравнение плоскости, проходящей через данную точку, перпендикулярной данному вектору, где 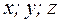 – текущие координаты;
– текущие координаты;  - координаты точки
- координаты точки 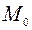 ;
; 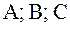 – координаты вектора
– координаты вектора  . Преобразуем уравнение (1).
. Преобразуем уравнение (1).
 . Получим
. Получим  (2) – общее уравнение плоскости
(2) – общее уравнение плоскости  .
.
Из общего уравнения получаем вектор  , называемый нормальным вектором плоскости
, называемый нормальным вектором плоскости  .
.
Типовой пример. Составить уравнение плоскости, проходящей через точку 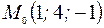 перпендикулярной вектору
перпендикулярной вектору  .
.
► Применяя уравнение (1), получим:  ;
;
 или
или 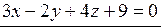 – это и есть общее уравнение плоскости. ◄
– это и есть общее уравнение плоскости. ◄
Пучок плоскостей
Пусть плоскости  и
и 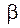 пересекаются по прямой a.
пересекаются по прямой a.


Плоскости, проходящие через линию пересечения двух плоскостей, образуют пучок плоскостей. Уравнение пучка плоскостей: 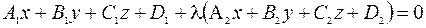 .
.
 Чтобы написать уравнение какой-либо плоскости пучка, достаточно знать точку, через которую она проходит.
Чтобы написать уравнение какой-либо плоскости пучка, достаточно знать точку, через которую она проходит.
Типовой пример. Написать уравнение плоскости  , проходящей через линию пересечения плоскостей
, проходящей через линию пересечения плоскостей  и
и  , и через точку
, и через точку 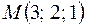 .
.
► Запишем уравнение пучка плоскостей:  .
.
 Значение
Значение  определяем из условия, что плоскость проходит через точку
определяем из условия, что плоскость проходит через точку 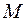 :
:  , или
, или 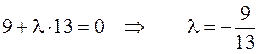 .
.
Следовательно, искомое уравнение имеет вид:
 или
или  . ◄
. ◄
Прямая в пространстве
Общие уравнения прямой
Прямая может быть задана как линия пересечения двух плоскостей.

|

| 
| (1) – общие
уравнения
прямой  . .
|
2. Канонические уравнения прямой
Пусть заданы прямая  , точка
, точка  и вектор
и вектор 
 .
.
Произвольная точка  лежит на прямой
лежит на прямой  , если
, если 

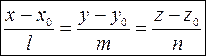 (2) – канонические уравнения прямой
(2) – канонические уравнения прямой  .
.
3десь:  – текущие координаты,
– текущие координаты,  - координаты точки
- координаты точки  ,
, 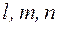 – координаты вектора
– координаты вектора  .
.
Типовой пример. Привести общие уравнения прямой  к каноническому виду.
к каноническому виду.
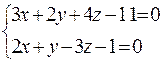 .
.
► 1-й способ. 1) Найдем точку  , принадлежащую прямой
, принадлежащую прямой  .
.
Предположим, что  и решим систему
и решим систему
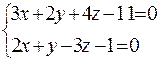 ,
, 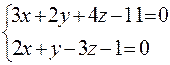

 .
.
2) Найдем вектор  , параллельный прямой
, параллельный прямой  . Так как он должен быть перпендикулярен векторам
. Так как он должен быть перпендикулярен векторам  и
и  , то за
, то за  можно принять векторное произведение векторов
можно принять векторное произведение векторов 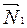 и
и 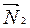 .
. 

 , где
, где 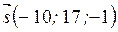 .
.
Искомая прямая определяется уравнениями  . ◄
. ◄
► 2-й способ. Найдем две точки  и
и  искомой прямой.
искомой прямой.
Предположим, что  и решим систему
и решим систему
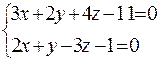 ,
, 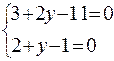

 .
.
 ( см. 1 способ решения).
( см. 1 способ решения).
Записываем уравнения прямой  , проходящей через точки
, проходящей через точки  и
и 

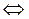
 . ◄
. ◄
Типовой пример. Написать канонические и параметрические уравнения прямой  , проходящей через точку
, проходящей через точку 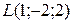 , параллельной оси ОУ.
, параллельной оси ОУ.
► Так как искомая прямая  параллельна оси ОУ, то в качестве ее направляющего вектора можно взять вектор
параллельна оси ОУ, то в качестве ее направляющего вектора можно взять вектор  (здесь этот вектор можно рассматривать как направляющий вектор оси ОУ).
(здесь этот вектор можно рассматривать как направляющий вектор оси ОУ).
Получаем уравнения прямой  :
:
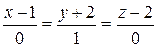 – канонические;
– канонические;
 – параметрические.◄
– параметрические.◄
Поверхности второго порядка
Поверхности второго порядка в прямоугольной системе координат определяются алгебраическими уравнениями второй степени.
По заданному уравнению поверхности будем определять ее внешний вид методом сечений, т.е. будем находить линии пересечения поверхности с координатными плоскостями или с плоскостями, параллельными координатным плоскостям.
1. Эллипсоид. Каноническое уравнение эллипсоида имеет вид
 .
.
1) Находим линию пересечения эллипсоида с плоскостью 
 .
.
Решаем систему уравнений
 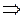 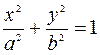
|
- это уравнение эллипса
с полуосями  и и  . .
|
 2) Находим линию пересечения эллипсоида с плоскостью
2) Находим линию пересечения эллипсоида с плоскостью 
 .
.
Решаем систему уравнений

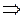
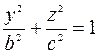 –
–
это уравнение эллипса с полуосями
 и
и  .
.
3) Находим линию пересечения эллипсоида с плоскостью 
 .
.
Решаем систему уравнений

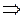
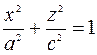
– это уравнение эллипса с полуосями  и
и  .
.
Эллипсоид – это замкнутая овальная поверхность.  ,
,  ,
,  – полуоси эллипсоида. Если
– полуоси эллипсоида. Если  , то эллипсоид превращается в сферу.
, то эллипсоид превращается в сферу.
2. Однополостный гиперболоид. Каноническое уравнение имеет вид
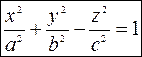
Строим методом сечений.
1) Находим линию пересечения с плоскостью  .
.
Решаем систему уравнений 

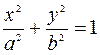
- это уравнение эллипса с полуосями  и
и  .
.
2) Находим линии пересечения с плоскостями, параллельными плоскости  :
: 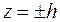
Решаем систему уравнений



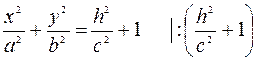
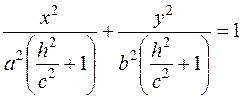
- это уравнение эллипса с полуосями  и
и  .
.
3) Находим линию пересечения с плоскостью  .
.
Решаем систему уравнений 

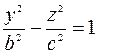 - это уравнение гиперболы, где
- это уравнение гиперболы, где  – действительная полуось, а
– действительная полуось, а  - мнимая полуось.
- мнимая полуось.
4) Находим линию пересечения с плоскостью  . Решаем систему уравнений
. Решаем систему уравнений


 - это уравнение гиперболы.
- это уравнение гиперболы.
 - действительная полуось, а
- действительная полуось, а  – мнимая полуось.
– мнимая полуось.
Однополостный гиперболоид – это бесконечная труба, которая бесконечно расширяется по мере удаления от плоскости  .
.  ,
,  ,
,  – это полуоси гиперболоида. Полуось
– это полуоси гиперболоида. Полуось  увидим, если построим основной прямоугольник какой-либо из гипербол.
увидим, если построим основной прямоугольник какой-либо из гипербол.
3. Двуполостный гиперболоид. Каноническое уравнение имеет вид
 .
.
1) Находим линию пересечения с плоскостью  .
.
Решаем систему уравнений:
  
|
– это уравнение мнимого эллипса.
|
Следовательно, с плоскостью  нет общих точек.
нет общих точек.
2) Находим линии пересечения с плоскостями, параллельными плоскости  :
: 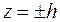 .
.
а) Решаем систему уравнений 

 – это уравнение мнимого эллипса, так как
– это уравнение мнимого эллипса, так как  .
.
б) Решаем систему уравнений



 .
.
Получим точки  и
и 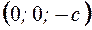 .
.
в) Решаем систему уравнений


 ;
;
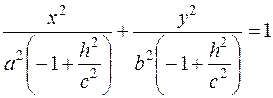
– это уравнение эллипса, с полуосями  и
и  .
.
2) Находим линию пересечения с плоскостью  .
.
Решаем систему уравнений 

 .
.
Это уравнение гиперболы, где  -действительная полуось, а
-действительная полуось, а  - мнимая полуось.
- мнимая полуось.
3) Находим линию пересечения с плоскостью  . Решаем систему уравнений
. Решаем систему уравнений


 - это уравнение гиперболы,
- это уравнение гиперболы,
где  - действительная полуось, а
- действительная полуось, а  – мнимая полуось.
– мнимая полуось.
Двуполостный гиперболоид – это две чаши с вершинами в точках 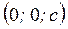 и
и  , которые бесконечно расширяются по мере удаления от плоскости
, которые бесконечно расширяются по мере удаления от плоскости  .
.  ,
,  и
и  - полуоси гиперболы. Полуоси
- полуоси гиперболы. Полуоси  и
и  увидим, если построим основные прямоугольники обеих гипербол.
увидим, если построим основные прямоугольники обеих гипербол.
4. Эллиптический параболоид. Каноническое уравнение имеет вид
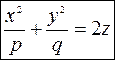 ,
,
где  и
и 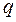 это параметры параболоида,
это параметры параболоида,  ;
;  ,
,
Строим методом сечений.
1) Находим линию пересечения с плоскостью  . Решаем систему уравнений
. Решаем систему уравнений
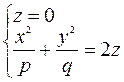

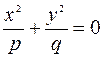 – это уравнение точки
– это уравнение точки 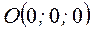 .
.
 2) Находим линии пересечения с плоскостями, параллельными
2) Находим линии пересечения с плоскостями, параллельными
плоскости  . Решаем систему уравнений:
. Решаем систему уравнений:
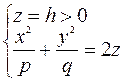


 – это уравнение эллипса с полуосями
– это уравнение эллипса с полуосями  и
и  . При
. При  получим уравнение мнимого эллипса.
получим уравнение мнимого эллипса.
3) Находим линию пересечения с плоскостью  . Решаем систему уравнений
. Решаем систему уравнений


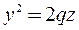 – это уравнение параболы симметричной относительно оси
– это уравнение параболы симметричной относительно оси  .
.
4) Аналогично найдем линию пересечения с плоскостью  . Это будет парабола
. Это будет парабола 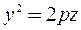 симметричная относительно оси
симметричная относительно оси  . Если
. Если  , то получаем параболоид вращения.
, то получаем параболоид вращения.
5. Гиперболический параболоид. Каноническое уравнение имеет вид
 ,
,
где  и
и 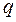 – это параметры параболоида,
– это параметры параболоида,  ;
;  ,
,
Строим методом сечений. 1) Находим линию пересечения с плоскостью  . Решаем систему уравнений
. Решаем систему уравнений



 – это уравнение параболы, симметричной относительно оси
– это уравнение параболы, симметричной относительно оси  .
.
2)Находим линию пересечения с плоскостью  . Решаем систему уравнений
. Решаем систему уравнений


 – это уравнение параболы, симметричной относительно оси
– это уравнение параболы, симметричной относительно оси  .
.
3) Находим линии пересечения с плоскостями, параллельными плоскости  .
.
а) Решаем систему уравнений
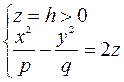


 – это уравнение гиперболы, у которой
– это уравнение гиперболы, у которой  - действительная полуось, а
- действительная полуось, а  - мнимая полуось.
- мнимая полуось.
б) Решаем систему уравнений


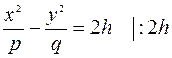
 ( знак левой части изменился, так как
( знак левой части изменился, так как  по условию) – это уравнение гиперболы, у которой
по условию) – это уравнение гиперболы, у которой 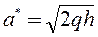 – действительная полуось, а
– действительная полуось, а 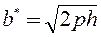 – мнимая полуось.
– мнимая полуось.
4) Находим линию пересечения с плоскостью  .
.
Решаем систему уравнений


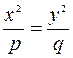 – это уравнение двух прямых, проходящих через точку
– это уравнение двух прямых, проходящих через точку 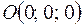 .
.
Гиперболический параболоид – это поверхность, имеющая вид седла.
6. Конус второго порядка. Каноническое уравнение имеет вид
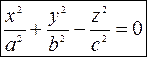
Строим методом сечений.
1) Находим линию пересечения с плоскостью 
 . Решаем систему уравнений
. Решаем систему уравнений



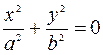 – это уравнение точки
– это уравнение точки  .
.
2) Находим линии пересечения с плоскостями параллельными 
 . Решаем систему уравнений
. Решаем систему уравнений
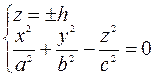
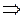
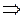

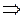
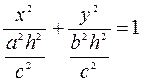 – это уравнение эллипса с полуосями
– это уравнение эллипса с полуосями  и
и  .
.
3) Находим линию пересечения с плоскостью 
 . Решаем систему уравнений
. Решаем систему уравнений

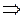
 – это уравнение двух прямых, проходящих через начало координат.
– это уравнение двух прямых, проходящих через начало координат.
4) Находим линию пересечения с плоскостью 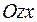
 . Решаем систему уравнений
. Решаем систему уравнений


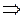
 – это уравнение двух прямых, проходящих через начало координат.
– это уравнение двух прямых, проходящих через начало координат.
7. Цилиндрические поверхности. Задаются уравнениями:
Популярное:

