Предпосылки к расчету зубчатых передач на контактные напряжения.

Впервые контактную задачу выполнил и решил Г.Герц (Herz), рассмотрев сжатие двух цилиндров под действием распределенной нагрузки q (рис.8).

Рис. 8

Первоначальный контакт осуществляется по линии у-у. При сжатии цилиндров распределенной по длине нагрузкой в результате упругой деформации образуется площадка контакта в виде прямоугольника шириной 2а.

Наибольшее напряжение на поверхности контакта

Мпа. (2.1)

Формула справедлива при условии следующих допущений:

1. действующие усилия направлены нормально к поверхности соприкосновения цилиндров;

2. нагрузка распределена равномерно по поверхности контактирующих цилиндров q=const;

3. силы трения отсутствуют;

4. материалы соприкасающихся тел однородны и изотропны;

5. поверхности абсолютно гладкие.

В формуле (2.1) МПа – приведенный модуль упругости, а Е₁ и Е₂ – модули упругости материала цилиндров,

- приведенный радиус кривизны; μ – коэффициент Пуассона материала цилиндров μ =0, 3.

 

Расчет зубчатых передач на контактную выносливость.

Наибольшие контактные напряжения возникают в тонком поверхностном слое материала. Толщина этого слоя составляет (0, 2…0, 3)m.

В качестве исходной принимают формулу Герца (2.1)

где - допускаемое контактное напряжение, зависящее от материала колес, химико-термической обработки и технологии изготовления зубчатого колеса.

– расчетная нормальная нагрузка, Н/мм.

Подставляя величины и 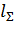, получим:

, или

Н/мм, (2.2)

где – коэффициент нагрузки.

 

Расчетная нагрузка и проверочный расчет на контактную выносливость

Расчетная нагрузка складывается из:

1. Полезной или номинальной в предположении равномерного распределения её по длине линии контакта (рис.9).

 

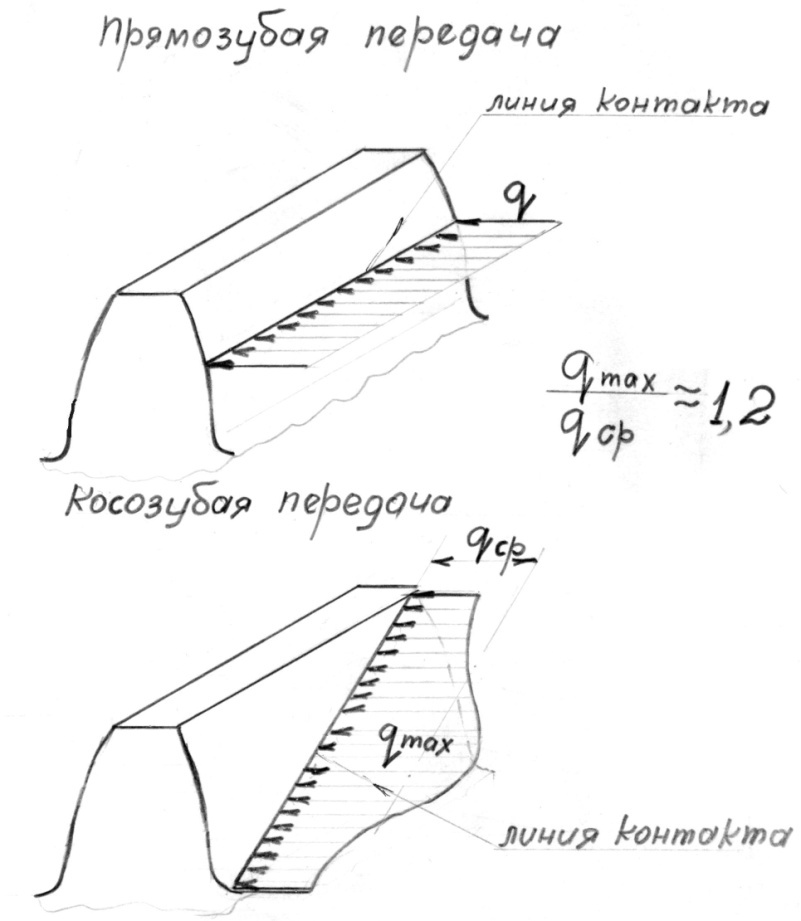
Рис. 9

 

 

2. Дополнительной нагрузки вызванной перераспределением номинальной нагрузки по длине линии контакта вследствие упругих деформаций системы, погрешностей изготовления и монтажа и др. факторов. Таким образом

. (2.3)

Здесь - коэффициент концентрации, т.е. неравномерности действия нагрузки. Неравномерность тем меньше, чем меньше длинна линий контакта и жесткость зуба, чем больше жесткость валов и опор, выше прорабатываемость зубьев и симметричность расположения колес относительно опор, выше точность изготовления и монтажа.

 

Значение определяется из рисунка 10.

 

График для определения ориентировочных значений коэффициента Kнβ (цифры у кривых соответствуют передачам на схемах), для режимов с V< 15 м/с. 1- шариковые опоры, 2- роликовые опоры.

 

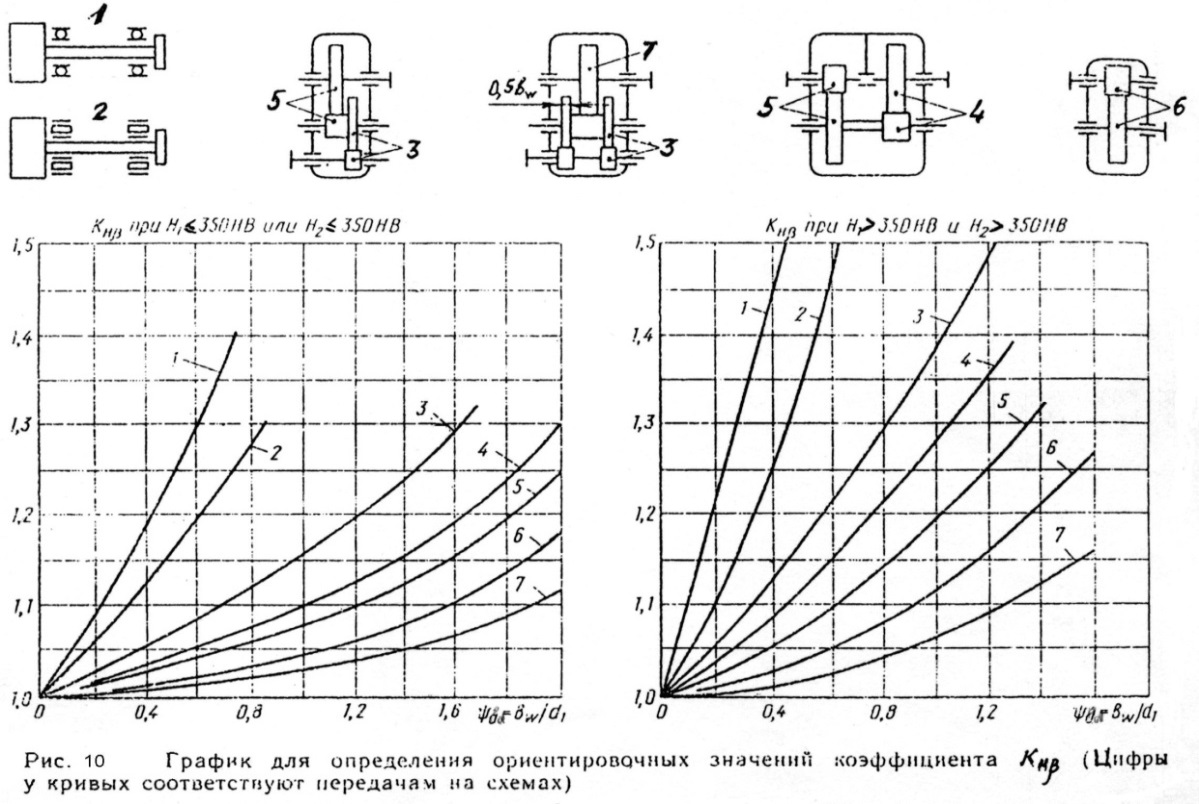
Рис.10
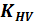- коэффициент динамической нагрузки. Учитывает погрешность зацепления основного шага зубьев, деформации от изгиба зубьев и опор под нагрузкой, влияние пересопряжений, которые вызывают неравномерность вращения колеса при равномерном вращении шестерни. Если окружной шаг зубьев шестерни меньше шага зубьев колеса , то контакт возникает в точке В (рис.11). В результате деформации зубьев шаг выравнивается, возникает удар, кратковременное изменение передаточного числа, возрастает мгновенная нагрузка на зуб.

 

Коэффициент динамической нагрузки 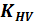тем меньше, чем выше степень точности изготовления, и увеличивается с повышением скорости вращения зубчатых колес.

 

Рис. 11

Коэффициент динамической нагрузки находится из табл.3

Таблица 3

Степень точности	Коэффициент	Окружная скорость, v, м/с
	KHv	1, 03	1, 06	1, 12	1, 17	1, 23	1, 28
1, 01	1, 02	1, 03	1, 04	1, 06	1, 07
KFv	1, 06	1, 13	1, 26	1, 40	1, 58	1, 67
1, 02	1, 05	1, 10	1, 15	1, 20	1, 25
	KHv	1, 04	1, 07	1, 14	1, 21	1, 29	1, 36
1, 02	1, 03	1, 05	1, 06	1, 07	1, 08
KFv	1, 08	1, 16	1, 33	1, 50	1, 67	1, 80
1, 03	1, 06	1, 11	1, 16	1, 22	1, 27
	KHv	1, 04	1, 08	1, 16	1, 24	1, 32	1, 40
1, 01	1, 02	1, 04	1, 06	1, 07	1, 08
KFv	1, 10	1, 20	1, 38	1, 58	1, 78	1, 96
1, 03	1, 06	1, 11	1, 17	1, 23	1, 29
	KHv	1, 05	1, 10	1, 20	1, 30	1, 40	1, 50
1, 01	1, 03	1, 05	1, 07	1, 90	1, 12
KFv	1, 13	1, 28	1, 50	1, 77	1, 98	2, 25
1, 04	1, 07	1, 14	1, 21	1, 28	1, 36

- коэффициент неравномерности распределения нагрузки между зубьями. Зависит от податливости пары зубьев и их склонности к приработке. определяется по табл.4

 

 

Таблица 4

 

Заметим, что в таблицах приведены также данные для определения коэффициентов и , о которых пойдет речь ниже.

Введя в формулу (2.2) W_t – удельную расчетную окружную силу , получим 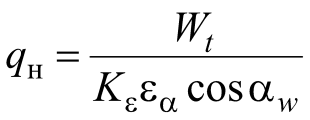Н/мм. (2.4)

 

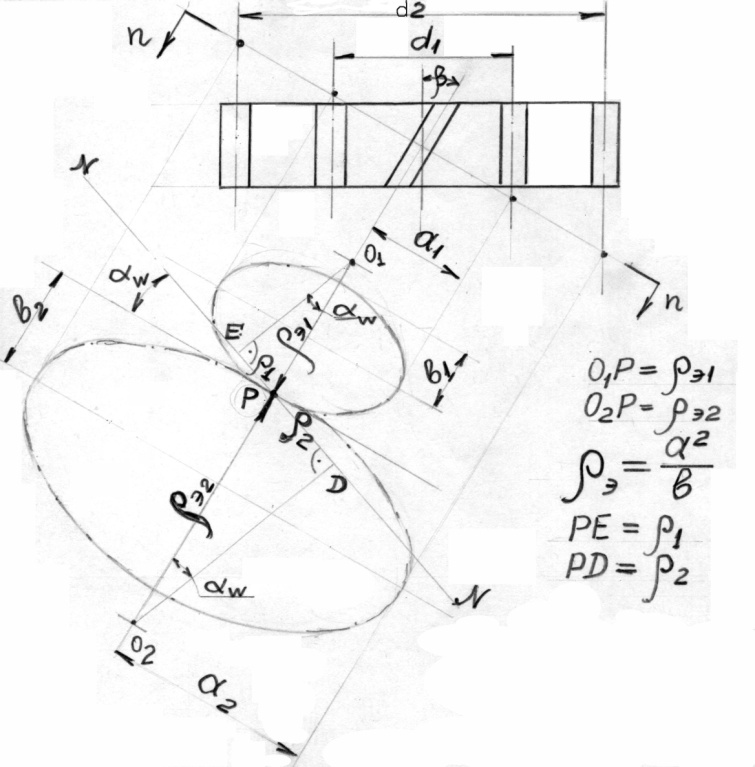
Рис. 12

Для определения приведенного радиуса кривизны , входящего в исходное уравнение 2.1, требуется решить два прямоугольных треугольника О1ЕР и О2DР из рис.12 при известных радиусах кривизны ρ _э1 и ρ _э2. В этих треугольниках за радиус кривизны шестерни и колеса ρ ₁ и ρ ₂ приняты отрезки от основания перпендикуляра, опущенного на линию зацепления N-N до полюса зацепления Р, в котором косозубые колеса заменены эквивалентными прямозубыми эллиптическими колесами. Таким образом

или мм.

Подставляя все полученные данные в исходное уравнение Герца (2.1), получим .

Заменив в знаменателе и введя обозначения:

– коэффициент, учитывающий форму сопряженных поверхностей зубьев, - коэффициент, учитывающий механические свойства материала зубчатых колес, и 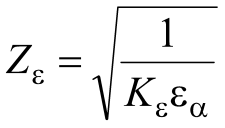- коэффициент, учитывающий суммарную длину линий контакта зубьев, получим формулу для проверочного расчета зубчатых колес на контактную выносливость

(2.5)

Как видно из формулы, контактное напряжение увеличивается при увеличении действия крутящего момента Т₁ и уменьшается при увеличении ширины 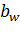, диаметра и угла наклона β зубчатых колес.

Коэффициент Z_H в среднем равен Z_H=2, 5. При отсутствии смещения режущего инструмента (х=0) и 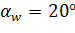пользуются формулой .

Коэффициент для стальных зубчатых колес при модуле упругост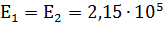и Мпа и .

При модуле упругости 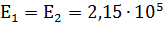Мпа значение .

Коэффициент для косозубых и шевронных зубчатых передач при 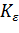> 0, 9 , где . При 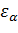=1, 2…1, 8 в среднем можно принять =0, 9.

 

Для проверочного расчета при действии максимальной нагрузки с целью предотвращения остаточных деформаций или хрупкого разрушения поверхностного слоя зубьев следует пользоваться формулой:

. (2.6)

 

Здесь Т_max – пиковый момент при пуске двигателя под нагрузкой. Находится из данных каталога на рыночные электродвигатели [3].

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Популярное:

1. B передачи выходного вала компоненты
2. I, Верхние передачи мяча двумя руками — 15 мин,
3. I. Предпосылки перехода к радикальным реформам
4. I.1. Основные предпосылки и механизмы развития речевой деятельности
5. II. Обучение верхней передаче двумя руками—40 мин.
6. II. Обучение верхней передаче—20 мин.
7. IV. Философские предпосылки гражданского права. Проблема личности и государства
8. Автоматическая коробка передач
9. Акт приёма-передачи базы данных
10. Алгоритм проектирования цилиндрических зубчатых передач
11. Аналоговые многоканальные системы передачи
12. АХ – это зависимость амплитуды выходного напряжения от амплитуды входного напряжения.