Воспользовавшись формулой Эйлера

(2.6)

запишем координаты комплекса амплитуды напряжения на осях Re и Im комплексной плоскости (рис. П2.3б):

(2.7)

Соотношение (2.7) показывает, что синусоидальная функция напряжения u(t) = = U_msin(wt + Y_u) это проекция вращающегося вектора на мнимую ось, другими словами, это мнимая часть (без j) комплексной амплитуды напряжения, так как

а косинусоидальная функция напряжения u(t) = U_mcos(wt + Y_u) есть проекция вращающегося вектора на действительную ось или действительная часть комплексной амплитуды напряжения, так как

Например, u = 10sin(wt + 45°) Û где В - комплексная амплитуда напряжения.

Поделив комплексную амплитуду напряжения U_mна , получим комлекс действующего значения напряжения или комплекс напряжения:

= (2.8)

По аналогии записывают комплексы ЭДС и тока , например,

i = 14, 1sin(314t - 30°) А Û I = A.

Переход от комплексов к синусоидальным функциям осуществляют следующим образом:

Û u(t) = U sin(wt + Y_u ), (2.9)

Û i(t) = I_m sin(wt + Y_i) и т. д.

П2.4. Формы записи комплексного числа, формулы перехода из одной формы записи в другую и алгебра комплексных чисел. Аналитически комплексное число А можно представить в трёх формах: в алгебраической A = a + jb, тригонометрической A = А(cosY_а + jsinY_а)и показательной A = (рис. П2.3а), т. е.

А = = А(cosY_a + jsinY_a) = a + jb, (2.10)

где А = |А|= иY_а= arctg - модуль и аргумент комплексного числа А; a = = Re[А] и b = Im[А] - действительная и мнимая части комплексного числа А.

Если модуль А = 1, получим формулу Эйлера:

В соответствии с (2.10) переход от алгебраической формы А = a ± jb к показательной осуществляют по формуле:

А = , (2.11)

а от показательной формы к алгебраической - через тригонометрическую:

А = = = a ± j b. (2.12)

Если действительная часть комплексного числа имеет знак минус, например, комплекс А =- a ± jb, то его аргумент определяют по формуле

Y_а = arctg(b/a) - p. (2.13)

Например,

Сложение и вычитание комплексных чисел проводят в алгебраическойформе:

A ± B = (a₁± ja₂) ± (b₁ ± jb₂) = (a₁ ± b₁) ± j(a₂ ± b₂). (2.14)

Чтобы сложить два комплексных числа, заданных в показательной форме, например , вначале их нужно преобразовать в алгебраическую форму согласно (2.12), а затем использовать соотношение (2.14).

У множение и деление комплексных чисел удобно проводить в показательной форме:

·при умножении комплексов A и B их модули перемножают, a аргументы суммируют:

; (2.15)

·при делении комплексов A и B их модули делят, а аргументы вычитают:

= . (2.16)

Если комплекс B = B = = то умножение вектора А на вектор B, т. е.

Рис. П2.4. Повороты вектора А при его умножении на ± j (а) и расположение комплексно-сопряженных векторов С и С* в комплексной плоскости (б)

Y_с

б)

-Y_с

-w

-jb

С*

Y_a

j²A = -A

p/2

а)

-jA

-p/2

равнозначно повороту вектора А на уголp/2 против хода часовой стрелки, а умножение вектора А на оператор –j=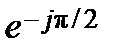

равнозначно его повороту на угол p/2 по ходу часовой стрелки(см. вектор -jA на рис.П2.4а).

Умножение же вектора A на оператор j²= -1 равнозначно повороту вектора А на угол±p (см. рис.П2.4а), т.е. получим противоположно направленный вектор –А:

j²A = j .

Если комплексная величина С^* (рис. П2.4б) отличается от комплекса С только знаком мнимой части, то её называют сопряжённым комплексом (это зеркальное отображение вектора С относительно оси действительных чисел Re). Итак, если

С = Се = С(cosY_c+ jsinY_c) = a + jb, то

С^*= Се = С(cosY_c - jsinY_c) = a - jb. (2.17)

П2.5. М етоды анализа цепей синусоидального тока. В основе расчёта цепей синусоидального тока лежат первый и второй законы Кирхгофа, записанные для мгновенных значений электрических величин. Руководствуясь компонентными уравнениями элементов схемы цепи:

и записав для неё уравнения законов Кирхгофа, получают систему интегрально-дифференциальных уравнений типа

причём правая часть этих уравнений содержит гармонические функции времени, а в левой части уравнений каждая синусоидально изменяющаяся величина (при заданной угловой частоте w) содержит два неизвестных параметра (амплитуду и начальную фазу).

Задача анализа линейной электрической цепи в установившемся режиме при гармоническом воздействии сводится к решению системы линейных дифференциальных уравнений с постоянными коэффициентами, правыми частями которых являются гармонические функции времени одной и той же частоты. Для решения этих уравнений используют метод векторных диаграмм (для анализа простейших схем обычно с одним источником питания), комплексный ( символический ) метод и реже метод переменных энергетического состояния цепи.

П2.5. Основы комплекснго (символическогой) метода анализа сложных схем цепей гармонического тока. При анализе установившихся процессов в сложной электрической цепи гармонические функции изображают комплексными числами, что позволяет перейти от интегрально-дифференциальных уравнений, составленных для мгновенных значений токов и ЭДС источников энергии, к алгебраическим уравнениям, составленным для комплексов токов и ЭДС.

При этом комплексными числами изображают не только гармонические ЭДС, токи и напряжения (см. П2, 3 и П2.4) но и параметры пассивных элементов цепи: резисторов, индуктивных катушек и конденсаторов. Решив систему комплексных алгебраических уравнений, составленных на базе законов Кирхгофа, метода узловых напряжений и др., рассмотренных при анализе цепей постоянного тока, находят комплексные амплитуды (или комплексы действующих значений) токов и напряжений ветвей цепи, а затем переходят кеё временным функциям.

Пассивный элемент электрической цепи характеризуется своим комплексным сопротивлениемZ_Э- комплексным числом, равным отношению комплекса напряжения на зажимах данного элемента к комплексу тока этого элемента, т.е.

= . (2.18)

При этом комплексное сопротивление (комплекс полного сопротивления):

· ветвис резистором: Z_R = U_R / I_R = R, т.е. вектор тока I_R в ветви с резистором совпадает по фазе с вектором напряжения U_R на его зажимах;

· ветвис индуктивной катушкой; Z_L = U_L / I_L = jX_L = X_L т.е. вектор тока I_L в ветви с индуктивной катушкой отстает по фазе от вектора напряжения U_L на его зажимах на угол, равный p/2;

· ветвис конденсатором: Z_С = U_С/ I_С = -jX_С= X_С т.е. вектор тока I_С в ветви с конденсатором опережает по фазе вектор напряжения U_С на его зажимах на угол, равный p/2;

· RL-ветви: Z = U / I = Z , где модуль комплекса сопротивления RL-ветви Z = , а его аргумент j = Y_u - Y_i = arctg(X_L/R) > 0 определяет фазовый угол отставания вектора тока I от вектора напряжения U_L на зажимах RL-ветви;

· RС-ветви: Z = U / I = Z , где модуль комплекса сопротивления RС-ветви Z = , а его аргумент j = Y_u - Y_i = - arctg(X_С/R) < 0 определяет фазовый угол опережения вектором тока I вектора напряжения U на зажимах RС-ветви;

· RLС-ветви: Z = U / I = Z , где модуль комплекса сопротивления RLС-ветви Z = , а аргумент j = Y_u - Y_i = arctg[(X_L- X_C)/R] определяет фазовый сдвиг между векторами напряжения U и тока I на зажимах ветви: при X_L > X_C вектор тока отстает по фазе от вектора напряжения на угол j, при X_L < X_C вектор тока опережает по фазе вектор напряжения на угол j, а при X_L = X_C вектор тока совпадает по направлению в комплексной плоскости с вектором напряжения.

Величину, обратную комплексному сопротивлению Z, называют комплексной проводимостью Y последовательной RLC-ветви, т. е.

(2.19)

где g = и = b_L- b_C - активная и реактивная проводимостицепи; b_L= и b_C = - индуктивная и ёмкостная проводимости RLC-ветви.

Итак, комплексная (полная) проводимость RLC-цепи

Y = g - j(b_L- b_C) = g - jb , (2.20)

где и j = arctg - модуль и аргумент комплексной проводимости цепи.

П2.6. Закон Ома и законы Кирхгофа в комплексной форме. Для ветви с пассивнымиэлементами при совпадении условно положительных направлений тока и напряжения выражение закона Омаимеет вид

, (2.21)

где Z = Ze^j^j - комплекс сопротивления ветви.

Если j> 0, то ток отстаёт по фазе от напряжения, при j < 0 ток опережает по фазе напряжение.

Так как полная комплексная проводимость Y = 1/Z, то ток

I = UY = UYe . (2.22)

Запишем обобщённый закон Ома для ветвисn последовательно соединёнными источниками напряжения и пассивными элементами:

(2.23)

где Е_k и U - комплекс k-й ЭДС и комплекс напряжения на зажимах ветви; при этом знак плюс записывают при совпадении направлений ЭДС и напряжения c направлением токаветви, а знак минус - при их противоположном направлении.

Первый закон Кирхгофа(1ЗК) гласит, что в любом узле комплексной схемы замещения цепи алгебраическая сумма комплексов токов равна нулю, т. е.

. (2.24)

Условимся комплексы токов, направленные к узлу, записывать со знаком плюс, а комплексы токов, направленные от узла, записывать со знаком минус.

Второй закон Кирхгофа (2ЗК) гласит, что в любом контуре схемы цепи алгебраическая сумма комплексов ЭДС равна алгебраической сумме комплексов напряжений на пассивных элементах этого контура, т. е.

(2.25)

где (n) и (m) - число ЭДС и пассивных элементов в выбранном контуре.

Комплексы ЭДС и комплексы напряжений (токов) на пассивных элементах контура записывают со знаком плюс, если их направления совпадают с направлением обхода контура.

Пример П2.1. Составить необходимое число уравнений методом законов Кирхгофа относительно неизвестных комплексов токов ветвей (I₁, I₂ и I₃) схемы цепи (рис. П2.5).

-jX_C₁

R₂

R₃

jX_L₂

-jX_C₃

Рис. П 2.5

I₂

I₁

I₃

Решение. В соответствии с алгоритмом метода законов Кирхгофа:

1. Выбираем направления комплексов токов ветвей и обозначаем их стрелками на схеме (см. рис. П2.5).

2. Уточняем число узлов (У = 2) и ветвей (В = 3) схемы цепи с неизвестными токами.

3. Составляем уравнение по 1ЗК для узла 1:

4. Выбираем независимые контуры и направление обхода контуров по часовой стрелке. В нашем упражнении имеется два независимых контура (левый и средний).

Внимание! Ветвь с заданным комплексом тока J источника тока в уравнениях, составляемых по 2ЗК, не учитывается.

Запишем уравнения по 2ЗК (для независимых контуров):

Пример П2.2. Рассчитать схему цепи с одним источником напряжения (рис. П2.6a) со смешанным соединением ветвей методов преобразования (свертывания) схемы и с помощью правила делителя тока. Цепь подключена к источнику синусоидального напряжения, комплекс которого U.

I₃

-jX_C₁

R₂

R₃

jX_L₂

-jX_C₃

Рис. П2.6. Расчетная схема (а) и векторная диаграмма напряжений и токов (б) цепи

I₂

I₁

U₂

U₁

U₂

U₁

j₃

I₃

I₂

I₁

j₂

б)

Решение. 1. Зашишем комплексы сопротивлений ветвей:

, ,

2. Комплекс входного сопротивления Z = Z₁ + .

3. Комплекс входного тока цепи I₁= .

4. Комплексы токов ветвей определим, воспользовавшись правилом делителя тока::

5. Комплексы напряжения ветвей:

Векторная диаграмма токов и напряжений цепи представлена на рис. П2.6б, при этом

П2.7. Комплексная мощность цепи синусоидального тока. Комплексной мощностью цепи называют комплексное число S, модуль которого равен полной мощности S = UI цепи, а аргумент - углу сдвига фаз j = Y_u - Y_i между током и напряжением на её входе, т.е.

S = Se ^j^j = UIe ^j⁽^Y^u^-^Yⁱ⁾ = Ue ^j^Y^uIe^-^Yⁱ= U , ( 2.26)

т.е. комплексная мощность цепи равна произведению комплекса напряжения U на входной комплексно-сопряжённый ток

Переходя от показательной формы записи S к тригонометрической

S = Scosj + jSsinj,

устанавливаем, что действительная часть комплексной мощности равна активной мощности цепи

Р = Re[S] = Scosj. (2.27)

Мнимая часть комплексной мощности S представляет собой реактивную мощностьцепи

Q = Im[S] = Ssinj. (2.28)

С учётом (2.27) и (2.28) выражение (2.76) можно записать следующим образом:

S = P + jQ = . (2.29)

Итак, комплексная мощность S представляет собой комплексное число, действительная часть которого равна активной мощности цепи P, а мнимая - реактивной Q, причём если перед символом j стоит знак «плюс», то это реактивная индуктивная мощность +Q_L, а если знак «минус» - реактивная ёмкостная мощность -Q_С.

Пример П2.3. Рассчитать полную, активную и реактивную мощности цепи, комплексы тока и напряжения на зажимах которой U = 10e^j³⁰^°B и I = 2e^-^j⁴⁵^°A.

Решение. 1. Комплексно-сопряжённый ток = 2e^j⁴⁵^°A.

2. Комплексная мощность S = U = 10e^j³⁰^°× 2e^j⁴⁵^° = 20e^j⁷⁵^° В× А.

3. Активная мощность Р = Scosj = 20cos75° » 5, 2 Вт.

4. Реактивная мощность Q = Q_L = Ssinj = 20sin75° » 19, 3 вар.

П2.8. Баланс мощностей в цепи синусоидального тока. Из закона сохранения энергии следует, что сумма мгновенных мощностей, отдаваемых всеми источниками цепи, должна быть равна сумме мгновенных мощностей, потребляемых всеми приёмниками энергии.

= , (2.30)

где n и m - число источников и приёмников энергии в цепи.

Заметим, что потребляется и отдаётся не мощность, а электрическая энергия.

Уравнение (2.30) называют уравнением (условием) баланса мощностей.

В цепях синусоидального тока рассматривают баланс комплексных, активных и реактивных мощностей.

Условием баланса комплексных мощностей является соотношение, аналогичное (2.30):

. (2.31)

Для практических расчётов условие баланса комплексных мощностей цепи представляют в следующем виде:

(2.32)

при этом слагаемое, стоящие в левой части (2.32), берется со знаком «плюс», если совпадают направления тока I_k и ЭДС Е_k источника напряжения. В противном случае эти слагаемые берут со знаком «минус».

Из условия баланса комплексных мощностей следуют условия баланса активных и реактивных мощностей:

· активная мощность, отдаваемая всеми источниками энергии, равна активной мощности всех её потребителей (расходуемая в резистивных элементах цепи):

(2.33)

· реактивная мощность всех источников равна реактивной мощности всех потребителей (она циркулирует между источниками энергии и её потребителями):

(2.34)

где R_k и jХ_k = jХ_Lk - jХ_С_k - действительная и мнимая части комплексного сопротивления k-го пассивного элемента.

I₃

jX_L₁

R₂

jX_L₂

-jX_C₃

Рис. П2.7. Расчетная схема цепи

I₂

I₁

U₂

U₁

Пример П2.4. Для цепи (рис. П2.7) с параметрами: U = 10e^j⁴⁵ B, jX_L₁= j2, 5 Ом, R₂= 4 Ом, jX_L₂= j3 Ом, -jX_C₃= -j5 Ом рассчитать комплексы напряжений и токов ветвей. Результаты расчёта проверить посредством составления баланса мощностей.

Решение. 1. Определим комплексы сопротивлений ветвей:

2. Комплекс входного сопротивления

Z = Z₁ +

3. Комплекс входного тока I = I₁ = U/Z = 20e^j⁴⁵^°/5 = 4e^j⁴⁵^° A.

4. Комплексы токов ветвей разветвления:

5. Комплексы напряжений ветвей:

6. Комплексная мощность, отдаваемая источником,

должна быть равна комплексной мощности, потребляемой приёмниками:

Таким образом, условие баланса комплексных мощностей с допустимой погрешностью выполнено. При этом активная мощность источника энергии и приёмников Р_ист » Р_пр = 80 Вт, а реактивные мощности Q_ист» Q_пр = 0.

Задание 3

⇐ Предыдущая 1 2 3 4 567 8 Следующая ⇒