П2. Анализ и расчёт однофазной цепи переменного тока
(см. задание КР6-2)
П2.1. Основные определения. Токи, напряжения и ЭДС, значения которых периодически изменяются во времени по синусоидальному закону, называют синусоидальными (гармоническими), нередко (не совсем точно) переменными. По сравнению с постоянным током синусоидальный имеет ряд преимуществ, в частности, производство, передача и использование электрической энергии наиболее экономичны при синусоидальном токе; в цепях синусоидального тока относительно просто преобразовывать форму напряжения, а также создавать трёхфазные системы напряжения. Синусоидальные токи широко используют в радио-, связной и контрольно-измерительной технике и в других областях.
Синусоидальную величину, например напряжение, можно задать с помощью вещественной функции времени
, (2.1)
| Рис. П2.1. Временная (а) и векторные диаграммы напряжения и тока в прямоугольной (б) и в комплексной (в) плоскостях
|
где
u или
u(
t) - мгновенное значение напряжения;
Um и
– амплитуда и фаза синусоидальной функции, или в виде
временнó й (
а)или
векторной диаграммы в прямоугольной
х-у (
б) или в комплексной Re-Im (
в) плоскостях (рис. П2.1).
При построении временнó й диаграммы за аргумент синусоидальной функции, например напряжения u(t), принимают время t (чему соответствуют период T и начальное время t0 = Yu/w) или угол wt (чему соответствуют период wT = 2p и начальная фаза Yu в радианах) (см. рис. П2.1а). Однако для большей наглядности угол Yu часто выражают в градусах. Тогда аргумент wt также переводят в градусы (напомним, что 1 рад » 57, 3°). В этом случае период wT составляет 360°.
Представление синусоидальных функций при помощи векторов, вращающихся в направление против хода часовой стрелки, позволяет наглядно показать количественные и фазовые соотношения между электрическими величинами в цепях синусоидального тока, и широко используется при анализе электромагнитных процессов и выводе основных соотношений между электричекими величинами.
Векторная диаграмма (ВД) - это совокупность векторов ЭДС, напряжения и тока, изображающих в плоскости синусоидально изменяющиеся с одной и той же частотой электрические величины. В прямоугольной системе координат (оси x и y) эти векторы будем обозначать соответствующими прописными буквами, подчёркнутыми снизу: вектор амплитуды напряжения Um, вектор амплитуды тока Im (рис. П2.1б). Длина, например вектора амплитуды тока Im, должна быть равна (в соответствующем масштабе) амплитуде тока Im, а угол наклона к оси абсцисс - его начальной фазе Yi. В этом случае проекция вектора тока Im на ось ординат равна мгновенному значению тока в момент времени t = 0, т. е. i(0) = ImsinYi, где Yi – начальная фаза тока (см. рис. П2.1б).
Угол сдвига фаз j = Yu - Yi между напряжением и током на входе цепи или на неразвлетленном ее участке при вращении векторов остаётся неизменным, поэтому при построении векторной диаграммы векторы обычно изображают не вращающимися, а неподвижными для момента времени t = 0 (wt = 0). Знак угла j на векторных диаграммах определяют по направлению его отсчетаот вектора тока Im к вектору напряжения Um: если указанное направление угла j совпадает с направлением частоты w вращения векторов на ВД, то угол j берётся со знаком «плюс» (рис. П2.1б), если направление отсчёта угла j совпадает с направлением хода часовой стрелки, то угол j берётся со знаком «минус»..
Время, в течение которого вектор напряжения (тока) совершает один оборот, называют периодом синусоидального напряжения (тока), а величину, обратную периоду Т, определяющую число периодов в секунду – циклической частотой[Гц], т.е.
(2.2)
Частота промышленных сетей в России 50 Гц, в США и Японии – 60 Гц, корабельных сетей – 250 Гц, сетей летательных аппаратов –400 Гц, радиотехнических устройств – сотни кило- и мегагерц, гаджетов – единицы гигагерц.
Величину, определяющую число периодов в интервале времени, равном 2p, называют угловой частотойw[рад/с].
Соотношение между периодом T, угловой w и циклической f частотами:
(2.3)
П2.2. Средние и действующие значения синусоидальных функций. Так как среднее значениегармонического тока 
за период T равно нулю, то под средним значением тока i(t) понимают среднее в интервале времени T/2 (рис. П2.2а), т.е.:
(2.4)
| Рис. П2.2. К определению среднего (а) и действующего (б) значений гармонического тока i(t)
|
Таким образом,
среднее значение синусоидального тока
Iср равно его амплитудному значению
Im, умноженному на 2/p.
Аналогично определяют средние значения напряжения и ЭДС:
Действующий ток (напряжение) - это основной эксплуатационный параметр цепей синусоидального тока, так как тепловое действие тока и механическая сила взаимодействия проводников с токами пропорциональны квадрату тока (произведению токов). Шкалы большинства измерительных приборов (амперметров, вольтметров) проградуированы на эти значения.
Действующее значение (действующий ток) это среднеквадратичное значение синусоидального тока за время Т (рис. П2.2б):
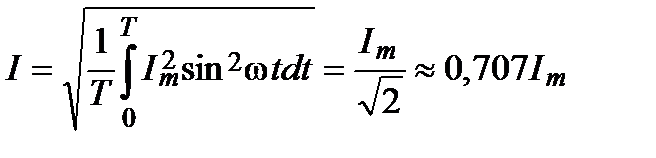, (2.5)
т. е.действующий ток равен амплитуде, делённой на 
.
Аналогично определяют действующие значения напряжения u(t) и ЭДС e(t):
, 
.
Популярное:
