Исчисление предикатов со схемами аксиом

Исчисление предикатов со схемами аксиом [16] надстравивается над соответствующим исчислением высказываний. К пропозициональным аксиомам добавляются
кванторные аксиомы и правила вывода. Это и есть исчисление предикатов первого порядкасо схемами аксиом. К перечисленным аксиомам добавляются следующие:

CA11. 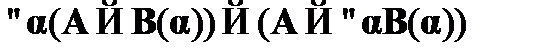– схема введения квантора общности в консеквент;

CA12. – схема введения квантора существования
в антецендент ( A не содержит свободно α );

CA13. – схема исключения квантора общности;

CA14. 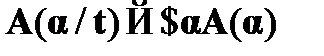– схема введения квантора существования.

Что касается правил вывода, то к modus ponens системы исчисления высказываний со схемами аксиом добавляется правило генерализации:

.

Доказательство в исчислении предикатов со схемами аксиом. Понятие доказательства, заданное при построении высказываний со схемами аксиом, без изменений переносится и в исчисление предикатов первого порядка со схемами аксиом.

Рассмотрим пример доказательства теоремы (закон подчинения):

(1) 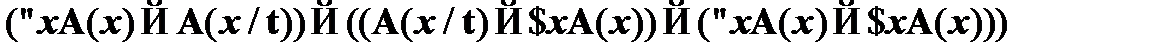– транзитивность (из приведенного выше доказательства закона транзитивности);

(2) – схема аксиом CA13;

(3) 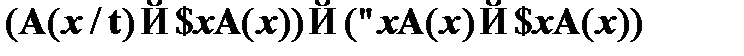– modus ponens к (1), (2);

(4) – схема аксиом CA14;

(5) – modus ponens к (3), (4).

Как мы уже успели убедиться, доказательство значительно упрощается, если в системе исчисления предикатов со схемами аксиом доказуема метатеорема дедукции. Прежде чем приступать к доказательству, необходимо сформулировать понятие логического вывода для логики предикатов первого порядка.

Выводом формулы B из посылок в аксиоматическом исчислении предикатов называют непустую конечную последовательность формул , в которой последняя формула графически совпадает с формулой B ( ). Данная последовательность должна удовлетворять условиям: каждая в последовательности должна быть или одной из посылок , или аксиомой, или получена из предыдущих формул по правилу modus ponens или по правилу генерализации, которое применялось к переменным, не входящим свободно в посылки.

Теперь можно сформулировать теорему дедукции для исчисления предикатов первого порядка со схемами аксиом: если из некоторого множества формул Г
и формулы A выводима формула B и правило генерализации не применялось к свободным переменным посылки A , то из множества формул Г выводима формула 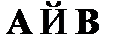.Схематически это выглядит так:

.

Доказательство теоремы дедукции для исчисления предикатов. Система
исчисления предикатов первого порядка со схемами аксиом является надстройкой над соответствующим исчислением высказываний. Таким образом, все индуктивные шаги, которые имели место при доказательстве теоремы дедукции для исчисления высказываний со схемами аксиом, сохраняются полностью. Однако к доказательству добавляется еще один индуктивный шаг, связанный с правилом генерализации.

Предположим, что формула , содержащаяся в выводе , получена по правилу генерализации, т. е. . Генерализация применялась по переменной α, которая не является свободной в устраняемой посылке A. Нам необходимо показать, что свойство будет выполняться для формулы .

В силу того что предшествуют формуле , ее номер меньше n, а значит, для нее имеет место свойство , т. е. . Следовательно, необходимо показать, что имеет место 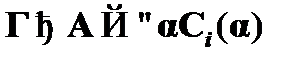. С этой целью рассмотрим последовательность формул:

(1) – выполнимость свойства для формулы ;

(2) – правило генерализации к (1);

(3) – частный случай CA11;

(4) – modus ponens к (3), (2).

Таким образом, по индуктивному допущению мы имеем: . Приведенная последовательность показывает, что имеет место и выводимость . Применив сечение, мы можем показать, что имеет место выводимость 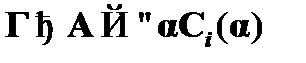. Тем самым индуктивный шаг доказан, а значит, доказана справедливость теоремы дедукции для исчисления предикатов первого порядка со схемами аксиом.

Пример 5. Рассмотрим пример применения теоремы дедукции. Докажем теорему 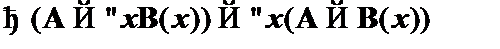, где A не содержит x свободно:

(1) 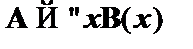– посылка;

(2) A – посылка;

(3) – modus ponens к (1), (2);

(4) – частный случай CA12;

(5) – modus ponens к (4), (3);

(6) 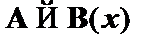– теорема дедукции к (2)–(5);

(7) – правило генерализации к (6);

(8) – теорема дедукции к (1)–(7).

Данный пример требует пояснений. Применение теоремы дедукции на шаге (6) объясняется тем, что правило генерализации на шагах (1)–(5) не применялось. На шаге (7) правило генерализации было применено к переменной x. Эта переменная связана в формуле , а в формуле A не содержится свободно. Таким образом, в посылке переменная x не содержится свободно. Это и позволяет применить теорему дедукции на последнем шаге и получить утверждение о доказуемости .

⇐ Предыдущая78910111213141516Следующая ⇒

Поделиться:

Популярное:

1. Аксиома о потенциальной опасности деятельности
2. Аксиоматический способ построения теории
3. Аксиоматическое исчисление высказываний
4. Аксиоматическое определение вероятности
5. Аксиоматическое определение вероятности.
6. Аксиомы линейного пространства
7. Анализ математических аксиом
8. Виды формул в классической логике предикатов первого порядка
9. Дж. Хоманс выделяет шесть аксиоматических положениях (постулатах) теории обмена.
10. Дифференциальное исчисление функции одной переменной
11. Интерпретация и логические отношения в логике предикатов