Виды формул в классической логике предикатов первого порядка

⇐ ПредыдущаяСтр 10 из 32Следующая ⇒

Понятие логического закона в логике предикатов первого порядка может быть конкретизировано следующим образом: формула A является общезначимой формулой (логическим законом) в том и только в том случае, если A принимает значение «истина» в каждой из возможных реализаций языка 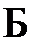и при каждом приписывании значений предметным переменным . Данное определение может быть выражено посредством метаязыковой записи: 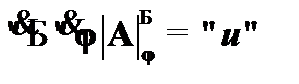. Утверждение « A общезначимо» записывается как « ».

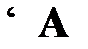Формула A является опровержимой, если и только если существует реализация языка 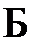и существует функция , при которых A принимает значение «ложь», т. е. .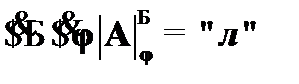

Формула A выполнима, если и только если существует реализация языка 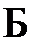и функция приписывания значений предметным переменным , при которых A принимает значение «истина», т. е. .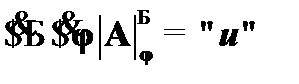

Формула A является невыполнимой (тождественно-ложной) тогда и только тогда, когда она принимает значение «ложь» в каждой реализации 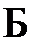и при любом , т. е. .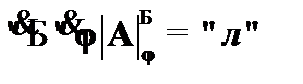

Приведем схемы общезначимых формул (законов) логики предикатов первого порядка:

1. Взаимовыразимость кванторов:

;

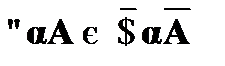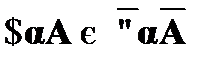2. Образование контрадикторных противоположностей (законы отрицания кванторов):

;

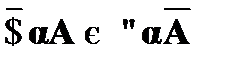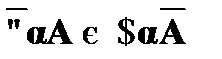3. Закон подчинения (связь квантора общности и квантора существования):

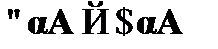– закон подчинения.

4. Законы пронесения кванторов:

;

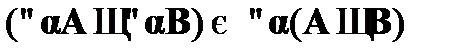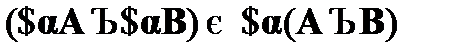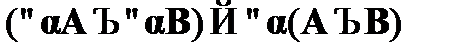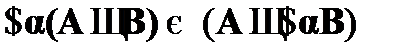, если 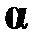не свободна в А;

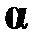, если не свободна в A;

;

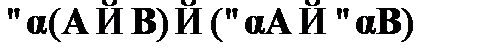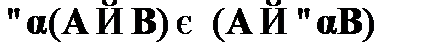, если 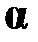не свободна в A;

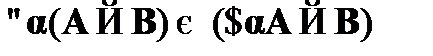, если 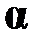не свободна в B;

;

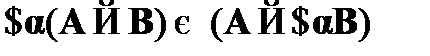, если 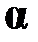не свободна в A;

, если 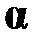не свободна в B,

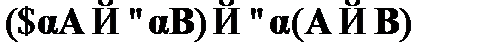5. Законы перестановки кванторов:

;

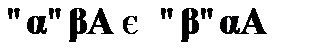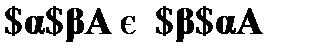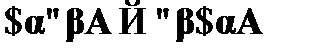6. Закон удаления квантора общности:

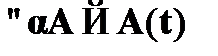, где A ( t ) – результат подстановки вместо всех свободных вхождений переменной α в формулу A терма t.

7. Закон введения квантора существования:

, где A ( t ) – результат подстановки вместо всех свободных вхождений переменной α в формулу A терма t.

8. Закон непустоты предметной области:

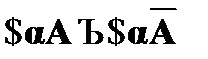Понятие модели. В классической логике предикатов первого порядка имеются формулы, которые выполнимы, но не тождественно-истинны, т. е. они оказываются истинными в некоторых возможных высказываниях. Представителей конкретных наук интересуют лишь такие возможные реализации языка, в которых любое утверждение этих наук является истинным. Такие реализации именуются моделями.

Возможная реализация 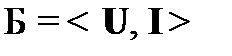называется моделью формулы A, если формула A принимает значение «истина» в этой реализации при любом приписывании φ значений индивидным переменным, т. е. .

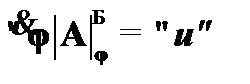Возможная реализация 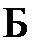называется моделью множества формул Г, если 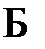является моделью для каждой формулы .

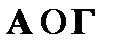Как и в пропозициональной логике, фундаментальными логическими отношениями в логике предикатов первого порядка являются отношения совместимости по истинности, совместимости по ложности и логического следования. Пусть Г – произвольное множество формул.

Совместимыми по истинности называют такие формулы из Г, если и только еслисуществуют реализации 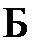и приписывание значений предметным переменным φ, при которых каждая формула принимает значение «истина». В противном случае эти формулы являются несовместимыми по истинности.

Если и только если существуют реализации 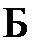и приписывание значений предметным переменным φ, при которых каждая формула из Г принимает значение «ложь», то такие формулы из Г совместимы по ложности. В противном случае такие формулы несовместимы по ложности.

Логическое следование между множеством формул Г и формулой B ( Г 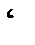B ) имеет место в том случае, если не существует такой реализации 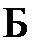и приписывания значений предметным переменным φ, при которых каждая формула из Г принимает значение «истина», а формула B – «ложь».

Законов логики предикатов первого порядка и понятия логического следования недостаточно для анализа рассуждений. Практически важным является установление процедуры, которая бы позволяла показать, что некоторая формула A действительно является законом данной логической теории и что из формул A₁, A₂, …, A_n в этой теории действительно следует формула B. В отличие от пропозициональной логики, дефиниции логического закона и логического следования в логике предикатов не содержат алгоритма решения вопросов об общезначимости произвольной формулы A и наличии отношения логического следования между формулами 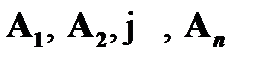и B. Для того чтобы показать, что имеет место отношение логического следования 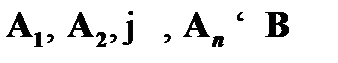, нужно рассмотреть все возможные реализации 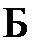и возможные распределения значений предметных переменных и удостовериться, что среди них нет таких, когда 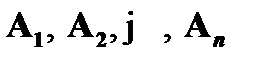принимали бы значение «истина», а B – значение «ложь». Однако это невозможно, так как количество всех реализаций 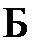и приписываний φ невозможно в силу того, что их число бесконечно. Никакого алгоритма не существует в принципе. Следовательно, классическая логика предикатов неразрешима.

Но в классической логике предикатов первого порядка разработан ряд методов, применение которых позволяет упростить процедуру обоснования общезначимости формул и наличия следования между формулами языка логики предикатов. Одним из таких методов и является метод аналитических таблиц [12].

Тезисы об общезначимости некоторой формулы A или о наличии логического следования 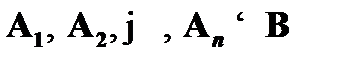обосновывается посредством рассуждения от противного. Это предполагает, что первым шагом доказательства является принятие антитезиса в качестве допущения. Таким образом, для обоснования тезиса « 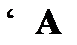» необходимо показать, что антитезис « 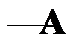» приводит к противоречию. Для обоснования тезиса
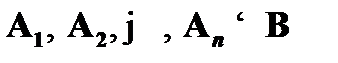« » демонстрируют, что если допустить истинность 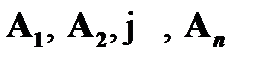и ложность B, то с необходимостью будет получено противоречие. Рассуждение от противного оформляется в виде аналитической таблицы. Данный метод также может быть использован применительно к формулам логики высказываний. В последнем случае метод аналитических таблиц является разрешающей процедурой.

Анализ некоторой формулы A начинается с предположения, что при некотором распределении истинностных значений по ее пропозициональным переменным формула A ложна. Предположение об истинности или ложности формулы отмечается с помощью добавления символов T и F перед формулой (для формулы A – TA и FA соответственно). Такие формулы называются отмеченными.Дальнейший анализ формул осуществляется по правилам, которые соответствуют семантическим условиям истинности и ложности пропозициональной логики и логики предикатов первого порядка.

В множестве отмеченных формул выделяют цепи, под которыми понимают последовательность вхождений отмеченных формул, начинающуюся с самой верхней формулы таблицы до одной из самых нижних формул. Место расщепления цепи помечают двумя линиями – горизонтальной и вертикальной.

Таблица, соответствующая первому шагу рассуждения от противного, содержит одну цепь отмеченных формул и выражает исходные допущения данного рассуждения, т. е. антитезис. Если тезисом является « », то эта цепь начинается с отмеченной формулы FA. Данная формула представляет собой корень дерева. Если тезисом является « 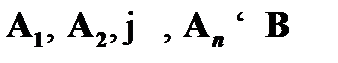», то начальная цепь будет состоять из отмеченных формул 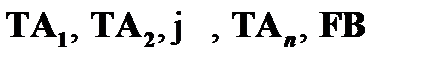и корнем дерева будет являться формула TA₁. Дальнейшие шаги построения аналитической таблицы осуществляются с помощью правил, которые зачастую именуются правилами редукции. Эти правила применяются к отмеченным формулам, находящимся в некоторой цепи таблицы. Их применение приводит либо к продолжению построения данной цепи, либо к ее расщеплению на две самостоятельные цепи.

Задача, которая решается построением аналитической таблицы, состоит в получении такой таблицы, каждая цепь которой содержит утверждение как об истинности, так и ложности некоторой формулы C, т. е. в каждой цепи должны присутствовать отмеченные формулы TC и FC. Если этот результат достигнут, то соответствующая формула считается общезначимой.

Правила редукции . Каждое правило обозначается посредством символов T и F
с нижним индексом, который указывает на пропозициональную связку или квантор. Ниже представлены правила редукции для пропозициональной логики.

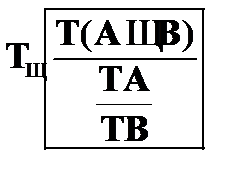
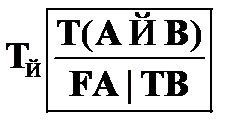
Правило 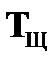предполагает, что при наличии в цепи отмеченной формулы , которая согласно определению конъюнкции может быть истинной в том и только в том случае, если истинными являются ее подформулы A и B, в эту же цепь можно поместить две отмеченные формулы – TA и TB.

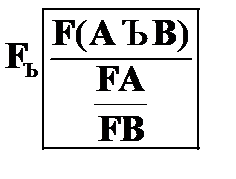
Правило 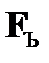позволяет при наличии в цепи отмеченной формулы 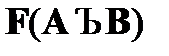поместить в эту же цепь отмеченные формулы FA и FB. Применение этого правила связано со свойствами дизъюнкции, которая может быть ложной только при одновременной ложности ее подформул.

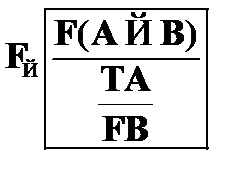
Правило 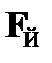основано на свойствах импликации. Согласно табличному определению импликация ложна только в случае, если истинен антецендент и ложен консеквент. В соответствии с этим данное правило позволяет в случае наличия в цепи отмеченной формулы 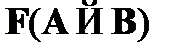поместить в эту же цепь отмеченные формулы TA и FB.

Правила 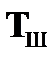и 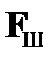основаны на свойствах отрицания, т. е. они позволяют при наличии в цепи отмеченных формул или поместить в эту же цепь соответственно формулы 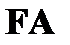или .

Правило 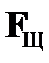основано на свойствах конъюнкции. В соответствии с определением конъюнкция ложна в случае, если ложен хотя бы один из ее членов. Если в некоторой цепи содержится отмеченная формула , то исходная цепь расщепляется и в одну ветку помещается отмеченная формула 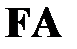, а в другую – .

Правило 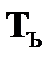предполагает, что согласно свойствам дизъюнкции при наличии в цепи отмеченной формулы 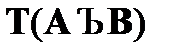она распадается на две ветки, в одну из которых помещается отмеченная формула , а в другую – .

Правило 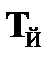предполагает, что при наличии в некоторой цепи отмеченной формулы 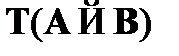она расщепляется на две подцепи, в одну из которых входит формула 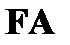, а в другую – .

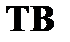Необходимо помнить, что в случае расщепления подцепи содержат все отмеченные формулы той цепи, в которой находилась исходная отмеченная формула.

Ниже представлены правила редукции для формул, содержащих кванторы:

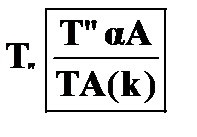
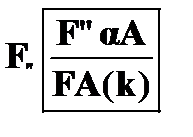
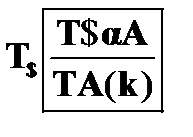
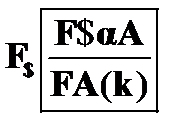
Правило 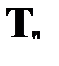применяется в том случае, если в некоторой цепи имеется отмеченная формула вида 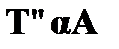. Формула истинна, если и только если любой индивид предметной области удовлетворяет условию A. Это означает, что истинной оказывается
также любая формула вида A(k), которая представляет собой результат подстановки вместо всех свободных вхождений α в A произвольного замкнутого терма k. Замкнутым термом k может быть только уже содержащийся в отмеченных формулах данной цепи замкнутый терм, а если таковых нет в цепи, то можно взять любую индивидную константу. Это правило редукции является глобальным, т. е. оно может применяться неоднократно для того, чтобы повторным применением получать утверждения об истинности A ( k₁ ), A ( k₂ ), … для замкнутых термов, уже содержащихся в аналитической таблице и отличных от терма k.

Правило 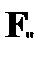. Если в некоторой цепи имеется формула 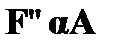, то это равносильно утверждению о ложности . Таким образом, утверждается, что существует объект, который не удовлетворяет условию A. Значит, если ввести в качестве имени этого объекта новую, не встречающуюся в отмеченных формулах цепи предметную константу k, то формула A ( k ) оказывается ложной. Это позволяет поместить в данную цепь отмеченную формулу .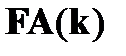

Правило 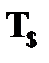. Пусть в анализируемой цепи содержится отмеченная формула 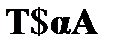, представляющая собой утверждение об истинности 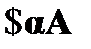. Истинность такой формулы означает существование объекта, возможно единственного, удовлетворяющего условию A. В качестве имени этого объекта вводится новая, не встречающаяся в отмеченных формулах цепи предметная константа k. Таким образом, A ( k ) истинно в силу того, что k удовлетворяет условию A.

Правило 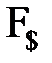. Если в некоторой цепи содержится отмеченная формула 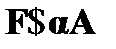, то это говорит о ложности 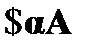. Ложность этой формулы означает, что ни один индивид предметной области не удовлетворяет условию A. Поэтому эта же цепь пополняется отмеченной формулой вида 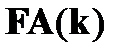, где k удовлетворяет тем же самым условиям, которые были сформулированы для правила .

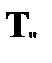Сформулировав правила редукции, мы можем конкретизировать основные понятия метода аналитических таблиц. Аналитической таблицей является конечное или бесконечное дерево отмеченных формул, получаемое из начальной цепи применением правил редукции.

Цепь аналитической таблицы называется замкнутой, если в ее составе встречается две противоречащие друг другу отмеченные формулы – TC и FC. В соответствии с этим в замкнутой аналитической таблице каждая цепь является замкнутой.

Следовательно, формула A общезначима, если и только если существует замкнутая аналитическая таблица, начальная цепь которой начинается с отмеченной формулы FA. Из множества формул A₁, A₂, …, A_n логически следует формула B тогда и только тогда, когда существует замкнутая аналитическая таблица, начальная цепь которой начинается с отмеченных формул TA₁, TA₂, …, TA_n и FB.

Следует помнить, что правила редукции всегда применяются к тем логическим константам, содержащимся в формуле A, идущей после отметки T или F, которые являются в ней главными знаками.

Правила подразделяются на пропозициональные и кванторные. При этом в построении аналитической таблицы сначала применяются пропозициональные правила, не ведущие к расщеплению цепей, а затем кванторные правила редукции.

Среди кванторных правил редукции рекомендуется в первую очередь применять правила 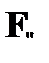и 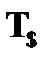, которые требуют введения новых предметных констант, и только потом правила 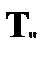и 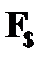, которые не содержат ограничений на терм k, подставляемый вместо подкванторной переменной.

Расщепляющие правила следует применять в последнюю очередь, только после того, как применены все нерасщепляющие пропозициональные и кванторные правила.

Пример 1. Необходимо обосновать выводимость вида . Согласно методу аналитических таблиц в первую очередь мы должны выделить две отмеченные формулы:
и 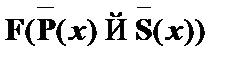. Эти формулы помещаются в начало цепи. Сама цепь примет следующий вид:

(1)
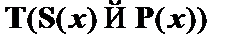
(2)
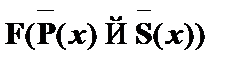
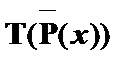
(3)	– из (2) по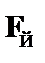
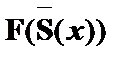
(4)	– из (2) по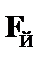
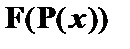
(5)	– из (3) по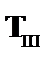
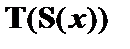
(6)	– из (4) по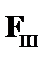
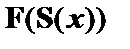
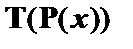
(7)		– из (1) по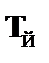

Как видно из приведенной аналитической таблицы, на седьмом шаге цепь расщепляется. При этом в каждой цепи таблицы имеются отмеченные формулы, противоречащие друг другу. В левой цепи – это 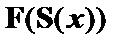и 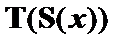, а в право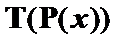й – и 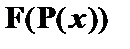. Таким образом, аналитическая таблица замкнута. В данном случае имеет место логическое следование вида .

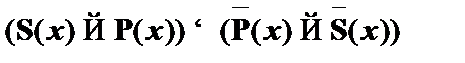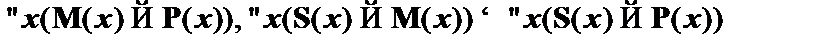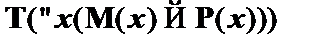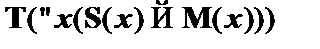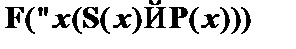Пример 2. Возьмем пример, содержащий квантифицированные формулы. Необходимо обосновать выводимость вида . Для начала введем предположение о том, что , и . Поместим данные отмеченные формулы в начало цепи. Аналитическая таблица будет иметь вид:

(1)
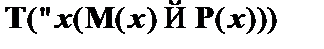
(2)
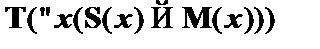
(3)
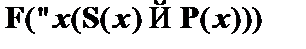
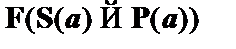
(4)	– из (3) по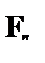
(5)	– из (1) по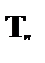
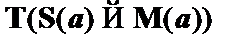
(6)	– из (2) по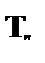
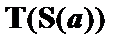
(7)	– из (4) по
(8)	– из (4) по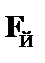
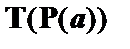
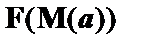
(9)		– из (5) по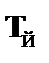
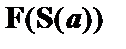
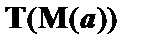
			– из (6) по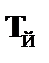

Как видно из приведенного примера, левая цепь таблицы является замкнутой в силу того, что в ней присутствуют две противоречащие друг другу отмеченные формулы и 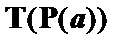. Средняя цепь замкнута, так как в ней имеются отмеченные формулы 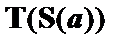и 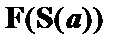. В правой цепи имеются формулы 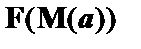и 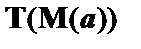, а значит, она тоже замкнута. Таким образом, все цепи аналитической таблицы замкнуты, следовательно, и вся таблица является замкнутой. Это позволяет сделать вывод о наличии отношения логического следования между посылками и выводом.

⇐ Предыдущая 5 6 7 8 91011 12 13 14 Следующая ⇒